29. Запишем уравнение Беллмана (4.4)

.

Перепишем это уравнение следующим образом:

. (4.11)

Обозначим .

Тогда (4.11) приводится к виду

, (4.12)

где . (4.13)

В классическом вариационном исчислении функция Гамильтона имеет вид , то есть совпадает с (4.13) с точностью до обозначений. Сравним уравнения:

- уравнение Беллмана,

- уравнение Гамильтона-Якоби.

Гамильтониан содержит управление , которое получалось бы из необходимого условия экстремума . Уравнение Беллмана является развитием результатов классического вариационного исчисления, распространяющим их на системы с ограничением на управление ( ).

30. Рассмотрим решение задачи минимизации, когда функционал содержит только терминальный член: , .

Пусть доказано существование функции Беллмана, удовлетворяющей уравнению (4.4):

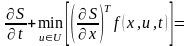
. (4.14)

Минимум скалярного произведения двух векторов достигается, если они направлены в противоположные стороны. Поскольку (фазовая скорость), то можно сделать вывод, что оптимальный вектор фазовой скорости направлен против градиента функции .

На рис. 4.2 для двумерной задачи показано семейство линий уровней функции и положение ее минимального значения, а также одна из траекторий движения, приводящая к минимуму.

Рис. 4.2. Семейство линий уровней функции S

В случае ограничений на управление , а значит, и на вектор фазовой скорости, , движение по антиградиенту может быть невозможно, тогда оптимальный вектор фазовой скорости выбирается из условия

.

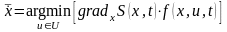31. Рассмотрим следующую задачу синтеза оптимального управления линейной динамической системой

, , , (4.16)

,

где матрицы , , , и в общем случае зависят от времени, причем и - положительно – определенные, матрица - постоянная.

Запишем уравнение Беллмана для системы (4.16)

(4.17)

с граничным условием

. (4.18)

Сначала будем решать задачу, сняв ограничения на управление. Тогда, осуществляя операцию минимизации в (4.17), получим

, . (4.19)

Тогда уравнение (4.17) принимает вид

. (4.20)

Решение этого уравнения будем искать в виде

, (4.21)

где - симметрическая матрица порядка ( ). Сравнивая (4.21) с (4.18), видим, что

. (4.22)

Подставляя (4.21) в (4.20), получим

(4.23)

Отсюда следует, что матрица должна удовлетворять уравнению

, (4.24)

которое может быть решено путем интегрирования от до с граничным условием (4.22). Это уравнение есть уже известное по предыдущей главе уравнение Риккати. Заметим, что проблемой при его решении может быть наличие «особых точек», то есть точек разрыва второго рода.

С учетом выражения (4.21) для функции будущих потерь получаем оптимальное управление в форме оптимального линейного регулятора

, (4.25)

где . (4.26)

Вернемся к первоначальной постановке задачи, учитывая ограничение на управление. Если , то проблемы не существует. В общем случае оптимальное управление состоит из двух режимов: (4.25) и граничного ( - граница множества ). Сложность заключается в том, что теперь для функции не существует единого выражения для всего пространства . При граничном управлении функция отличается от квадратичной формы и может быть найдена путем решения уравнения Беллмана с граничным управлением, например, методом характеристик, с последующей гладкой склейкой полученного решения и решения (4.21).

Рассмотренная выше задача называется задачей аналитического конструирования оптимальных регуляторов (задача АКОР).