
- •1. Задачи математического программирования называются также статическими задачами оптимизации.
- •2. Определение. Переменная величина называется функционалом от функции , если каждой функции из некоторого множества функций соответствует определенное значение .
- •4. Простейшей задачей вариационного исчисления называется задача об экстремуме функционала вида (2.1) с граничными условиями: , .
- •5. . Для того чтобы функционал
- •6. Изопериметрическими задачами, в узком смысле этого слова, называются задачи об отыскании геометрической фигуры максимальной площади при заданном периметре.
- •7. Исследуем на экстремум функционал, зависящий от функций,
- •8. 2.5. Основная формула для вариации функционала
- •12. Введем новые переменные и преобразуем основную формулу для вариации функционала (2.11):
- •15.Выражение для выражение для второй вариации принимает вид
- •18. Введение игольчатой вариации управления [1] позволило получить необходимое условие минимума функционала при ограничениях на управление.
- •19. Следующее дифференциальное уравнение для вектора – функции :
- •6. Окончательно задача оптимального управления приводится к краевой задаче для системы обыкновенных дифференциальных уравнений
- •24. . Задача программирования оптимального управления
- •2. Задача синтеза оптимального управления
- •25. Рассмотрим следующую задачу синтеза оптимального управления линейной динамической системой
- •27. Доказательство принципа максимума было проведено без учета ограничений на вектор состояния. Рассмотрим теперь следующую постановку задача. Дана автономная динамическая система
- •29. Запишем уравнение Беллмана (4.4)
- •30. Рассмотрим решение задачи минимизации, когда функционал содержит только терминальный член: , .
- •31. Рассмотрим следующую задачу синтеза оптимального управления линейной динамической системой
- •32. Рассмотрим задачу оптимального управления дискретной динамической системой
- •33. Рассмотрим линейную дискретную систему
- •34. При решении задачи синтеза оптимального управления нелинейной динамической системой
- •39. Пусть имеется функция , определенная на множестве . Требуется найти
- •40. Пусть задана динамическая система
4. Простейшей задачей вариационного исчисления называется задача об экстремуме функционала вида (2.1) с граничными условиями: , .
Лемма.
Если для каждой непрерывной функции
 выполняется условие обращения в нуль
интеграла
выполняется условие обращения в нуль
интеграла
 ,
,
где
функция
 непрерывна на отрезке
,
то
непрерывна на отрезке
,
то
 на том же отрезке.
на том же отрезке.
Доказательство.
Предположив, что в точке
 ,
лежащей на отрезке
,
лежащей на отрезке
 ,
,
 ,
придем к противоречию. Действительно,
из непрерывности функции
следует, что если
,
придем к противоречию. Действительно,
из непрерывности функции
следует, что если
 ,
то
сохраняет знак в некоторой окрестности
,
то
сохраняет знак в некоторой окрестности
 точки
точки
 ;
выбрав функцию
также сохраняющую знак в этой окрестности
и равную нулю вне этой окрестности,
получим
;
выбрав функцию
также сохраняющую знак в этой окрестности
и равную нулю вне этой окрестности,
получим
 ,
,
так
как произведение
 сохраняет знак на интервале
и обращается в нуль вне этого отрезка.
Итак, мы пришли к противоречию,
следовательно,
.
сохраняет знак на интервале
и обращается в нуль вне этого отрезка.
Итак, мы пришли к противоречию,
следовательно,
.
5. . Для того чтобы функционал
 ,
,
определенный на множестве непрерывных функций , имеющих непрерывную первую производную и удовлетворяющих граничным условиям , , достигал на экстремума, необходимо, чтобы функция удовлетворяла уравнению Эйлера
 ,
(2.5)
,
(2.5)
или в развернутом виде
 .
(2.6)
.
(2.6)
Доказательство.
Получим формулу для первой вариации
функционала. Применяя операцию
варьирования подынтегрального выражения
при условии, что
 ,
получим
,
получим
 .
(2.7)
.
(2.7)
Проинтегрируем
второе слагаемое по частям и, принимая
во внимание, что
 ,
получим
,
получим
 .
(2.8)
.
(2.8)
Но
поскольку концы экстремали закреплены,
то
 ,
,
 ,
и получаем необходимое условие экстремума
в виде
,
и получаем необходимое условие экстремума
в виде
 .
(2.9)
.
(2.9)
В
силу основной леммы вариационного
исчисления, поскольку
 ,
для любого
,
получаем результат (2.5).
,
для любого
,
получаем результат (2.5).
Интегральные
кривые уравнения Эйлера
 называются экстремалями. Только на
них достигается экстремум рассматриваемого
функционала. Чтобы установить, реализуется
ли на них в действительности экстремум,
и притом максимум или минимум, надо
воспользоваться достаточными условиями
экстремума.
называются экстремалями. Только на
них достигается экстремум рассматриваемого
функционала. Чтобы установить, реализуется
ли на них в действительности экстремум,
и притом максимум или минимум, надо
воспользоваться достаточными условиями
экстремума.
Краевая задача для уравнения (2.6) с граничными условиями , не всегда имеет решение, а если решение существует, то оно может быть не единственным.
Получим
необходимые условия экстремума
функционала
,
зависящего от
независимых функций
 :
:

при заданных граничных условиях всех функций
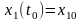 ,
,
 ,...,
,...,
 ,
,
 ,
,
 ,...,
,...,
 .
.
Если
варьировать одну из функций
 ,
оставляя остальные неизменными, то
рассматриваемый функционал превращается
в функционал, зависящий лишь от одной
функции, которая, следовательно, должна
удовлетворять уравнению Эйлера
,
оставляя остальные неизменными, то
рассматриваемый функционал превращается
в функционал, зависящий лишь от одной
функции, которая, следовательно, должна
удовлетворять уравнению Эйлера
 .
.
Так как это рассуждение применимо к любой функции , то мы получим систему дифференциальных уравнений второго порядка
 ,
(2.10)
,
(2.10)
определяющих
 -параметрическое
семейство интегральных кривых
(экстремалей).
-параметрическое
семейство интегральных кривых
(экстремалей).
6. Изопериметрическими задачами, в узком смысле этого слова, называются задачи об отыскании геометрической фигуры максимальной площади при заданном периметре.
В настоящее время изопериметрическими задачами называется значительно более широкий класс задач, а именно, все вариационные задачи, в которых требуется определить экстремум функционала
,
при наличии так называемых изопериметрических условий
 ,
,
где
 - постоянные
,
а
- постоянные
,
а
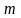 может быть меньше или равно
.
может быть меньше или равно
.
Рассмотрим следующую изопериметрическую задачу.
Среди
всех кривых
,
удовлетворяющих условиям
,
 ,
на которых функционал
,
на которых функционал
 ,
,
найти такую, которая дает экстремум функционалу
 .
.
Пусть
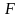 и
и
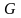 имеют непрерывные производные на отрезке
.
Если искомая кривая не является
экстремалью функционала
,
тогда имеет место теорема [1].
имеют непрерывные производные на отрезке
.
Если искомая кривая не является
экстремалью функционала
,
тогда имеет место теорема [1].
Теорема
2.3. Если кривая
обеспечивает экстремум функционала
и удовлетворяет условиям
 ,
,
,
но не является экстремалью функционала
,
то существует такое число
,
,
,
но не является экстремалью функционала
,
то существует такое число
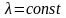 ,
что
является экстремалью функционала
,
что
является экстремалью функционала
 .
(2.15)
.
(2.15)
Этот
результат используется следующим
образом. Составляется уравнение Эйлера
для функционала
.
Получается дифференциальное уравнение
второго порядка и находится его общее
решение
 ,
которое содержит параметр
,
которое содержит параметр
 и две произвольные постоянные. Эти три
величины определяются из граничных
условий и условия
и две произвольные постоянные. Эти три
величины определяются из граничных
условий и условия
 .
.
