32. Рассмотрим задачу оптимального управления дискретной динамической системой

, , . (4.28)

Здесь - -мерный вектор состояния, - -мерный вектор управлений, - номер шага. Функционал в данной постановке имеет вид

. (4.29)

Полученную задачу отыскания оптимального управления на каждом из шагов можно решать методами нелинейного программирования, однако ее размерность может оказаться настолько большой, что практически ее решение не может быть получено. Воспользуемся принципом оптимальности Беллмана. Рассмотрим последний шаг управления при . В соответствии с принципом оптимальности не зависит от предыстории системы и определяется только состоянием . Затраты на перевод системы из состояния в равны

. (4.30)

Минимизируя эти затраты по , находим искомый закон управления. Обозначим функцию будущих потерь на последнем шаге :

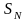. (4.31)

Полагая, что найдена, перейдем к предпоследнему шагу . Теперь будущее поведение системы полностью определяется состоянием 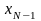и управлением и , которые должны быть выбраны из условия минимизации функционала

. (4.32)

Первое слагаемое не зависит от , поэтому введя обозначение , получим

(4.33)

.

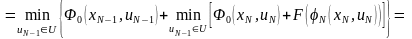
Аналогично, для произвольного шага можно получить основное рекуррентное соотношение метода динамического программирования

. (4.34)

равно минимальному значению критерия оптимальности, которое может быть получено при движении из состояния в конечное состояние и может быть выражено формулой

. (4.35)

Соотношение можно рассматривать как граничное условие для основного рекуррентного соотношения. Применяя основное рекуррентное соотношение последовательно, начиная с , можно найти оптимальный закон управления для всех шагов последовательно и вместе с тем зависимость функции будущих потерь от . При этом на каждом шаге минимизация осуществляется лишь по текущему вектору управления . Таким образом, метод динамического программирования приводит к алгоритму численного решения задачи синтеза оптимального управления путем последовательной минимизации функции многих переменных.

Основная трудность при решении задач с большой размерностью заключается в требовании большой памяти ЭВМ для запоминания на каждом шаге значений функции будущих потерь, зависящей от текущего состояния системы. Эту проблему принято называть «проклятием размерности».

33. Рассмотрим линейную дискретную систему

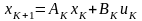, , (4.36)

где - -мерный вектор состояния, - -мерный вектор управлений ( - не ограничено), - номер шага. Функционал в данной постановке имеет вид

. (4.37)

Здесь , матрицы с размерами и соответственно, зависящие от номера шага ; , и - положительно-определенные матрицы.

Основное рекуррентное соотношение (4.34) принимает вид

, (4.38)

где 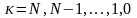, причем .

Полагая и учитывая граничное условие, получаем

. (4.39)

Оптимальное управление должно удовлетворять необходимому условию , откуда

.

Получаем

, (4.40)

где

, . (4.41)

Следовательно, оптимальное управление на последнем шаге линейно зависит от фазового вектора.

Предположим, что обратная матрица существует. Если матрицы и положительно определенные, то управление удовлетворяет и достаточному условию минимума.

Подставим найденное управление в выражение для :

(4.42)

или , где обозначена матрица

(4.43)

Перейдем к следующему шагу, полагая . Так как вид функций и одинаков, то после использования основного рекуррентного соотношения получим функцию в таком же виде. То есть, для любого функция может быть представлена в виде квадратичной формы . Таким образом, в рассматриваемом случае закон оптимального управления на каждом шаге является линейным. Матрицу называют матрицей коэффициентов обратной связи, так как она характеризует связь вектора управления с вектором фазовых координат .

Таким образом, получаем закон управления

, (4.44)

где

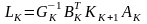, , (4.45)

, (4.46)

причем

. (4.47)

Соотношения (4.44) – (4.47) зададут синтез управления в форме оптимального линейного дискретного регулятора.