
- •1. Задачи математического программирования называются также статическими задачами оптимизации.
- •2. Определение. Переменная величина называется функционалом от функции , если каждой функции из некоторого множества функций соответствует определенное значение .
- •4. Простейшей задачей вариационного исчисления называется задача об экстремуме функционала вида (2.1) с граничными условиями: , .
- •5. . Для того чтобы функционал
- •6. Изопериметрическими задачами, в узком смысле этого слова, называются задачи об отыскании геометрической фигуры максимальной площади при заданном периметре.
- •7. Исследуем на экстремум функционал, зависящий от функций,
- •8. 2.5. Основная формула для вариации функционала
- •12. Введем новые переменные и преобразуем основную формулу для вариации функционала (2.11):
- •15.Выражение для выражение для второй вариации принимает вид
- •18. Введение игольчатой вариации управления [1] позволило получить необходимое условие минимума функционала при ограничениях на управление.
- •19. Следующее дифференциальное уравнение для вектора – функции :
- •6. Окончательно задача оптимального управления приводится к краевой задаче для системы обыкновенных дифференциальных уравнений
- •24. . Задача программирования оптимального управления
- •2. Задача синтеза оптимального управления
- •25. Рассмотрим следующую задачу синтеза оптимального управления линейной динамической системой
- •27. Доказательство принципа максимума было проведено без учета ограничений на вектор состояния. Рассмотрим теперь следующую постановку задача. Дана автономная динамическая система
- •29. Запишем уравнение Беллмана (4.4)
- •30. Рассмотрим решение задачи минимизации, когда функционал содержит только терминальный член: , .
- •31. Рассмотрим следующую задачу синтеза оптимального управления линейной динамической системой
- •32. Рассмотрим задачу оптимального управления дискретной динамической системой
- •33. Рассмотрим линейную дискретную систему
- •34. При решении задачи синтеза оптимального управления нелинейной динамической системой
- •39. Пусть имеется функция , определенная на множестве . Требуется найти
- •40. Пусть задана динамическая система
12. Введем новые переменные и преобразуем основную формулу для вариации функционала (2.11):
 ,
(2.21)
,
(2.21)
 .
(2.22)
.
(2.22)
Тогда

 .
(2.23)
.
(2.23)
Система уравнений Эйлера
 (2.24)
(2.24)
заменяется системой уравнений первого порядка канонического вида:
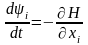 ,
,
 .
(2.25)
.
(2.25)
Функция
 называется функцией Гамильтона, а
переменные
называется функцией Гамильтона, а
переменные
 - сопряженными переменными. Дифференциальные
уравнения для сопряженных переменных
(2.25) называются сопряженной системой
уравнений.
- сопряженными переменными. Дифференциальные
уравнения для сопряженных переменных
(2.25) называются сопряженной системой
уравнений.
Если функция не зависит явно от , то функция является первым интегралом уравнений Эйлера. Действительно,
 .
(2.26)
.
(2.26)
Используя
каноническую форму уравнений Эйлера,
получим при

 ,
(2.27)
,
(2.27)
откуда
следует, что
 .
.
Рассмотрим
некоторую функцию
 .
.

 .
(2.28)
.
(2.28)
Выражение называется скобкой Пуассона. Таким
образом, чтобы функция
называется скобкой Пуассона. Таким
образом, чтобы функция
 ,
не зависящая явно от
,
была первым интегралом уравнений Эйлера
(
,
не зависящая явно от
,
была первым интегралом уравнений Эйлера
( ),
необходимо и достаточно, чтобы
),
необходимо и достаточно, чтобы
 .
.
13. Рассмотрим центральное поле экстремалей с центром в точке для функционала
 ,
.
,
.
На
экстремалях поля функционал
 превращается в функцию
превращается в функцию
 координат второй граничной точки
координат второй граничной точки
 .
Воспользуемся выражением для вариации
функционала (2.11)
.
Воспользуемся выражением для вариации
функционала (2.11)

 .
(2.29)
.
(2.29)
С
другой стороны
 .
.
Для
точки
:
 ,
,
 ,
тогда
,
тогда
 ,
,
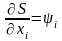 .
(2.30)
.
(2.30)
Следовательно,
 .
(2.31)
.
(2.31)
Это уравнение (2.32) называется уравнением Гамильтона-Якоби.
В
этом случае решение канонической системы
равносильно решению дифференциального
уравнения в частных производных
относительно неизвестной функции

 (2.32)
(2.32)
с
граничным условием
 .
.
14. Для нахождения необходимого условия слабого минимума функционала введем понятие второй вариации функционала. Функционал имеет вторую вариацию, если его приращение можно представить в виде
 ,
(2.33)
,
(2.33)
где
 - линейный относительно вариации функции
функционал (первая вариация функционала);
- линейный относительно вариации функции
функционал (первая вариация функционала);
 - квадратичный относительно
функционал вторая
вариация функционала;
- квадратичный относительно
функционал вторая
вариация функционала;
 - содержит члены высших порядков малости
(
- содержит члены высших порядков малости
( при
),
Пусть
при
),
Пусть
 .
.
Теорема 2.5. Для того чтобы функционал достигал своего минимума на кривой , необходимо чтобы выполнялись условия
,
 .
(2.34)
.
(2.34)
Доказательство.
Пусть имеется кривая
,
которая неограниченно приближается к
экстремали
.
Это означает, что
 ,
т.е. кривые сближаются. Тогда
,
т.е. кривые сближаются. Тогда
 ,
,
 ,
следовательно, знак
определяется знаком
,
следовательно, знак
определяется знаком
 .
Это означает, что неотрицательность
второй вариации обеспечивает слабый
минимум функционала.
.
Это означает, что неотрицательность
второй вариации обеспечивает слабый
минимум функционала.
Получим формулу для второй вариации функционала в задаче с закрепленными концами. Зададим функционал
с
граничными условиями
 .
В этом случае первая и вторая вариации
функционала определяются формулами
.
В этом случае первая и вторая вариации
функционала определяются формулами
 ,
,
 .
(2.35)
.
(2.35)
Интегрируя по частям среднее слагаемое в подынтегральном выражении формулы (2.35), получим
 .
.
Тогда,
с учетом
 ,
,
 ,
получим
,
получим
 .
(2.36)
.
(2.36)
Получим
условие, при котором
.
Введем произвольную непрерывную и
дифференцируемую функцию
 такую, что, будучи введенной в интегральное
выражение (2.36), она с точностью до
множителя преобразует его в точный
квадрат. Показано [2], что если
дифференциальное уравнение
такую, что, будучи введенной в интегральное
выражение (2.36), она с точностью до
множителя преобразует его в точный
квадрат. Показано [2], что если
дифференциальное уравнение
 (2.37)
(2.37)
имеет на отрезке
 дифференцируемое решение
,
то
дифференцируемое решение
,
то
