6. Окончательно задача оптимального управления приводится к краевой задаче для системы обыкновенных дифференциальных уравнений
,
,
(3.41)
с начальными условиями
,
.
(3.42)
Здесь
- неизвестные начальные условия для
компонентов вектор-функции
,
подлежащие определению в ходе решения
краевой задачи, которая заключается в
подборе
параметров
,
так, чтобы при
выполнялось
условий (граничных – для вектора
или условий трансверсальности для
).
Зададим эти условия в общем виде
,
.
(3.43)
Схема
решения краевой задачи такова. Зададим
начальное приближение
и проинтегрируем каноническую систему
до момента
:
,
,
(3.44)
Затем,
вычисляя функции
,
строим итерационную схему (см. гл. 7)
,
на каждом шаге которой принимается
решение либо о продолжении вычислений,
либо об их прекращении в случае, когда
,
(3.45)
где - заданный уровень погрешности.
23. Задачи оптимизации, в которых производится минимизация времени перехода из начального состояния в конечное, называются задачами об оптимальном (максимальном) быстродействии. Рассмотрим случай линейной системы с постоянными коэффициентами:
.
(3.46)
Здесь
- вектор состояния
,
- вектор управления
,
и
- постоянные матрицы порядков
и
.
Будем полагать, что компоненты вектора
управления ограничены по величине:
:
,
.
Множество
представляет собой гиперпараллелепипед
в
-мерном
пространстве с гранями, равными
.
В задачах об оптимальном быстродействии критерий оптимальности имеет вид
.
Для выявления структуры оптимального управления воспользуемся необходимыми условиями в задаче Лагранжа. Составим Гамильтониан
,
(3.47)
где
,
.
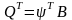Каноническая система уравнений принимает вид
, 
,
,
.
(3.48)
Оптимальное
управление
определяется из условия максимизации
гамильтониана:
,
если
,
,
если
,
,
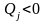или в векторной форме:
.
(3.49)
Если
на некотором отрезке времени
,
то задача называется вырожденной, а
управление может быть любым, поскольку
гамильтониан от него не зависит. Однако
в данной постановке случай вырожденности
не имеет места.
Так
как
свободно,
или
для любого
.
Отсюда следует, что
- ненулевой вектор для всех
,
задача невырождена.
Полученный
результат приводит к следующей теореме
(А.А.Фельдбаум). Если задача невырождена,
а все корни характеристической системы,
соответствующей рассматриваемой
математической модели (3.46), являются
действительными числами, то оптимальное
управление имеет не более
переключений. В случае комплексных
корней число переключений также конечно,
но зависит от начального и конечного
состояний системы
и
.
Отметим,
что уравнение
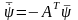может быть решено независимо от уравнения,
описывающего динамику системы, в виде
,
где
.
Предположим, что алгоритм решения
канонической системы (3.48) существует.
Тогда для каждого момента времени
могут быть найдены векторы
,
и установлена (в общем случае численно)
зависимость
.
Фактически получается решение задачи
синтеза оптимального управления:
,
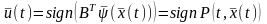(3.50)
где
функция
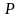называется функцией переключения.