18. Введение игольчатой вариации управления [1] позволило получить необходимое условие минимума функционала при ограничениях на управление.

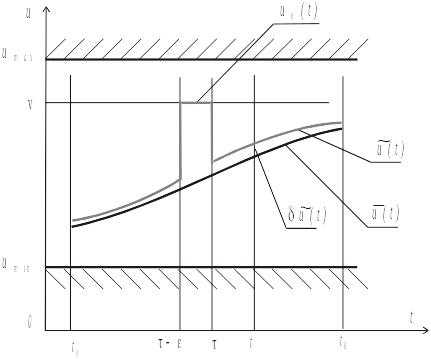
Рис. 3.1. Вариации управления

Обычно вариация управления рассматривается как гладкая функция . Игольчатой вариацией называется разность (рис. 3.1), где при , при , - некоторое значение управления, достаточно сильно отличающееся от , при этом , - бесконечно малая положительная величина.

Влияние игольчатого варьирования управления на поведение системы аналогично влиянию короткого импульса (рис. 3.2).

Рис. 3.2. Влияние игольчатого варьирования управления на поведение системы

Степень влияния импульса определяется площадью . Поскольку эта величина при становится бесконечно малой, то ее влияние на дальнейшее движение системы бесконечно мало. Малость возмущения управления позволяет использовать линеаризованную модель возмущенного движения, что упрощает решение задачи, а также рассматривать вариации управления в разные моменты времени независимо друг от друга.

19. Следующее дифференциальное уравнение для вектора – функции :

. (3.13)

Это уравнение может быть решено лишь совместно с исходной системой, т.к. в него входят и .

, , . (3.18)

Условие (3.18) называется еще условиями трансверсальности. Соотношения (3.13) - (3.18) задают необходимые условия оптимальности, получившие название «Принцип максимума Понтрягина». Сформулируем их в виде основной теоремы [1].

Если и суть оптимальная траектория и оптимальное управление, обеспечивающие минимум функционалу , с заданными граничными условиями и ограничениями на управление, то существует ненулевая и непрерывная вектор-функция , удовлетворяющая канонической системе дифференциальных уравнений и условиям трансверсальности, такая, что функция Гамильтона для любого момента времени достигает своего максимума на множестве при управлении .

20. На оптимальной траектории гамильтониан обладает следующими свойствами.

1. Гамильтониан - непрерывная функция времени для всех .

Это свойство очевидно для любого , не совпадающего с точками разрыва управления . Пусть - одна из точек разрыва. Рассмотрим значения слева и справа от точки . В силу непрерывности по времени и можно записать

,

.

Предположим, что . Возможны два случая: и .

Однако и то, и другое противоречат основной теореме принципа максимума, согласно которой гамильтониан всегда принимает максимальное значение. Следовательно, , то есть функция H непрерывна.

2. Гамильтониан постоянен на оптимальной траектории, т.е. для всех .

Рассмотрим некоторый отрезок , на котором функция непрерывна. Для любых близких в силу основной теоремы принципа максимума

(3.19)

и поэтому

.

Если , то

.

При получаем неравенство

. (3.20)

Но правая часть равна нулю, что следует из канонической системы уравнений. Следовательно,

. (3.21)

Если , то аналогично получаем, что

. (3.22)

Из (3.21) и (3.22) следует, что , т.е. для всех . В силу непрерывности по времени для всех .

3. Если свободно, то для всех .

Проварьируем управление в конечный момент времени , изменив величину на бесконечно малую величину и сохранив при этом значение величину . В отличие от игольчатой такая вариация называется временной вариацией управления. Вариация траектории 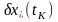с точностью до малых высшего порядка будет равна

. (3.23)

Умножив на с учетом (3.9), получим

.

Так как может быть положительным и отрицательным, то

.

Поскольку Гамильтониан на всей оптимальной траектории постоянен, поэтому

для всех .

21. Для отыскания оптимального управления с помощью полученных необходимых условий требуется решить каноническую систему из уравнений (3.17). Поэтому должно быть задано граничных условий. Если начальный вектор задан, то в начальный момент времени имеется условий. Недостающие условий определяются типом граничных условий исходной задачи в соответствии с условиями трансверсальности.

1. Задача с фиксированным концом траектории

Если задан, то совместно с имеем условий, которые замыкают каноническую систему уравнений, образуя краевую задачу. Граничное условие

(3.24)

выполняется автоматически, так как .

2. Задача со свободным концом траектории

Если свободен, то для выполнения (3.24) необходимо . Снова получаем краевую задачу, отличающуюся от предыдущей тем, что в момент вместо вектора задан : ( , ).

3. Задача попадания на заданную терминальную поверхность

Предполагается, что вектор должен принадлежать некоторой поверхности , где - вектор размерности . Это означает, что вариация должна удовлетворять соотношению

. (3.25)

Сравнивая это выражение с (3.24), заключаем, что для их одновременного выполнения необходимо существование такого постоянного вектора размерности , чтобы

. (3.26)

Приходим к краевой задаче, в которой заданными являются векторы и с точностью до вектора . Для определения необходимо к канонической системе уравнений добавить уравнение поверхности , которое дает дополнительно условий.

4. Задача выбора начальной точки движения

Можно показать, что, если неизвестно, то к граничному условию (3.24) необходимо добавить аналогичное условие для момента : .

22. Алгоритмом решения задачи оптимального управления будем называть последовательность действий, позволяющих привести задачу к стандартной процедуре отыскания аналитического или численного решения. На основе результатов п. 3.3 – 3.5 этот алгоритм можно представить в следующем виде.

1. Дается математическая формулировка задачи в форме Майера, Лагранжа или Больца: записываются уравнения динамической системы, функционал, граничные условия и ограничения на управление.

2. составляется функция Гамильтона:

. (3.27)

Здесь вектор-функция правых частей динамической системы, компонента в соответствии с (3.24) принята равной -1.

4. записываем уравнения сопряженной системы

,

, (3.30)

где .

В итоге каноническая система принимает вид

, , . (3.31)

5. Исследуются граничные условия и соответствующие им условия трансверсальности (п. 3.5). Окончательно формируется сводка необходимых условий оптимальности:

а) Задача Майера:

, , , , .

Необходимые условия оптимальности управления имеют вид.

, ,

, , ,

где .

для всех .

, если фиксировано,

для всех , если свободно.

б) Задача Лагранжа:

, , , ,

.

Компоненты и исключены, поскольку в этом случае функции и от них не зависят.

Необходимые условия оптимальности управления имеют вид.

, ,

, ,

где .

для всех .

, если фиксировано,

для всех , если свободно.

в) Задача управления конечным состоянием (задача Больца):

, , , , (3.32)

.

Функция характеризует конечное состояние системы в момент . Естественно, что 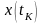считается нефиксированным. Рассматриваемая задача может быть сведена к задаче Лагранжа. Действительно, функционал можно представить в виде

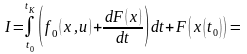
. (3.33)

Здесь при фиксированных начальных условиях есть некоторая константа, которую можно не учитывать. Необходимые условия оптимальности имеют вид:

, , , , (3.34)

где .

для всех .

Здесь - сопряженная вектор-функция в задаче Больца. , если фиксировано, для всех , если свободно.

Вводя вектор функцию

(3.35)

и гамильтониан

, (3.36)

приходим к соотношениям

,

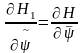, . (3.37)

С учетом этого заключаем, что необходимые условия оптимальности в задаче Больца отличаются от соответствующих условий в задаче Лагранжа лишь граничным условием

. (3.38)

Замечание. Случай неавтономной системы. Если исходная динамическая система оказывается неавтономной, то путем введения дополнительной переменной ее можно формально свести к автономной и тем самым использовать уже полученные необходимые условия. Отличием от прежних условий является то, что гамильтониан теперь явно зависит от времени и не может считаться постоянным при . С учетом запишем

. (3.39)

Здесь аддитивная переменная не влияет на результат оптимизации гамильтониана, т.к.

. (3.40)