18. Коррелированность и зависимость случайных величин. Нормальный закон распределения на плоскости

Две случайные величины X и У называют коррелированными, если их корреляционный момент (или, что то же, коэффициент корреляции) отличен от нуля; X и У называют некоррелированными величинами, если их корреляционный момент равен нулю.

Две коррелированные величины также и зависимы. Действительно, допустив противное, мы должны заключить, что µxy =0, а это противоречит условию, так какдля коррелированных величин µxy ≠ 0.

Обратное предположение не всегда имеет место, т. е. если две величины зависимы, то они могут быть как коррелированными, так и некоррелированными. Другими словами, корреляционный момент двух зависимых величин может быть не равен нулю, но может и равняться нулю.

Из коррелнрованности двух случайных величин следует их зависимость, но из зависимости еще не вытекает коррелированность. Из независимости двух величин следует их некоррелированность, но из некоррелированности еще нельзя заключить о независимости этих величин.

На практике часто встречаются двумерные случайные величины, распределение которых нормально.  Нормальным законом распределения на плоскостиназывают распределение вероятностей двумерной случайной величины (X, Y), если

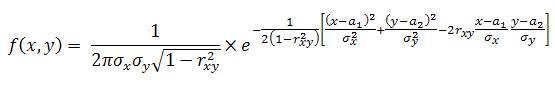
Мы видим, что нормальный закон на плоскости определяется пятью параметрами: а₁, а₂, σ_х, σ_у и r_xу. Можно доказать, что эти параметры имеют следующий вероятностный смысл: а₁, а₂ — математические ожидания,σ_х, σ_у — средние квадратические отклонения, r_xу — коэффициент корреляции величин X и У.  Убедимся в том, что если составляющие двумерной нормально распределенной случайной величины некоррелированны, то они и независимы. Действительно, пусть X и Y некоррелированны. Тогда, полагая в формулеr_xу = 0, получим

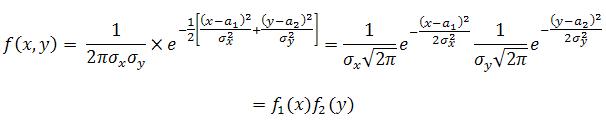
Таким образом, если составляющие нормально распределенной случайной величины некоррелированны, то плотность совместного распределения системы равна произведению плотностей распределения составляющих, а отсюда и следует независимость составляющих. Справедливо и обратное утверждение. Итак, для нормально распределенных составляющих двумерной случайной величины понятия независимости и некоррелированности равносильны.

19. Линейная регрессия. Прямые линии среднеквадратической регрессии. Линейная корреляция. Нормальная корреляция.

Рассмотрим двумерную случайную величину (X, Y), где X и У—зависимые случайные величины. Представим одну из величин как функцию другой. Ограничимся приближенным представлением (точное приближение, вообще говоря, невозможно) величины Y в виде линейной функции величины X:

где α и β — параметры, подлежащие определению. Это можно сделать различными способами: наиболее употребительный из них—метод наименьших квадратов.

Функцию g(X)=αX+β называют «наилучшим приближением» Y в смысле метода наименьших квадратов, если математическое ожидание М [Y—g(X)]2 принимает наименьшее возможное значение; функцию g(x) называют среднеквадратической регрессией Y на X.

Теорема. Линейная средняя квадратическая регрессия Y на X имеет вид

где m_x=M(X), m_y=M(Y), σ_x=√D(X),  σ_y=√D(Y),  r=µ_xy/(σ_xσ_y)—коэффициент корреляции величин X и Y.

Коэффициент β=rσ_y/σ_x называют коэффициентом регрессии Y на X, а прямую

называют прямой среднеквадратической регрессии Y на X. Подставив найденные значения α и β в соотношение (*), получим минимальное значение функции F (α, β), равное σ_y²(1—r²). Величину σ_y²(1—r²) называют остаточной дисперсией случайной величины Y относительно случайной величины X; она характеризует величину ошибки, которую допускают при замене У линейной функцией g(X)=α + βX. При r = ±1 остаточная дисперсия равна нулю; другими словами, при этих крайних значениях коэффициента корреляции не возникает ошибки при представлении Y в виде линейной функции от X.  Итак, если коэффициент корреляции г = ± 1, то Y и X связаны линейной функциональной зависимостью.  Аналогично можно получить прямую среднеквадратической регрессии X на Y:

(rσ_x/σ_y — коэффициент регрессии X на Y) и остаточную дисперсию σ_x²(1—r²) величины X относительно Y.  Если r = ± 1, то обе прямые регрессии, как видно из уравнений, совпадают.  Из уравнений прямых среднеквадратической регрессии следует, что обе прямые регрессии проходят через точку (m_x; m_y), которую называют центром совместного распределения величин X и Y.

Рассмотрим двумерную случайную величину (X, Y). Если обе функции регрессии У на X и X на У линейны, то говорят, что X и Y связаны линейной корреляционной зависимостью. Очевидно, что графики линейных функций регрессии — прямые линии, причем можно доказать, что они совпадают с прямыми среднеквадратической регрессии. Имеет место следующая важная теорема.  Теорема. Если двумерная случайная величина (X, Y) распределена нормально, то X и Y связаны линейной корреляционной зависимостью.  Доказательство. Двумерная плотность вероятности

,

где u = (х—а₁)/σ_x, v = (y—a₂)/σ_y. (**)

Плотность вероятности составляющей X

Найдем функцию регрессии М (Y | х), для чего сначала найдем условный закон распределения величины Y при Х=х

Подставив (*) и (***) в правую часть этой формулы и выполнив выкладки, имеем

Заменив u и v по формулам (**), окончательно получим

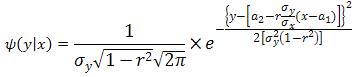
Полученное условное распределение нормально с математическим ожиданием (функцией регрессии У на X)

M(Y|x)=a₂+(x-a₁)rσ_y/σ_x

и дисперсией σ_y²(1—r²).  Аналогично можно получить функцию регрессии X на Y:

M(X|y)=a₁+(y—a₂)rσ_x/σ_y

Так как обе функции регрессии линейны, то корреляция между величинами X и Y линейная, что и требовалось доказать.  Принимая во внимание вероятностный смысл параметров двумерного нормального распределения, заключаем, что уравнения прямых регрессии

y—a₂= (x—a₁)rσ_y/σ_x, x—a₁= (y—a₂)rσ_x/σ_y

совпадают с уравнениями прямых среднеквадратической регрессии