21. Основные понятия математической статистики. Числовые характеристика вариативного ряда

Математическая статистика – это наука, изучающая случайные явления посредством обработки и анализа результатов наблюдений и измерений.

Первая задача математической статистики – указать способы получения, группировки и обработки статистических данных, собранных в результате наблюдений, специально поставленных опытов или произведённых измерений.

Вторая задача математической статистики – разработка методов анализа статистических сведений в зависимости от целей исследования. Например, целью исследования может быть:

- оценка неизвестной вероятности события;

- оценка параметров распределения случайной величины;

- оценка неизвестной функции распределения случайной величины;

- проверка гипотез о параметрах распределения или о виде неизвестного распределения;

- оценка зависимости случайной величины от одной или нескольких случайных величин и т.д.

Случайную величину будем называть генеральной совокупностью .

Исходным материалом для изучения свойств генеральной совокупности являются статистические данные, т.е. значения , полученные в результате повторения случайного опыта (измерения случайной величины ). Предполагается, что опыт может быть повторён сколько угодно раз в неизменных условиях. Это означает, что распределение случайной величины , , заданной на множестве исходов -го опыта, не зависит от и совпадает с распределением генеральной совокупности .

Набор независимых в совокупности случайных величин , где соответствует -му опыту, называют случайной выборкой из генеральной совокупности . Число называется объёмом выборки.

Совокупность чисел , полученных в результате -кратного повторения опыта по измерению генеральной совокупности , называется реализацией случайной выборки или просто выборкой объёма .

В основе большинства результатов математической статистики лежит выборочный метод, состоящий в том, что свойства генеральной совокупности устанавливаются путём изучения тех же свойств на случайной выборке.

N-объем генеральных совокупностей

n- объем выборки, кол-во которых были подвергнуты иследованию

Выборка представляет совокупность n чисел

Наблюдаемое значение признака наз-ся вариантами обозначим через Хi из чисел найти самое большое и самое маленькое x min и x max

Совокупность чисел (x1,x2….xn), полученных в результате n -кратного повторения опыта по измерению генеральной совокупности x, называется реализацией случайной выборки или просто выборкой объёма n.

В основе большинства результатов математической статистики лежит выборочный метод, состоящий в том, что свойства генеральной совокупности x устанавливаются путём изучения тех же свойств на случайной выборке.

1.Если n не велико то выборку просто ранжируют в порядке возр и убывания

2.Если среди вариантов имеются повтряющиеся то строят дискрет вариационный ряд

Выборка бывает повторная и бесповторная

Повторной называют при которрой отборный эффект возвращается в генеральную совокупность

Бесповторной называют при которой отборный объект в ген совокуп не возвращается. На практике используют чаще всего бесповторную

Интервальные оценки параметров распределения.

  Интервальной называют оценку, которая определяется двумя числами—концами интервала. Интервальные оценки позволяют установить точность и надежность оценок .

Пусть найденная по данным выборки статистическая характеристика Q* служит оценкой неизвестного пара­метра Q. Будем считать Q постоянным числом (Q может быть и случайной величиной). Ясно, что Q* тем точнее определяет параметр Q, чем меньше абсолютная величина разности |Q- Q*|. Другими словами, если d>0 и |Q- Q*| <d , то чем меньше d , тем оценка точнее.

  Таким образом, положительное число d характеризует точность оценки.

Однако статистические методы не позволяют категорически утверждать, что оценка Q* удовлетворяет неравенству |Q- Q*| <d; можно лишь говорить о вероятности g, с которой это неравенство осуществляется.

  Надежностью (доверительной вероятностью) оценки называют вероятность g , с которой осуществляется неравенство |Q—Q* | <d .

Обычно надежность оценки задается наперед, причем в качестве g берут число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999.

Пусть вероятность того, что, |Q- Q*| <d равна g:

P(|Q- Q*| <d)= g.

Заменив неравенство равносильным ему двойным неравенством получим:

Р [Q* —d< Q < Q* +d] = g

Это соотношение следует понимать так: вероятность того, что интервал Q* - d< Q < Q* +d заключает в себе (покрывает) неизвестный параметр Q, равна g.

Интервал (Q* - d Q* +d) называется доверительным интервалом , который покрывает неизвестный параметр с надежностью g.

Интервальные оценки параметров нормального распределения.

Доверительный интервал для оценки математического ожидания при известном s.

Пусть количественный признак генеральной совокупности распределен нормально. Известно среднее квадратическое отклонение этого распределения -s. Требуется оценить математическое ожидание а по выборочной средней. Найдем доверительный интервал, покрывающий а с надежностью g. Выборочную среднюю будем рассматривать как случайную величину ( она изменяется от выборки к выборке), выборочные значения признака- как одинаково распределенные независимые СВ с математическим ожиданием каждой а и средним квадратическим отклонением s. Примем без доказательства, что если величина Х распределена нормально, то и выборочная средняя тоже распределена нормально с параметрами

.

Потребуем, чтобы выполнялось равенство

Заменив Х и s, получим

 

получим

Задача решена. Число t находят по таблице функции Лапласа Ф(х).

Доверительный интервал для оценки математического ожидания при неизвестном s.

Т.к. мы не знакомы с законами распределения СВ, которые используются при выводе формулы, то примем ее без доказательства.

В качестве неизвестного параметра s используют исправленную дисперсию s² . Заменяя s на s, t на величину t_g. Значение этой величины зависит от надежности g и объема выборки n и определяется по " Таблице значений t_g."  Итак :

и доверительный интервал имеет вид

Доверительный интервал для оценки дисперсии и среднего квадратического отклонения.

Требуется оценить неизвестную генеральную дисперсию и генеральное среднее квадратическое отклонение по исправленной дисперсии, т.е. найти доверительные интервалы, покрывающие параметры D и s с заданной надежностью g.

Потребуем выполнения соотношения

.

Раскроем модуль и получим двойное неравенство:

.

Преобразуем:

.

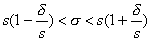Обозначим /ds q = (величина q находится по  "Таблице значений q"и зависит от надежности и объема выборки), д адготоверительный интервал для оценки генерального среднего квадратического отклонения имеет вид:

.

Замечание : Так как s >0, то если q >1 , левая граница интервала равна 0:

0< s < s ( 1 + q ).

Интервальная оценка вероятности биноминального распределения по относительной частоте.

Найдем доверительный интервал для оценки вероятности по относительной частоте, используя формулу:

 

Если n достаточно велико и р не очень близка к нулю и единице, то можно считать, что относительная частота распределена приближенно по нормальному закону, причем М(W)= р. Заменив Х на относительную частоту , математическое ожидание - на вероятность, получим равенство:

Приступим к построению доверительного интервала (р₁, р₂), который с надежностью g покрывает оцениваемый параметр р Потребуем, чтобы с надежностью g выполнялось соотношение указанное выше равенство:

                                                          Заменив

,

                                    получим:

Таким образом, с надежностью g выполняется неравенство (чтобы получить рабочую формулу, случайную величину W заменим неслучайной наблюдаемой относительной частотой w и подставим 1- р вместо q):

Учитывая, что вероятность р неизвестна, решим это неравенство относительно р. Допустим, что w > р. Тогда

 

Обе части неравенства положительны; возведя их в квадрат, получим равносильное квадратное неравенство относительно р:

Дискриминант трехчлена положительный, поэтому корни действительные и различные:

меньший корень

больший корень:

 

 Замечание1: При больших значениях n , пренебрегая слагаемыми

,и

                                                                     учитывая

получим приближенные формулы для границ доверительного интервала :

22. Статистическая гипотеза. Нулевая и конкурирующая, простая и сложная гипотезы. Ошибки первого и второго рода

Простой называют гипотезу, содержащую только одно предположение.

Сложной называют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез.

23. Статистический критерий проверки нулевой гипотезы. Наблюдаемое значение критерия. Критическая область. Область принятия гипотеза. Критические точки

личину обозначим через К.

24. Отыскание правосторонней, левосторонней и двусторонней критических областей

25. Сравнение двух дисперсий нормальных генеральных совокупностей.

26. Сравнение исправленной выборочной дисперсии с гипотетической генеральной дисперсией нормальной совокупности

27. Сравнение двух средних нормальных генеральных совокупностей, дисперсии которых известны