8. Функция распределения и её свойства

Среди событий х€В выделяют событие Х<x и вероятность случайной величины Х сопоставляется функция F(Х), определенная на всей числовой оси. Эта функция называется функцией распределения вероятностей случайной величины, т.еF(Х)=Р(Х<x). Геометрически это равенство можно истолковать так: F(Х) –это вероятность того, что случ величина примет значение, которое изображается на числ оси точкой, лежащей левее т. х.

Свойства:

• F(x) имеет значения [0;1];(вероятность-всегда неотр число)

• P(x₁<x<x₂)=F(x₂)-F(x₁) ()

• F(x) не убывает, т.е. если x1<x2, то F(x1)< F(x2);

• , ;

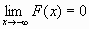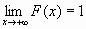• F(x) непрерывна справа, т.е.

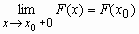
• Скачок в функции распределения в произвольную точку Х совпадает с вероятностью события x-X

9. Непрерывные случайные величины. Плотность вероятности и её свойства. Числовые характеристики непрерывной случайной величины

Случайная величина х называется непрерывной, если её функция распределения F(x) непрерывна при всех значениях х

Свойства:

1. Если х-непрерывная случайная величина, то P(x-x)=0

2. Вероятность попадания непрерывной случайной величины в интервалp(x₁<x<x₂)= p(x₁≤x<x₂)= p(x₁<x≤x₂)= p(x₁≤x≤x₂)

3. Если вычислить вероятность попадания непрерывной случайной величины в участок x₁≤x<x+∆х, то

P(x₁≤x<x+∆х)=F(x+∆х)-F(x) – приращение функции распределения на участке

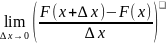= F’(x)=p(x)

Функция p(x)=F’(x) называется плотностью вероятности или плотностью распределения

Свойства:

1. p(x)≥0(т.к. функция распределения – неубывающая функция, значит и её производная – функция неотрицательная)

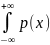2. =1(несобственный интеграл выражает вероятность события, состоящего в том, что случ величина примет значение, принадл интервалу(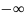 ; 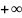). Очевидно, такое событие достоверно и его вероятн = 1

Числовые характеристики: см вопрос 7

10. Распределения дискретной случайной величины

По схеме Бернулли. Условия: проводимые испытания независимы, в каждом испытании возможны 2 исхода, вероятность появления события в каждом исходе постоянна. Тогда вероятность того, что в предлагаемых n испытаниях событие появится m раз распределяется по формуле :

Р_n(m)=C_n^m_*p­^m_*(1-p)^n-m– биномиальное распределение

P(m₁≤ m≤ m₂)=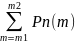

Наивероятнейшее значение m₀числа наступления события А при проведении nиспытаний при условии выполнения схемы Бернулли:

np-q≤m₀≤np+p

для приближенного вычисления вероятности используются след формулы:

1. Локальная формула Лапласа

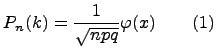
Где n - число опытов (испытаний),p - вероятность успеха,q=1-p - вероятность неуспеха,

,

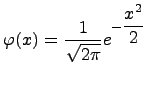
Функция четная :ɤ(-x)=ɤ(x)

Условия применения формулы: npq≥10

2. Формула Пуассона:

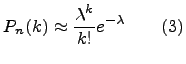
n - число опытов (испытаний),p - вероятность успеха,

Условия применения формулы: npq≤10

3. Интегральная формула Лапласа

Гдеn - число опытов (испытаний),p - вероятность успеха,q=1-p - вероятность неуспеха,

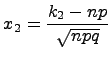
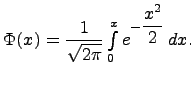
Функция четная: Ф(-х)=-Ф(х)

4. Геометрическое распределение

Дискретная случайная величина Х имеет геометрическое распределение, если ее возможные значения 0, 1, 2, ... , m, … , а вероятности этих значений: где 0 < p < 1, q = 1 – p ; m = 0, 1, 2, ... .

5. Гипергеометрическое распределение

Дискретная случайная величина Х имеет гипергеометрическое распределение если

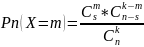
Где n – общее число испытаний, х-принимает значение из некоторого множества М, s-количество элементов, обладающих определенными свойствами, k- число выборки, m-число элементов, обладающих этим свойством и попавших в выборку.