1. Скалярное произведение векторов. Его основные свойства.

Определение скалярного произведения

Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла междуними.

Обозначается ab,а* b(или( а, b)).Итак, по определению,

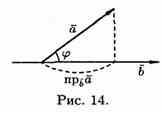
Формуле (6.1) можно придать иной вид. Так как | a| cosg=пр ba, (см. рис.14), a |b| cosg = пр ab, то получаем:

т. е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.

Свойства скалярного произведения

2. Скалярное произведение обладает переместительным свойством: ab=ba

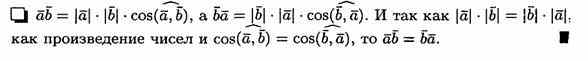
5. Если векторы а и b (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если a ^b, то ab=0. Справедливо и обратное утверждение: если ab=0 и а¹ 0 ¹b, то а ^ b

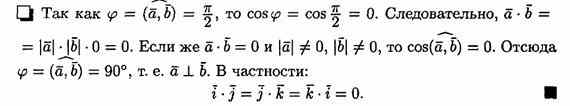
3. . Выражение скалярного произведения в координатах

Пусть заданы два вектора

Найдем скалярное произведение векторов, перемножая их как многочлены (что законно в силу свойств линейности скалярного произведения) и пользуясь таблицей скалярного произведения векторов i, j, k:

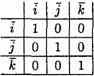
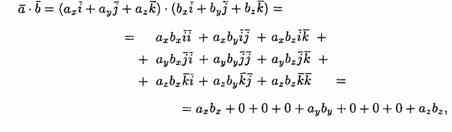
Т.е.

Итак, скалярное произведение векторов равно сумме произведений их одноименных координат.

Пример 6.2.

Доказать, что диагонали четырехугольника, заданного координатами вершин А(-4;-4;4), В(-3;2;2),C(2; 5;1), D(3;-2;2), взаимно перпендикулярны.

Решение: Составим вектора АС и BD, лежащие на диагоналях данного четырехугольника. Имеем: АС = (6;9;-3) и BD = (6;-4;0). Найдем скалярное произведение этих векторов:

АС • BD = 36 - 36 - 0 = 0.

Отсюда следует, что AC^BD. Диагонали четырехугольника ABCD взаимно перпендикулярны.

6.4. Некоторые приложения скалярного произведения

Угол между векторами

Определение угла φ между ненулевыми векторами а = (ax; ay; az) и b=( bх; bу; bг):

Отсюда следует условие перпендикулярности ненулевых векторов а и b:

Проекция вектора на заданное направление

Нахождение проекции вектора а на направление, заданное вектором b, может осуществляться по формуле

4. векторное произведение векторов. свойства.

Векторным произведением векторов a и b называется вектор c , который определяется следующими условиями:

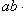
1. Его модуль равен 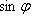где 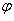- угол между векторами a и b

2. Вектор c перпендикулярен к плоскости, определяемой перемножаемыми векторами a и b.

3. Вектор c направлен так, что наблюдателю, смотрящему с его конца на перемножаемые векторы a и b, кажется, что для кратчайшего совмещения первого сомножителя со вторым первый сомножитель нужно вращать против часовой стрелки (см. рисунок).

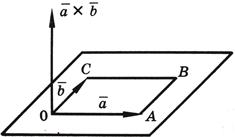
Векторное произведение векторов a и b обозначается символом

(25)

Или

(26)

Основные свойства векторного произведения:

1. Векторное произведение равно нулю, если векторы a и b коллинеарны или какой-либо из перемножаемых векторов является нулевым.

2. При перестановке местами векторов сомножителей векторное произведение меняет знак на противоположный (см. рисунок):

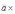
Векторное произведение не обладает свойством переместительности.

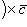
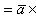
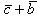
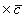3. (распределительное свойство)

Выражение векторного произведения через проекции векторов a и b на координатные оси прямоугольной системы координат дается формулой:

(27)

которую можно записать с помощью определителя

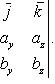(28)

Проекции векторного произведения на оси прямоугольной системы координат вычисляются по формулам

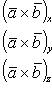
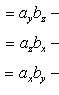
(29)

и тогда на основании (4)

(30)

Механический смысл векторного произведения состоит в следующем: если вектор - сила, а вектор есть радиус-вектор точки приложения силы, имеющий свое начало в точке O, то момент силы относительно точки O есть вектор, равный векторному произведению радиуса-вектора точки приложения силы на силу , т. е.