19. Угол между двумя прямыми. Условие параллельности и пе4. Условия параллельности двух прямых:

Условия параллельности двух прямых:

а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов: k1 = k2.

б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

Условия перпендикулярности двух прямых:

а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.

Определение. Если заданы две прямые y = k1x + b1, y = k2x + b2, то острый угол между этими прямыми будет определяться как

Две прямые параллельны, если k1 = k2.

Две прямые перпендикулярны, если k1 = -1/k2.

Теорема. Прямые Ах + Ву + С = 0 и А1х + В1у + С1 = 0 параллельны, когда пропорциональны коэффициенты А1 = lА, В1 = lВ. Если еще и С1 = lС, то прямые совпадают.

Координаты точки пересечения двух прямых находятся как решение системы уравнений этих прямых.

Если уравнения прямой заданы в общем виде

A1x + B1y + C1 = 0,

A2x + B2y + C2 = 0,

угол между ними определяется по формуле

20. Расстояние от точки до прямой на плоскости.

Расстояние от точки до прямой

Теорема. Если задана точка М(х0, у0), то расстояние до прямой Ах + Ву + С =0 определяется как

Доказательство. Пусть точка М1(х1, у1) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М1:(какое –то уравнение)))

Координаты x1 и у1 могут быть найдены как решение системы уравнений:

Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М0 перпендикулярно заданной прямой.

Если преобразовать первое уравнение системы к виду:

A(x – x0) + B(y – y0) + Ax0 + By0 + C = 0,

то, решая, получим:

Подставляя эти выражения в уравнение (1), находим:

Теорема доказана. Пример. Определить угол между прямыми: y = -3x + 7; y = 2x + 1.

k1 = -3; k2 = 2 tgj = ; j = p/4.

Пример. Показать, что прямые 3х – 5у + 7 = 0 и 10х + 6у – 3 = 0 перпендикулярны.

Находим: k1 = 3/5, k2 = -5/3, k1k2 = -1, следовательно, прямые перпендикулярны.

Пример. Даны вершины треугольника А(0; 1), B(6; 5), C(12; -1). Найти уравнение высоты, проведенной из вершины С.

Находим уравнение стороны АВ: ; 4x = 6y – 6; 2x – 3y + 3 = 0;

Искомое уравнение высоты имеет вид: Ax + By + C = 0 или y = kx + b.

k = . Тогда y = . Т.к. высота проходит через точку С, то ее координаты удовлетворяют данному уравнению: откуда b = 17. Итого: .

Ответ: 3x + 2y – 34 = 0.

21. Линии второго порядка на плоскости.

Определение. Линией (кривой) второго порядка называется линия общее уравнение которой имеет следующий вид:

Уравнение второй степени вида (не содержащее члена c произведением координат) называется пятичленным уравнением кривой второго порядка. Оно определяет на плоскости эллипс, гиперболу и параболу (с возможными случаями распада и вырождения этих кривых) с осями симметрии, параллельными осям координат, в зависимости от знака произведения коэффициентов А и .

Окружность является простейшей кривой второго порядка. Определение. Окружностью радиуса с центром в точке называется множество всех точек Μ плоскости, удовлетворяющих условию

П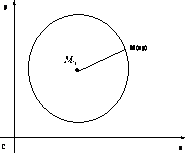 усть точка в прямоугольной системе координат имеет координаты , , а – произвольная точка окружности.

Тогда из условия получаем уравнение , отсюда

– каноническое уравнение окружности.

Этому уравнению удовлетворяют координаты любой точки окружности и не удовлетворяют координаты никакой точки не лежащей на окружности.

Если , , то получим уравнение окружности в центром в начале координат .

Эллипс Пусть на плоскости даны две точки и , которые называются фокусами эллипса.

Определение. Эллипсом называется геометрическое место точек плоскости, сумма расстояний каждой из которых до двух заданных фокусов есть величина постоянная.

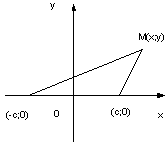
Введем систему координат на плоскости так, чтобы точки и имели бы координаты соответственно и Пусть точка плоскости такова, что . Числа c и a фиксированные положительные. Таким образом, и, как следует из неравенства треугольника, . Причем равенство здесь выполняется, только в том случае, когда лежит между и , и этот случай мы рассматривать не будем.

Перепишем равенство в координатах: Это уравнение и есть уравнение эллипса в выбранной системе координат. Единственное, что осталось – это избавиться от иррациональности и привести к виду, называемому каноническим уравнением эллипса. Для этого перенесем один из радикалов в правую часть и возведем обе части равенства в квадрат: или, после очередных преобразований, получаем

Так как , то .

Обозначив , запишем уравнение в виде

Разделим обе части равенства на , получим каноническое уравнение эллипса:

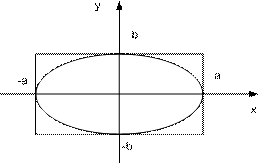
Каноническое уравнение эллипса содержит x и y только в четных степенях, поэтому если точка принадлежит эллипсу, то ему также принадлежат точки , , . Отсюда следует, что эллипс симметричен относительно осей и , а также относительно точки , которую называют центром эллипса.

Найдем точки пересечения эллипса с осями координат.

Пусть , тогда находим две точки и , в которых ось пересекает эллипс, а при ось пересекает эллипс в точках и .Точки , ,, и называют вершинами эллипса. Отрезки называют соответственно большая и малая оси эллипса. Числа – большая и малая полуоси. Так как в каноническом уравнении эллипса сумма равна единице, то каждое из слагаемых не превосходит единицы, следовательно имеют место неравенства

или

а это значит, что все точки эллипса находятся внутри прямоугольника, образованного прямыми . А так же при возрастании одного слагаемого другое будет уменьшаться, поэтому при увеличении уменьшается , и наоборот. Поэтому форма эллипса – овальная замкнутая кривая

От отношения зависит форма эллипса, если , то эллипс становится окружностью.

Пусть , тогда фокусы и находятся на оси на расстоянии от начала координат.

Определение. Отношение половины расстояния между фокусами к большой полуоси

называется эксцентриситетом эллипса b и характеризует степень сжатия, причем , так как .

Поскольку , то можно записать , отсюда , а это значит, что чем меньше эксцентриситет, тем менее сплющенным будет эллипс.

Если взять , то эллипс превращается в окружность.

Расстояния от точки эллипса до его фокусов называют фокальными радиус-векторами, которые определяются формулами: и .

Если же , то большая ось и фокусы и находятся на оси ,

эксцентриситет ,

фокальные радиус-векторы и .

Коэффициент сжатия:

Параметрическое уравнение эллипса имеет вид:

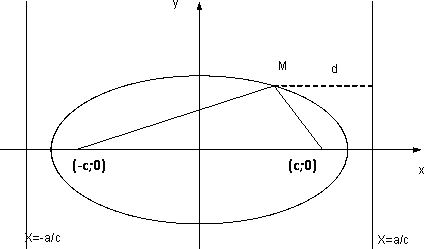
Определение. Прямые называют директрисами.

Теорема. Если – расстояние от любой точки эллипса до какого-либо фокуса, а расстояние от этой же точки до соответствующей этому фокусу директрисы, то отношение – постоянная величина, равная эксцентриситету эллипса,