15. Функция распределения двумерной случайной величины и её свойства

Функцией распределения   двумерной случайной величины   называется вероятность произведения событий   и  , определенная для любых вещественных  :  . (1)

Геометрический смысл равенства (1): функция   есть вероятность того, что случайная точка   попадет в бесконечный квадрат с вершиной в точке  ; точка   будет левее и ниже этой вершины.

Свойства двумерной функции распределения

1.  .

2.  ,  . ,  F(- ∞, -∞) = 0

4.  ;

. (2)

5.   неубывающая функция по каждому из своих аргументов при фиксированном другом аргументе.

Формулы (2) означают, что из функции распределения двумерной случайной величины можно получить функции распределения ее одномерных компонент.Используя функцию распределения, можно найти вероятность попадания случайной точки в прямоугольник  :

.

16. Двумерная плотность вероятности и её свойства. Нахождение функции распределения системы по известной плотности распределения

Дискретная двумерная случайная величина

Двумерная случайная величина   называется дискретной, если множество ее значений   – конечное или счетное.

Закон распределения вероятностей двумерной дискретной случайной величины   можно задать формулой

. (3)

Непрерывная двумерная случайная величина

Двумерная случайная величина называется   непрерывной, если существует такая неотрицательная функция  , называемая двумерной плотностью вероятности, что вероятность попадания случайной величины   в область   равна двойному интегралу от плотности по этой области(вторая смешанная частная производная от функции распределения ):

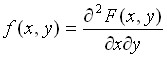
Свойства двумерной плотности вероятности

1.   неотрицательная функция и определена на всей плоскости  .

2. 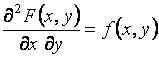  в каждой точке непрерывности плотности.

3. 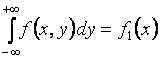 ;  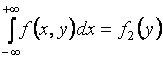. (9)

4.  . (10)

Формулы (9) означают, что из плотности распределения двумерной случайной величины можно получить   – плотности распределения ее одномерных компонент.

Зная плотность совместного распределения , можно найти функцию распределения F(x,y) по формуле :

F(x,y)=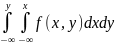

17. Зависимые и независимые случайные величины. Корреляционый момент. Коэффициент корреляции

Случайные величины   называются независимыми, если независимыми являются события   и   для любых вещественных  . В противном случае величины называютсязависимыми.

Общее необходимое и достаточное условие независимости двух случайных величин:

, (11)

где   – любые вещественные числа.

Необходимое и достаточное условие независимости двух непрерывных случайных величин:

, (12)

где   – любые вещественные числа.

Если условные плотности распределения случайных величин   и   равны их безусловным плотностям, то такие величины независимы.

Необходимое и достаточное условие независимости двух дискретных случайных величин:

, (13)

где  ;  .

Числовые характеристики системы двух случайных величин

Средние значения (математические ожидания)   определяют точку  , называемую центром совместного распределения вероятностей или центром рассеивания.

Корреляционный момент и коэффициент корреляции

Числовыми характеристиками связи между случайными величинами являются корреляционный момент и коэффициент корреляции.

Корреляционным моментом  , иначе – ковариацией двух случайных величин  называется математическое ожидание произведения отклонений этих случайных величин от их математических ожиданий:

. (14)

Формулы для вычисления корреляционного момента  :

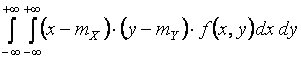 (15)

– для непрерывных случайных величин,

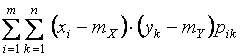 (16)

– для дискретных случайных величин.

Коэффициентом корреляции   двух случайных величин   называется отношение их корреляционного момента к произведению средних квадратических отклонений:

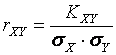. (17)