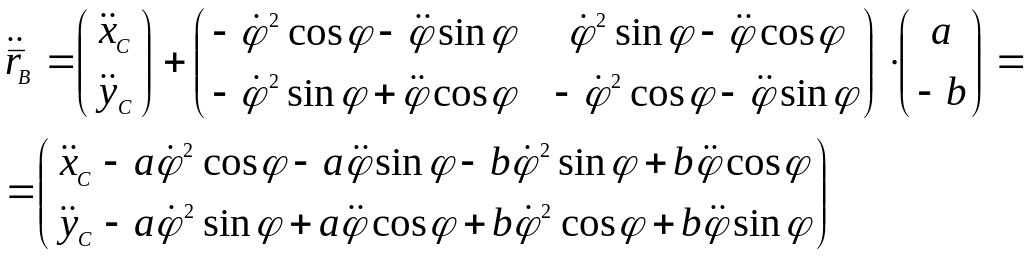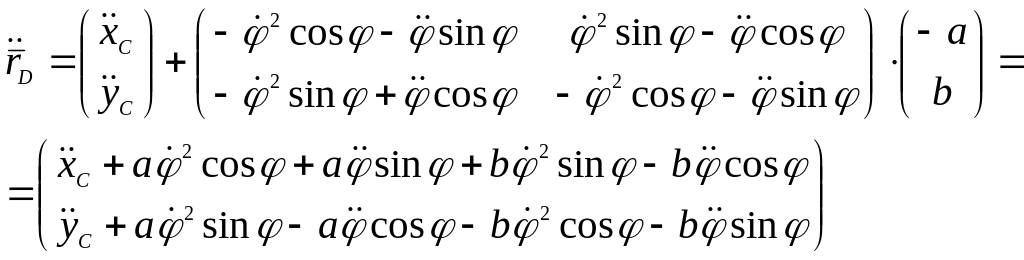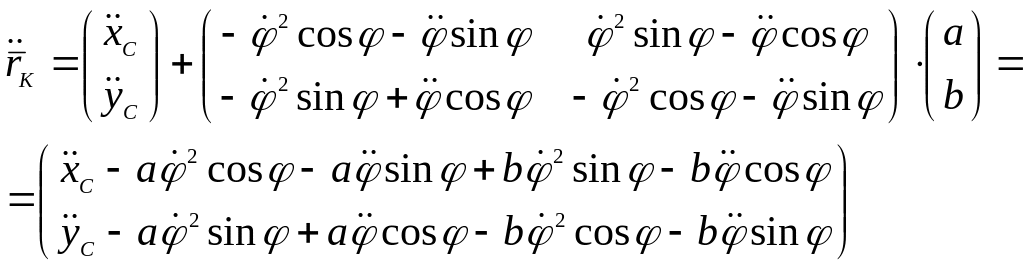2 Исследовательский раздел
Требуется разработать математическую модель прыгающего робота, алгоритм численного моделирования его движения.
2.1 Описание разрабатываемой конструкции
После анализа существующих конструкций роботов, перемещающихся с отрывом от поверхности, была разработана конструкция прыгающего робота, изображенная на рисунке 2.1.
сделать конструкцию робота, дорисовать корпус
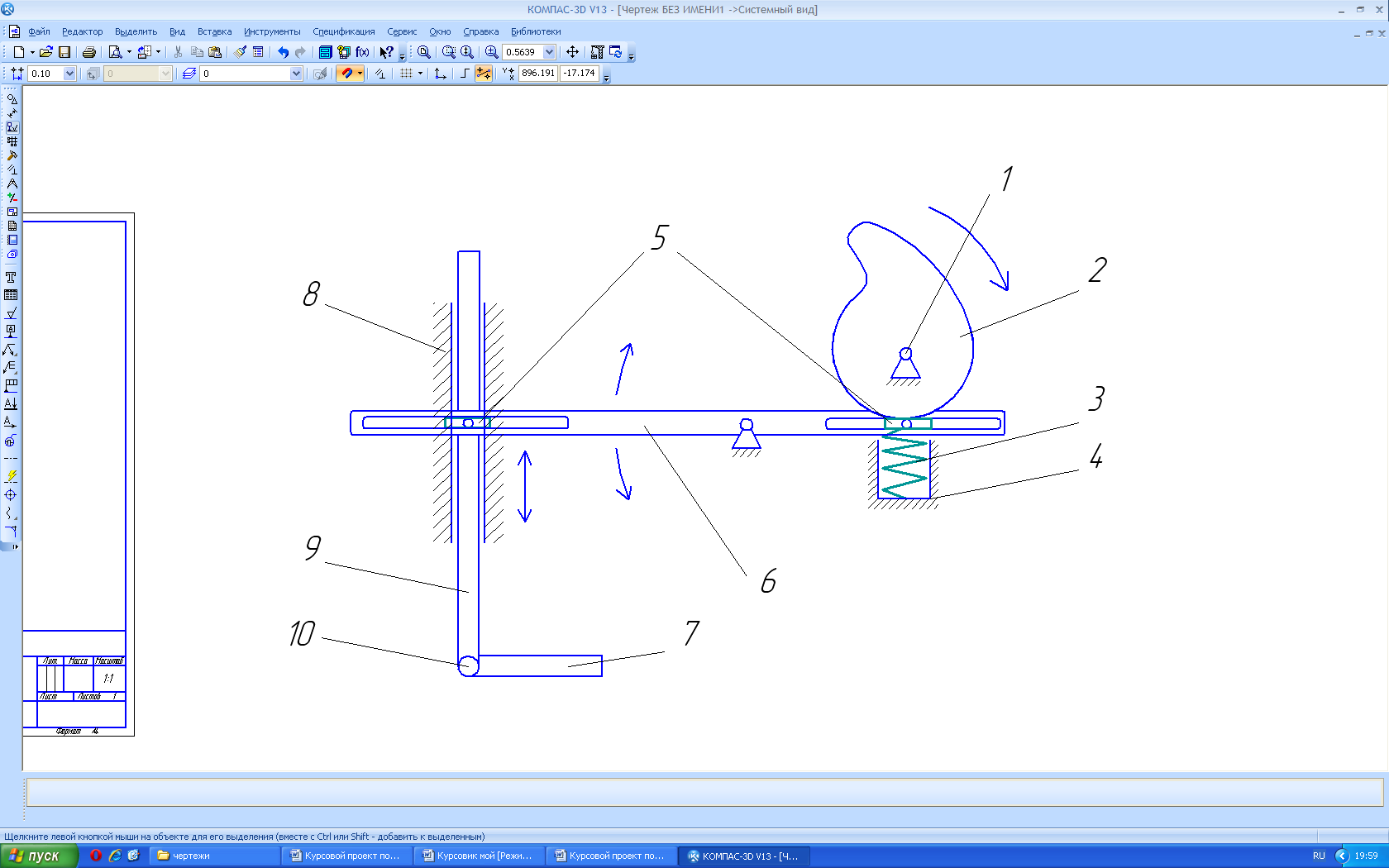
Рисунок 2.1 Структурная схема прыгающего робота
Конструкция представляет собой привод поворота кулачка (1), который, вращая кулачок (2), взводит пружину сжатия (3), которая закреплена в цилиндре (4). В момент, когда происходит прощелкивание кулачка, энергия накопленная в пружине придает скорость вращения кулисе (6), которая соединена с пружиной ползуном (5). Другой конец кулисы соединен с ногой (9), которая соединена с ней при помощи ползуна и движется по направляющим (8).
Следовательно, после прощелкивания энергия от пружины через кулису передается ноге, которая перемещаясь по направляющим придает корпусу робота скорость и ускорение. После чего и происходит сам прыжек.
Позиционирование ноги робота происходит при помощи двух приводов: привода поворота ноги относительно ступни (10) (7 - ступня) и привод поворота корпуса относительно ноги (на данной схеме нее показан).
Было проведено проектирование конструкции (рис. 4) ноги двуногого прыгающего робота.
2.1 Кинематика системы
Будем рассматривать движение робота в плоскости, в которой введем две системы координат: абсолютную неподвижную Оху и относительную – Сх1у1, которая жестко связана с корпусом робота так, что начало координат С совпадает с положением центра масс корпуса, ось Сх1 параллельна стороне АВ. Угол φ определяет поворот системы координат Сх1у1 относительно Оху (рисунок 2.2). Будем считать, что корпус робота является абсолютно твердым телом, имеющим форму прямоугольника с размерами 2а×2b, масса m которого сосредоточена в центре симметрии – точке С.
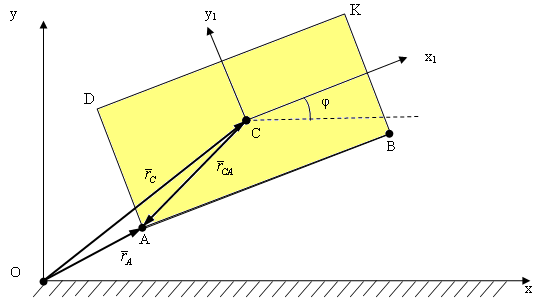
Рисунок 2.2 Кинематическая схема робота
Будем считать, что каждый прыжок робота включает в себя три фазы: разгон, полет и приземление. В первой и третьей фазах робот взаимодействует с опорной поверхностью, в фазе полета робот движется с отрывом от поверхности.
Обобщенными координатами являются проекции хС и уС положения центра масс корпуса на оси абсолютной системы координат и угол φ поворота корпуса.
При разработке математической модели будем считать, что прыжок робота происходит из начального положения, при котором его корпус контактирует с шероховатой горизонтальной поверхностью в точках А и В, причем в точке А при контакте с поверхностью действуют силы нормальной реакции NА и сухого трения Ffr, а в точке В – только нормальная реакция NВ.
Положим, что при приземлении устройства происходит абсолютно неупругий удар, а в первой точке приземления возникают силы нормальной реакции и сухого трения, после чего происходит поворот корпуса относительно этой неподвижной точки до тех пор, пока вторая точка корпуса не коснется поверхности. При этом во второй точке опоры будет возникать только нормальная реакция.
Рассчитаем координаты, скорости и уравнения для точек А, В и С.
Радиус-вектор точки C в абсолютной системе координат определяется как:
,
Координаты
радиуса-вектора
рассчитываем по следующей формуле:
,
где
Т
- матрица поворота, обеспечивающая
перевод координат, определенных в
системе
,
в систему
;
-
радиус-вектор точки A
в относительной системе координат.
Матрица поворота Т определяется как:
.
Радиус-вектор
равен:
где
a
и b
- расстояния от точки C
до точки A
вдоль осей
и
соответственно.
Абсолютный радиус-вектор точки А равен:
Координаты абсолютных радиусов-векторов точек В, D и К найдем аналогичным образом.
Относительные радиусы-векторы точек имеют вид:
,
,
.
Абсолютные радиусы-векторы запишем следующим образом:
,
,
.
Определим скорости центра масс корпуса – точки С и точек А, В, D, К как производные соответствующих радиусов-векторов.
Вектор
скорости точки C
определяем как:
где
и
- проекции вектора скорости точки C
на оси абсолютной системе координат.
Скорость точки A рассчитаем по следующей формуле:
,
где
- вектор скорости точки A
в относительной системе координат.
Производная матрицы поворота Т выглядит следующим образом:
Вектор скорости точки A в относительной системе координат имеет вид:
Вектор абсолютной скорости точки А запишем как:
Векторы скоростей точек B, D и К определяем аналогичным образом. Векторы относительных скоростей всех точек нулевые.
,
.
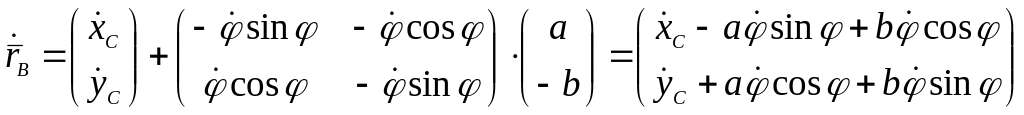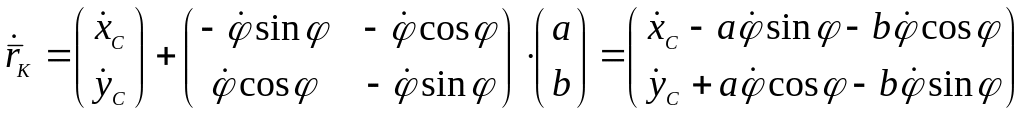Вектор
ускорения точки С
определяется как:
где
и
- проекции вектора ускорения точки С
на оси абсолютной системе координат.
Ускорение точки A рассчитаем по формуле:
,
Вторая производная матрицы поворота Т выглядит следующим образом:
Тогда вектор ускорения точки А имеет вид:
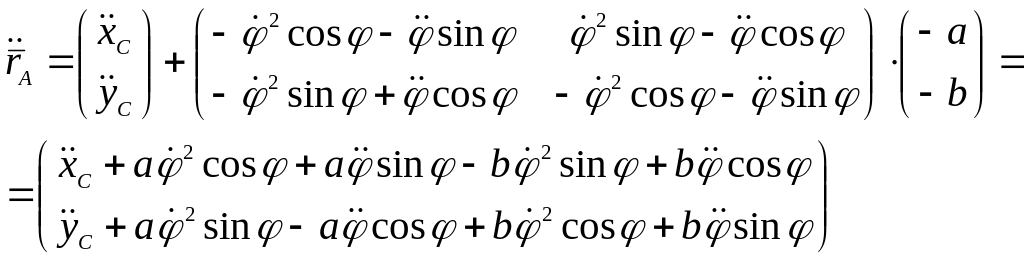
Абсолютные ускорения точек В, D и К равны:
