Глава 6

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

#1

БИЛЕТ 1

ОСНОВНЫЕ ПОНЯТИЯ О ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЯХ

О1

ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЕМ называется уравнение, в которое, кроме неизвестных функций и их аргументов входят производные неизвестных функций или дифференциалы неизвестных функций и их аргументов.

О2

Дифференциальное уравнение, содержащее неизвестные функции одного аргумента, называется ОБЫКНОВЕННЫМ ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЕМ, а дифференциальные уравнения, содержащие неизвестные функции нескольких аргументов, называются ДИФФЕРЕНЦИАЛЬНЫМИ УРАВНЕНИЯМИ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ.

Будем рассматривать обыкновенные дифференциальные уравнения с одной неизвестной функцией

Они имеют вид

(1)

О3

ПОРЯДКОМ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ называется порядок входящих в него производных

Уравнение (1) – уравнение n-го порядка

О4

РЕШЕНИЕМ дифференциального уравнения называется функция ,если при подстановке этой функции и ее производных в уравнение, оно превращается в тождественное.

О5

Процесс нахождения решений дифференциального уравнения называется ИНТЕГРИРОВАНИЕМ этого уравнения

При интегрировании дифференциального уравнения может получиться не решение , а некоторое соотношение между функцией и ее аргументом х, не решенное относительно у, т.е., тогда получается решение в неявном виде. Такое соотношение между у и х называется интегралом дифференциального уравнения.

О6

ИНТЕГРАЛОМ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ называется такое соотношение, не содержащее производных искомой функции, из которого дифференциальные уравнения вытекают как следствия.

Пример

Дано дифференциальное уравнение

Функция ,(c=const) - это его решение. Так, представляя в уравнении эту функцию и ее производную

Соотношение х=с является интегралом этого уравнения, т.к., дифференцируя его, получаем само уравнение

БИЛЕТ 2

#2

ДИФФЕРЕНЦИАЛЬНО УРАВНЕНИЕ 1-ГО ПОРЯДКА (ОСНОВНЫЕ ПОНЯТИЯ)

Уравнение

(2)

Содержащее аргумент х, неизвестную функцию и ее производную, это дифференциальное уравнение первого порядка. Решая соотношение (2) относительно у’, мы можем написать это уравнение в виде

(3)

Или же

Обозначим f(x;y)= , тогда получим

. Т.е. дифференциальное уравнение первого порядка можно выразить через дифференциал dy и dx функции и ее аргументов.

(5)

В простейшем случае функция может не зависеть от у, тогда уравнение (3) записывается в виде

(6)

По определению неопределенного интеграла решение дифференциального уравнения будет иметь вид

, где с – произвольная постоянна

В общем случае, когда зависит и от х и от у решение уравнения (3) будет содержать произвольную постоянную, т.е. имеет вид

(7)

Формулы (7) описывают множество решений, отличающихся друг от друга значением постоянной с. Такое множество решений называется СЕМЕЙСТВОМ решений дифференциального уравнения

О7

СЕМЕЙСТВО РЕШЕНИЙ дифференциального уравнения (3), отличающихся друг от друга значениями постоянной с, называются ОБЩИМ РЕШЕНИЕМ этого уравнения, а уравнение ,не решенное относительно у, из которого дифференциальное уравнение вытекает как следствие, называется ИНТЕГРАЛОМ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ. Значит, интеграл дифференциального уравнения содержит решение в неявном виде.

О8

Решение или интеграл дифференциального уравнения при определенном значении постоянной называется ЧАСТНЫМ РЕШЕНИЕМ или ЧАСТНЫМ ИНТЕГРАЛОМ дифференциального уравнения.

О9

Решение дифференциального уравнения, не получающееся из общего решения ни при каких значениях постоянной с, называется ОСОБЫМ РЕШЕНИЕМ.

БИЛЕТ 3

ДИФФЕРЕНЦИАЛЬНО УРАВНЕНИЕ 1-ГО ПОРЯДКА(ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ЭТИХ УРАВНЕНИЙ И ИХ РЕШЕНИЙ)

Рассмотрим геометрический смысл дифференциального уравнения 1-го порядка и геометрический смысл его решения

Если рассматривать х и у как координаты точки на плоскости, то дифференциальное уравнение (3) задает в каждой точке M(x;y) функцию f(x;y), но ,т.е. в соответствие с геометрическим смыслом производной, в каждой точке области определения функции задается направление касательной графику некоторой функции . Оно является решением дифференциального уравнения. Таким образом, решение дифференциального уравнения, т.е. линия - это такая линия, которая в каждой точке имеет касательную, угловой коэффициент которой равен n!r уравнения (3). Такая линия называется интегральной кривой данного дифференциального уравнения и описывает его частные решения. Множество функция , различающихся значениями постоянной с, дает множество интегральных кривых, называемое семейством интегральных кривых, соответствующих общему решению дифференциального уравнения.

| | | | | | для того, чтобы из семейства интегральных кривых выделить определенную интегральную кривую, необходимо найти соответствующее значение постоянной с, а для этого нужно указать, через какую точку должна проходить эта интегральная кривая

Для выделения частного решения их общего решения задается начальное условие, т.е. (8) ( , которое обозначает, через какую точку должна проходить данная интегрированная кривая

Через одну и ту же точку иногда может проходить не одна, а две интегральных прямых, одна из которых принадлежит семейству интегральных прямых, т.е. дает частное решение, а другая не принадлежит этому семейству, т.е. дает особое решение дифференциальной уравнения

БИЛЕТ 4

ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЕМ С РАЗДЕЛЕННЫМИ ПЕРЕМЕННЫМИ

#3

ДИФФЕРЕНЦИАЛЬНЫЕ ЦРАВНЕНИЯ С РАЗДЕЛЕННЫМИ И РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ

О10

Если дифференциальном уравнении вида (5) коэффициенты при х зависят только от х, а коэффициенты при у зависят только от у, т.е.

9)

То такое уравнение называется ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЕМ С РАЗДЕЛЕННЫМИ ПЕРЕМЕННЫМИ

Общий интеграл такого уравнения имеет вид

(10)

Действительно, дифференцируя обе части этого выражения получаем уравнение (9)

’

C’=0

С учетом этого получаем уравнение (9). Вместо неопределенных интегралов можно использовать интегралы с переменными верхними пределами.

Тогда интеграл дифференциального уравнения запишется в виде

(11)

Если дано начальное условие (8), то полагая верхние пределы получаем С=0, т.е. частный интеграл уравнения будет иметь вид

(12)

БИЛЕТ 5

ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЕМ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ

О11

Если в дифференциальном уравнении вида (5) коэффициенты при dx и при dy являются произведениями функции, зависящей только от х, на функцию зависящую только от у, т.е.

3)

То такое уравнение называется УРАВНЕНИЕМ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ

Если , то разделив уравнение (13) почленно на получим уравнение с разделяющимися переменными

(14)

Следовательно, если общий интеграл имеет вид

(15)

Или (16)

А частный интеграл, соответствующий начальному условию

имеет вид

(17)

Мы полагаем, что и при этом могли потерять решения. Поэтому мы должны проверять, не содержат ли равенства

Потерянные особые решения

БИЛЕТ 6

#4

ОДНОРОДНОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ 1-ГО ПОРЯДКА

О12

Функция M(x;y) называется ОДНОРОДНОЙ ФУНКЦИЕЙ К-ОГО ПОРЯДКА или ИЗМЕРЕНИЯ, если

M(tx;ty)=tM(x;y)(18)

О13

Дифференциальное уравнение вида (5) называется ОДНОРОДНЫМ, если коэффициенты при dx и dy являются однородными функциями одного и того же порядка

M(tx;ty)= (18’)

N(tx;ty)= (18’)

Если дано уравнение вида (3), где f(x;y)= , то

О13’

Дифференциальное уравнение вида (3) называется однородным если функция f(x;y) – однородная нулевого измерения

f(tx;ty)=f(x;y)

однородное дифференциальное уравнение сводится к уравнению с разделяющимися переменными путями подстановки

, т.е.

#4

ОДНОРОДНОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ 1-ГО ПОРЯДКА

Действительно, подставляя в уравнение (3), т.е.

, получаем , с учетом того, что f(x;tx)=f(1;t)

т.е. . Разделив на х [t-f(1;t)], получаем уравнение с разделяющимися переменными

БИЛЕТ 7

#5 ДИФФЕРЕНЦИАЛЬНОЕ УР-Е В ПОЛНЫХ ДИФФЕРЕНЦИАЛАХ

Опр 14. Если левая часть дифференциального уравнения M(x;y)dx+N(x;y)dy=0(5) представляет собой дифференциал некоторой функции U(x;y), т.е. dU(x;y)=M(x;y)dx+N(x;y)dy(19), то уравнение (5) называется уравнением в полных дифференциалах.

Согласно уравнению полного дифференциала, dU(x;y)= dx+ dy(20)

Сравнивая 18 и 19 находим =M(x;y); =N(x;y) (21)

Отсюда следует, что = ; =

Смешанные производные равны, следовательно = (22)

Формула 22 – условие того, что уравнение 5 – это уравнение в полных дифференциалах. Сравнивая 19 и 5 находим dU(x;y)=0, следовательно общий интеграл уравнения 5 имеет вид: U(x;y)=c, где c=const (23)

Интегрируя уравнение 21 находим: U(x;y)= +C1(y) (24)

U(x;y)= +C2(x)

Из этих формул следует: C1(y)=U(x0;y); C2(x)=U(x;y0) (25)

Из формул 24 и 25 получаем:

U(x;y)= +

U(x;y)= + (26)

Т.о., находим 2 формы для общего интеграла ур-я 5 (используя формулы 23 т 26):

+ =С (27)

+ =С (28)

БИЛЕТ 8

#6 ИНТЕГРИРУЮЩИЙ МНОЖИТЕЛЬ

Опр 15

Если при умножении дифференциального уравнения 5 на мелот. множитель M(x;y)M(x;y)dx+M(x;y)N(x;y)dy=0 (29) в полных дифференциалах, то множитель M(x;y)называется интегрирующим множителем.

Рассмотрим 2 частных случая: когда имеет интегрирующий множитель зависит только от у и когда этот множитель зависит только от х.

Согласно условию 22 получаем

[M(x;y)M(x;y)]= [M(x;y)N(x;y)], т.е. M(x;y) +M(x;y) =N(x;y) +M(x;y)

В первом случае M(x;y)=M(x)т.е. =0, тогда M(x;y) -M(x) =N(x;y) , т.е.

- = =Ф1 (x), т.е. =Ф1(x)dx => = dx=> ln M(x)= dx=>M(x)=e в степени dx (31)

Во втором случае M(x;y)=M(y), т.е. =0, тогда получаем:

=Ф2(y), т.е.

=-Ф2(y), M(y)=e в степени dy (32)

БИЛЕТ 9

#7

ЛИНЕЙНОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ПЕРВОГО ПОРЯДКА

Опр 16

Дифференциальное уравнение вида y’+P(x)y=Q(x) (33), содержащее неизвестную функцию y=f(x) и ее производную у’ в первых степенях, называется линейным дифференциальным уравнением 1 порядка. Если Q(x)=0, то уравнение y’+P(x)y=0 (34) называется однородным линейным дифференциальным уравнением, а при Q(x) = 0 уравнение 33 называется неоднородным линейным дифференциальным уравнением

Сначала найдем решение уравнения 34, т.е.

+P(x)y=0 dy+P(x)ydx=o. Разделим на у, получим уравнение с разделенными переменными: +P(x)dx=0

Решаем его: + dx=ln x

Lny = lnc – dx

y=Ce в степени - dx (35)

Получаем общее решение линейного однородного уравнения. Будем искать решение линейного неоднородного уравнения в том же виде, но вместо постоянной С введем функцию С(х), т.е.

y=C(x)e в ст. - dx

y’=C’(x)e в ст. - dx+C(x)[e в ст. - dx]=C’(x)e в ст. - dx-C(x)P(x)e в ст. - dx

подставим y и y’ в 33:

C’(x)e в ст. - dx- C(x)P(x)e в ст. - dx + C(x)P(x)e в ст. - dx=Q(x)

Q(x)e ст. + dx=C’(x), т.е., интегрируя, находим соответствующее решение уравнения 33, т. К. C(x)= e в ст. dx dx+c, т.е. это общее решение имеет вид:

y=e в ст. - dx[C+ e ст. dx dx] (36)

Заменяя неопределенные интегралы интегралами с переменными верхними пределами, это общее решение можно записать в виде: y=e в ст. – dx [C+ e в ст. dx” dx’] (36’)

Найдем частное решение при начальном условии y| (внизу написано x=x0)=y0. Подставляя в (36’) x=x0, y=y0, находим: С=y0

Следовательно частное решение линейного неоднородного уравнения имеет вид y=e в ст. - dx’[y0+ e в ст. dx” dx’] (37)

БИЛЕТ 10

УРАВНЕНИЕ БЕРНУЛЛИ

К линейному неоднородному уравнению сводится уравнение Бернулли:

y’+P(x)y=Q(x)yⁿ (38)

если n = 0, то это уравнение 33 (y’+P(x)y=Q(x)), а если n=1, то это однородное линейное уравнение y’+[P(x)-Q(x)]y=0

в остальных случаях можно сделать замещение переменной:

z=y^1-n, тогда z’=(1-n)y^-ny’. Умножая обе части уравнения 38 на (1-n)y^-1, получаем (1-n)y^-ny’+(1-n)P(x)-n y=Q(x)(1-n), т.е. для переменной z получаем линейное неоднородное уравнение:z’+(1-n)p(x)z=(1-n)Q(x) (39).

БИЛЕТ 11

# 8

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ, ДОПУСКАЮЩИЕ ПОНИЖЕНИЕ ПОРЯДКА.

1. Уравнение вида

y⁽ⁿ⁾=f(x) (40)

интегрируется путем последовательного интегрирования

y^(n-1)= dx+C₁

y^(n-2)= dx+C₁x+C₂

y^(n-1)= dx+C₁x²/2+C₂+C₃

2. Уравнение вида

F(x;y’;y”)=0 (41),

не содержащее у в явном виде. Подстановкой y’=p, y”=dy’=dp/dx, получаем уравнение 1 порядка

F(x,p,dp/dx)=0 (42),

интегрируя которое, находим функцию р(х;с₁). Так как dy/dx =p(x;c₁), то интегрируя это выражение, находим функцию

y=f(x;c₁;c₂)

3. Уравнение вида

F(y;y’;y”)=0 (43),

не содержащее х. В этом случае аргументом будем считать у, а искомой функцией функцию у=р, тогда

y”=dy’/dx=dy’dy/dydx=(dp/dy)P, т.е. уравнение (43) приобритает вид

F(y; p; p(dp/dy)=0 (44)

Решая уравнение (44), находим функцию p(y;c), а решая уравнение dy’/dx=p(y;c₁)_, находим искомую функцию

у=f(x;c₁;c₂)

Таким образом, у нас происходило понижение порядка дифференциального уравнения.

БИЛЕТ 12

# 9

ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ И ИХ ОСНОВНЫЕ СВОЙСТВА

О 17

ЛИНЕЙНЫМ ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЕМ n-ОГО ПОРЯДКА называется уравнение вида

y⁽ⁿ⁾+p₂(x)y^(n-1)+p₂(x)y^(n-2)+…+p_n+1(x)y’+p_n(x)y=Q(x) (45), в которое неизвестная функция у и ее производные входят линейно, т.е. в первых степенях. Если Q(x)=0, то уравнение называется ЛИНЕЙНЫМ ОДНОРОДНЫМ, а если Q(x)≠0- ЛИНЕЙНЫМ НЕОДНОРОДНЫМ

О18

Если решения y₁,y₂,y₃…y_x, связанные соотношением

α₁y ₁+α ₂y ₂+…+α _xy _x=0 (46),

где α ₁,α ₂… α_n – постоянные коэффициенты, среди которых имеются неравные нулю, то эти решения называются ЛИНЕЙНО ЗАВИСИМЫМИ. Если же такого соотношения тождественного относительно х не существует, то эти решения называются ЛИНЕЙНО НЕЗАВИСИМЫМИ.

Если решения y₁, y₂… y_к линейно зависимы, то решение перед которым в соотношении (46) стоит неравный 0 коэффициент, то это решение можно выразить через остальные решения. Например, если α₁≠0, то y₁=-1; α₂(α₂y₂+… α_кy _к)

Если же решения линейно независимы, то они не выражаются друг через друга, т.е. число линейно независимых решений уменьшить нельзя.

Для упрощения записи обозначим

L(y)=y⁽ⁿ⁾+p₁(x)y^(n-1)+p₂(x)y^(n-2)+…+p_n-1(x)y’+p_n(x)y (47)

тогда уравнение (45) записывается в виде L(y)=Q(x) (48)

Т 1

Если у₁, у₂…у_n линейно независимые частные решения однородного линейного дифференциального уравнения L(y)=0, то его общее решение имеет вид

y=c₁y₁+c₂y₂+…+c_ny_n (49), где с₁,c₂…c_n – произвольные постоянные.

Доказательство: т.к. производная суммы функций равна сумме производных слагаемых, а постоянный множитель можно выносить за знаки производных, то мы имеем

L(y)=L(c₁,y₁+c₂y₂+…c_ny_n)=c₁L(y₁)+c₂L(y₂)+…+c_nL(y₂), а т.к. у₁,у₂…у_n – это частные решения однородного линейного дифференциального уравнения L(y)=0, то L(y₁)=0, L(y₂)=0…L(y_n)=0, следовательно у - решение уравнения L(y)=0.

Так как частные решения являются линейно независимыми, т.е. ни одно из них не выражается через другие решения и следовательно число произвольных постоянных не может быть уменьшено, а число произвольных постоянных совпадает с порядком дифференцированного уравнения, следовательно, выражение (49) является общим решением линейного однородного дифференциального уравнения.

Теорема доказана.

Т 2

Если у₁,у₂…у_n линейно независимые частные решения однородного линейного дифференциального уравнения L(y)=0, а функция U(x) является каким-либо частным решением соответствующего линейного неоднородного уравнения (48), т.е.

L(U)=Q(x), то общее решение линейного неоднородного уравнения и какого-либо частного решения линейного неоднородного уравнения, т.е.

y=c₁y₁+c₂y₂+…+c_ny_n+U (50)

Доказательство

По условию L(c₁,y₁+c₂y₂+…c_ny_n)=0, L(U)=Q(x) (51), следовательно, L(c₁,y₁+c₂y₂+…c_ny_n+U)= L(c₁,y₁+c₂y₂+…c_ny_n)+L(U)+Q(x), т.е. (49) – это решение линейного неоднородного уравнения. Число постоянных с₁,c₂…c_n, равное порядку уравнения не может быть уменьшено, следовательно, это решение является общим.

БИЛЕТ 13

#10

ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ С ПОСТОЯННЫМ КОЭФФИЦИЕНТОМ

Рассмотрим дифференциальное уравнение вида y⁽ⁿ⁾+p₁y^(n-1)+p₂y^(n-2)+…+p_n-1y’+p_ny=Q(x) (52), где p₁=const, p₂=const… p_n-1=const, p_n=const.

Соответствующее линейное однородное уравнение имеет вид

y⁽ⁿ⁾+p₁y^(n-1)+p₂y^(n-2)+…+p_n-1y’+p_ny=0 (53).

Будем искать его решение в виде

y=e^x

тогда у’=re^rx, y”=re^rx,… y^(n-2)=r^(n-2)e^rx, y^(n-1)=r^n-1e^rx, y⁽ⁿ⁾=rⁿe^rx

Подставляя это выражение в выражении (53) и сокращая на е^nx≠0 получаем алгебраическое уравнение n-ой степени

rⁿ+p₁r^n-1+p₂r^n-2+…+p_n-1r+p_n=0 (54),

называемое ХАРАКТЕРИСТИЧЕСКИМ УРАВНЕНИЕМ. Следовательно в рассматриваемом случае решение дифференциального уравнения сводится к решению алгебраического уравнения (54)

алгебраическое уравнение n-ой степени имеет n решений r, r₂, r_3… r_n. Если все эти решения различны, мы получаем n линейно независимых частных решений дифференциального уравнения (53)

y₁=e^r1x+c₂e^r2x+…+c_ne^rnx (55)

#11 ЛИНЕЙНЫЕ ОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 2ОГО ПОРЯДКА С ПОТОСЯННЫМ КОЭФФИЦИЕНТОМ

y”=py’+q=0 (56)

где p=const, q=const

y=e^rx, y’=re^rx, y”=r²e^rx

тогда подставим это решение в (56), получаем характеристическое уравнение:

r²+pr+q=0 (57)

корни этого уравнения

r_1,2=-p/2±

1. пусть р²/4-g>0, тогда r₁=-p/2+ , r₂=-p/2- , т.е. будем иметь 2линейно независимых частных решения

у₁= , y₂=

т.е. общее решение уравнения (56) будет иметь вид:

y=c₁ +c₂ (58)

2. пусть p²/2-g≠0, тогда r₁=r₂=-p/2. Будем иметь одно частное решение y₁=e^-p/2*x. Второе частное решение надо найти. Докажем, что второе частное решение имеет вид: , тогда ,

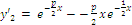подставим y₂, y’₂, y”₂ в (56). Получаем тождество:

(т.к. q= ) т.е. действительны у₂ – второе частное решение. Следовательно, в этом случае решение имеет вид:

(59)

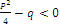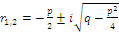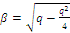3. пусть , тогда . Обозначим α=-p/2, , т.е.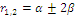

покажем, что в этом случае одно из частных решений имеет вид: y=e^2x . Подставляя это значение у и значение у₁’ и у”₁ в дифференциальное уравнение (50), получаем тождество:

действительно, у₁’=

подставим в (50) Действительно, у₁= частное решение (56). Аналогично доказывается, что 2-е частное решение = у₂= . Следовательно, общее решение (56): y= .