Глава 5

ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

БИЛЕТ 1

ОСНОВНЫЕ ПОНЯТИЯ О ФУНКЦИЯХ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Функции могут зависеть не от одной независимой переменной, от нескольких переменных. В простейшем случае эта функция , где независимые переменные х и у. Каждой упорядоченной паре значений <x;y> на плоскости XоY соответствует точка М с координатами <x;y> (М(x;y)) и тогда в каждой этой точке области определения функции D соответствует значение этой функции f(x;y) f(M).

Имеются функции 3х независимых переменных x, y, z, т.е. U=f(x;y;z), тогда область определения этой функции D – это некоторая область трехмерного пространства или же все трехмерное пространство.

В каждой точке M(x;y;z), принадлежащей этой области D, можно вычислить значение функции f(x;y;z) f(U)

Т.е. в общем случае мы имеем функцию

U=f(

Это функция n-независимых переменных а точка – точка n-мерного пространства

Область D – это некоторая область n-мерного пространства или все n-мерное пространство

Понятие предела функции обобщается на случаи любого числа независимых аргументов

Сформулируем определение предела функции 2-х независимых переменных

О1

Пусть функция определена и непрерывна в некоторой области D или во всем двухмерном пространстве , тогда пределом этой функции, при условии, что точка M(x;y) стремится к точке (т.е. называется такое постоянное число А, что выполняется условие: при любом положительном числе найдется такое положительное число , что из условий:|x- и следует неравенство . Это записывается в виде

или

Отметим, что при стремлении точки М к точке координаты этой точки х и у должны меняться таким образом, чтобы точка М (х;у) не выходила за пределы области определения D, а предельная точка должна находиться либо внутри области определения D, либо на ее границе | | | | | |

| | График функции 2-х переменных – поверхность 3-хмерного пространства над или под областью D (в зависимости от того – положительно или отрицательно значение этой функции).

Обобщим понятие предела функции на случай функции любого числа переменных

О1

Пусть функция определена и непрерывна в некоторой области или в n-мерном пространстве , тогда пределом этой функции при условии, что точка М( стремится к точке (т.е. , где k=1,2,3…n) называется такое постоянное число А, что выполняется условие: при любом положительном числе найдется такое положительное число , что из условий

Это записывается в виде или

Значения функции U=f( откладывается по (n+1) коорд. U, т.е. график этой функции представляет собой n-мерную гиперповерхность в n-мерном пространстве

БИЛЕТ 2

ЧАСТНЫЕ ПРОИЗВОДНЫЕ И ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ПЕРВОГО ПОРЯДКА

#2

ЧАСТНЫЕ ПРОИЗВОДНЫЕ И ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

О4

Если функция изменяется так, что приращение получает только одна из независимых переменных, т.е. , а остальные независимые переменные остаются постоянными, то разность между последующим значением функции и ее предшествующим значением называется ЧАСТНЫМ ПРИРАЩЕНИЕМ, соответствующим аргументу

(4)

В случае n=2 функция двух независимых переменных х и у имеет два частных приращения

(формулы 4’)

О5

Если при изменении функции меняются одновременно все независимые переменные, то разность между последующими значениями функции и ее предшествующим значением называется ПОЛНЫМ ПРИРАЩЕНИЕМ ФУНКЦИИ, т.е.

(5)

При n=2

(5’)

О6

Предел отношения частного приращения функции к приращению соответствующей независимой переменной , при условии, что приращение стремится к 0, называется ЧАСТНОЙ ПРОИЗВОДНОЙ функции по соответствующей независимой переменной

(6)

Согласно О6 функция n независимых переменных имеет n частных производных. В частности функция 2-х независимых переменных U=f(x;y) имеет 2 частных производных по х и по у.

(6’)

О7

Произведение частных производных функции по меняющейся независимой переменной на дифференциал этой переменной называется ЧАСТНЫМ ДИФФЕРЕНЦИАЛОМ функции, а сумма всех частных дифференциалов этой функции называется полным дифференциалом функции.

-­полный дифференциал

Согласно О7

(7)

Для функции 2-х переменных дифференциал функции равен

(7’)

Найдем соотношение между полным приращением функции и ее частичными производными. Для простоты будем рассматривать функцию 2-х переменных.

Тогда полное приращение равно

Применяя к этим скобкам формулу Лагранжа, получаем, что

Будем считать, что частные производные непрерывны, тогда

Переменная величина, как известно, может быть представлена в виде суммы ее предела и б.м. величины, поэтому

, где - б.м. величина

, где - б.м. величина

Подставим эти выражения в формулу для и обозначим

, а также учтем, что согласно определению дифференциала аргумента, тогда получим, что

(8)

Но, согласно формуле (5)

, где б.м. (9)

Полное приращение функции отличается от ее полного дифференциала на б.м. величину

Таким образом, полное приращение и полный дифференциал можно считать приблизительно равными, т.е.

Это соотношение используется при обработке результатов экспериментов. #3

ЧАСТНЫЕ ПРИЗВОДНЫЕ И ПОЛНЫЙ ДИФФЕРЕНЦИАЛ 1-ОГО ПОРЯДКА

Для простоты рассмотрим функцию 2-х переменных

. Эта функция имеет 2 части производных 1-го порядка, т.е.

;

Дифференцируя эти части производной по х и по у получаем части производной 2-го порядка.

При дальнейшем дифференцировании получаем частную производную 3-го порядка, а затем и частные производные более высоких порядков.

Это обобщается и на случай функций произвольного числа аргументов.

БИЛЕТ 3

ЧАСТНЫЕ ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ

#3

ЧАСТНЫЕ ПРИЗВОДНЫЕ И ПОЛНЫЙ ДИФФЕРЕНЦИАЛ 1-ОГО ПОРЯДКА

Для простоты рассмотрим функцию 2-х переменных

. Эта функция имеет 2 части производных 1-го порядка, т.е.

;

Дифференцируя эти части производной по х и по у получаем части производной 2-го порядка.

При дальнейшем дифференцировании получаем частную производную 3-го порядка, а затем и частные производные более высоких порядков.

Это обобщается и на случай функций произвольного числа аргументов.

О8

Частные производные функции нескольких переменных по различным переменным называются СМЕШАННЫМИ ПРОИЗВОДНЫМИ.

Например, СМЕШАННЫМИ ПРОИЗВОДНЫМИ называются производные 2-го порядка

,

отличающийся друг от друга порядком дифференцирования

Т1

Смешанные производные одного и того же порядка, отличающиеся только порядком дифференцирования по различным переменным, равны друг другу.

Пример

БИЛЕТ 4

ПОЛНЫЕ ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ

Рассмотрим дифференциалы высших порядков

Полный дифференциал 1-го порядка функции 2-х переменных равен

Дифференциал дифференциала 1-го порядка – это дифференциал 2-го порядка, т.е.

Дифференциал 3-го порядка – это дифференциал дифференциала 2-го порядка

Вычислим дифференциал 2-го порядка и исследуем его структуру

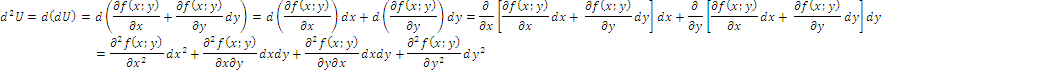
По теореме 1 смешанные производные равны, поэтому

Напишем эту формулу в символической форме

Это выражение легко обобщается на дифференциалы любого порядка, т.е. дифференциал n-го порядка от функции у

Аналогично выводятся формулы высших порядков для функции любого числа переменных

БИЛЕТ 5

#4

ПРОИЗВОДНЫЕ СЛОЖНЫХ ФУНКЦИЙ

Пусть функция зависит от 2-х промежуточных аргументов х и у, которые, в свою очередь, завися от основного аргумента t:

Получаем сложную функцию

f(

найдем ее производную по t, считая, что функции непрерывны

В #2 получаем формулу для полного приращения функции f(x;y):

где , . Разделим это равенство на

Пусть ,тогда по непрерывность функции будем иметь:

Но по определению производной

Вычисляя предел от левой и правой частей формулы (13) при получаем

₍₁₄₎

Эту формулу можно записать так же в виде:

Пусть функции зависят от 2-х аргументов U и W, тогда формула (14) обобщается на случай частных производных :

15)

БИЛЕТ 6

#5

ПРОИЗВОДНАЯ НЕЯВНОЙ ФУНКЦИИ

О3

Функция называется неявной, если функциональная зависимость переменной у от х задана неявно, т.е. в виде уравнения f(x;y)=0 нерешенного относительно у.

Найдем производную неявной функции, используя формулу (14’)

Положим, что

, следовательно

Приравняем x=t, тогда

, следовательно по формуле (14’)

т.е. производная неявной функции равна

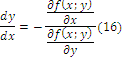
Если уравнение дает неявную функцию 2-х переменных. Тогда вместо формулы (16) получаем

(17)

(17)

БИЛЕТ 7

РЯДЫ ТЭЙЛОРА И МАКЛОРЕНА ДЛЯ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

#6

РАЗЛОЖЕНИЕ ФУНКЦИИ 1 ПЕРЕМЕННОЙ В РЯД ТЭЙЛОРА

представим в виде разложения по степеням x-a, где а- const.

Входящую в это выражение постоянную нам нужной найти, для этого нужно последовательно дифференцировать эту функцию

n-факториал

1!=1

2!=1*2=2

3!=1*2*3=6

0!=1

Формула (18) – разложение функции y=f(x) в ряд Тэйлора

(18’)

Если a=0, то

(19)

Ряд 19 – ряд Маклорена (частичный случай ряда Тэйлора)

Представим формулу (18) в другом виде, а именно через формулы различных порядков

- приращение функции

’

(20)

Формула (20) дает соотношение между приращением функции и ее дифференциалами различных порядков

БИЛЕТ 8

ФОРМУЛА РАЗЛОЖЕНИЯ В РЯД ТЭЙЛОРА ДЛЯ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

#7

РАЗЛОЖЕНИЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ В РЯД ТЭЙЛОРА

-точка в n-мерном пространстве

Тогда значение функции получается полным приращением, а каждая из координат своим приращением

Тогда формулу (20) можно обобщить на случай функции любого числа переменных и записать в виде

(21)

Рассмотрим простейший случай, функцию 2-х переменных

,тогда

, тогда

(22)

Если приращение аргументов малы, то их высшими степенями можно пренебречь. В формуле (22) ограничиться двумя первыми слагаемыми, а сумму оставить остальных слагаемых обозначить через бесконечно малую величину

Дифференциалы можно выразить через частные производные, т.е.

(23)

Перейдем в этой формуле от Декартовых к полярным

| | | | | | |

-прямоугольник

-гипотенузы

- катеты

т.е.

БИЛЕТ9

#8

ИССЛЕДОВАНИЕ ЭКСТРЕМУМОВ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ(ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМОВ)

Найдем достаточные условия экстремумов функции двух переменных

Частная производная вычисляется при т.е. в этом случае функция считается функцией одной переменной х, а необходимое условие экстремума этой функции – равенство нулю ее производной, т.е.

Аналогично при вычислении частной производной по у считается, что , в этом случае – это функция одной переменной y

(26)

Решая систему уравнений (26) и (27), получим, что

подозрительная на экстремум

В дальнейшем будем предполагать, что функция f(x;y) имеет непрерывную частную производную в этой точке и в некоторой ее окружности.

Согласно определению экстремума в точке имеет место max, если f( при любых и , т.е.

В этой точке имеет место min, если f( при любых и , т.е.

(28)

Обозначим , ,

, где

Согласно формулам (27) и (28), если при всех достаточно малых значениях z , то - точка максимума, то точка минимума

Входящий в формулу (29) квадратный трехчлен отличается от при умножении на на бесконечно малую величину, поэтому знак этого трехчлена совпадает со знаком . Таким образом, если этот трехчлен отрицательный, то в точке имеет место max, а если он положителен, то в точке имеет место min. Если квадрат трехчлена при различных значениях сохраняет свой знак, но при некоторых значениях обращается в 0, то при этом значении , а знак бесконечно малой величины нам неизвестен.

Поэтому этот случай является сомнительным, т.е. мы не можем сказать, имеется ли в точке max или min или нет. Если же квадрат трехчлена при различных значениях меняет свой знак, то условия (27) и (28) не выполняется, т.е. в т экстремума нет

| | | | | | |

| | | | | | |

| | | | | | |

Рассмотрим 3 таких значения постоянных A,B и C, при некоторых имеет место тот или иной случай

1)Пусть А , AC- , тогда квадратный трехчлен можно представить в виде A =

Числитель является суммой 2-х положительных слагаемых, которые не обращаются в 0 одновременно. Знак этого выражения совпадает со знаком знаменателя А, следовательно, если A<0, то квадратный трехчлен отрицателен и имеет место max, если A>0, то квадратный трехчлен положителен и имеет место min

2)Пусть , , тогда если , то следовательно трехчлен равен , т.е. его знак совпадает со знаком А

трехчлен равен , но , ,т.е. трехчлен имеет знак, противоположный знаку А.

Таким образом, в этом случае, при изменении трехчлен меняет свой знак т.е. в этом случае экстремум отсутствует.

3) , тогда трехчлен имеет вид , он сохраняет свой знак, совпадающий со знаком постоянной А. Например , т.е. когда трехчлен выражается в 0. Следовательно, это сомнительный случай.

4)Пусть А=0, , тогда

(

Когда мало, то , но при т.е. квадратный трехчлен меняет свой знак с изменением . Это обозначает, что экстремум отсутствует.

5)Пусть А=0, В=0, ,тогда квадратный трехчлен равен . При , т.е. это сомнительный случай.

Таким образом:

Результат исследования функции двух переменных на экстремумы представляется в виде следующей функции

А-В2	+		-	0
А	+	-	Любое А	Люб А
вывод	min	max	Нет ни min, ни max	Сомнительный случай

БИЛЕТ 10

#8

ИССЛЕДОВАНИЕ ЭКСТРЕМУМОВ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ (НЕОБХОДИМЫЕ УСЛОВИЯ ЭКСТРЕМУМОВ)

Найдем достаточные условия экстремумов функции двух переменных

Частная производная вычисляется при т.е. в этом случае функция считается функцией одной переменной х, а необходимое условие экстремума этой функции – равенство нулю ее производной, т.е.

Аналогично при вычислении частной производной по у считается, что , в этом случае – это функция одной переменной y

(26)

Решая систему уравнений (26) и (27), получим, что

подозрительная на экстремум

В дальнейшем будем предполагать, что функция f(x;y) имеет непрерывную частную производную в этой точке и в некоторой ее окружности.

Согласно определению экстремума в точке имеет место max, если f( при любых и , т.е.

В этой точке имеет место min, если f( при любых и , т.е.

(28)

Обозначим , ,

, где

Согласно формулам (27) и (28), если при всех достаточно малых значениях z , то - точка максимума, то точка минимума

Входящий в формулу (29) квадратный трехчлен отличается от при умножении на на бесконечно малую величину, поэтому знак этого трехчлена совпадает со знаком . Таким образом, если этот трехчлен отрицательный, то в точке имеет место max, а если он положителен, то в точке имеет место min. Если квадрат трехчлена при различных значениях сохраняет свой знак, но при некоторых значениях обращается в 0, то при этом значении , а знак бесконечно малой величины нам неизвестен.

Поэтому этот случай является сомнительным, т.е. мы не можем сказать, имеется ли в точке max или min или нет. Если же квадрат трехчлена при различных значениях меняет свой знак, то условия (27) и (28) не выполняется, т.е. в т экстремума нет

| | | | | | |

| | | | | | |

| | | | | | |

Рассмотрим 3 таких значения постоянных A,B и C, при некоторых имеет место тот или иной случай

1)Пусть А , AC- , тогда квадратный трехчлен можно представить в виде A =

Числитель является суммой 2-х положительных слагаемых, которые не обращаются в 0 одновременно. Знак этого выражения совпадает со знаком знаменателя А, следовательно, если A<0, то квадратный трехчлен отрицателен и имеет место max, если A>0, то квадратный трехчлен положителен и имеет место min

2)Пусть , , тогда если , то следовательно трехчлен равен , т.е. его знак совпадает со знаком А

трехчлен равен , но , ,т.е. трехчлен имеет знак, противоположный знаку А.

Таким образом, в этом случае, при изменении трехчлен меняет свой знак т.е. в этом случае экстремум отсутствует.

3) , тогда трехчлен имеет вид , он сохраняет свой знак, совпадающий со знаком постоянной А. Например , т.е. когда трехчлен выражается в 0. Следовательно, это сомнительный случай.

4)Пусть А=0, , тогда

(

Когда мало, то , но при т.е. квадратный трехчлен меняет свой знак с изменением . Это обозначает, что экстремум отсутствует.

5)Пусть А=0, В=0, ,тогда квадратный трехчлен равен . При , т.е. это сомнительный случай.

Таким образом:

Результат исследования функции двух переменных на экстремумы представляется в виде следующей функции

А-В2	+		-	0
А	+	-	Любое А	Люб А
вывод	min	max	Нет ни min, ни max	Сомнительный случай

БИЛЕТ 11

#9

ОТНОСИТЕЛЬНЫЙ ЭКСТРЕМУМ

О10

Если аргументы функции нескольких переменных независимы друг от друга, то экстремум такой функции называется АБСОЛЮТНЫМ, а если аргументы этой функции связаны некоторыми соотношениями, то экстремум такой функции называется ОТНОСИТЕЛЬНЫМ или УСЛОВНЫМ.

Рассмотрим функцию

m+n переменных

Пусть переменные связаны n-соотношениями

,где k=1,2,3,…,n

В дальнейшем для простоты записи мы не будем писать аргументы у функций

Можно считать, что первые m аргументов не зависят друг от друга, а последние аргументы зависят от 1-ых и эта зависимость выражена n-условиями (30).

Рассмотрим способ нахождения относительно экстремумов функции нескольких переменных, называемый СПОСОБОМ МНОЖИТЕЛЕЙ ЛАГРАНЖА

в такой точке формулы аргумент достигает относительного экстремума. Предполагая существование конечных частных производных в этой точке, получаем, что в этой точке частная производная 1-го порядка обращается в 0, следовательно, и ее полный дифференциал 1-го порядка тоже равен 0, т.е.

(31)

С другой стороны

Функция согласно формуле (30) равна 0, т.е. равна постоянной величине(const).

Умножим формулу (32) на множители и сложим их друг с другом и с формулой (31)

Получим

(33)

Множители называются МНОЖИТЕЛЯМИ ЛАГРАНЖА. Определим их из условия, что коэффициенты при дифференциалах аргументов , связанных друг с другом n соотношением (31), равны 0, т.е.

(34) при

Учитывая соотношения (34), получаем, что в формуле (33) остаются только члены, содержащие дифференциалы называемых переменных, т.е. получаем

(35)

Но дифференциалы независимых переменных – это произвольные их приращения. Поэтому, каждый из дифференциалов в формуле (35), кроме одного из них, можно положить равным 0. Тогда полагая S=1,2,…,m получим из формулы (35) m соотношения:

(36)

Объединяя формулы (34) и (360, получаем, что соотношение (37) справедливо при всех значениях индекса S=1,2,3,…,m+n

Таким образом, соотношения (30) и (37), в которых координаты точки заменены координатами точки , подозр. на экстремумы дают необходимое условие экстремума.

Введем вспомогательную функцию , тогда , т.е. соотношения (37) дают условия

, (S=1,2,…,m+n) (39)

К этим условиям добавляются соотношения (30)

Таким образом, нахождение относительного экстремума функции f сводится к нахождению абсолютного экстремума вспомогательной функции .