Глава 4

БИЛЕТ 1

НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ (СЛУЧАИ РАЗВРЫВНЫХ ФУНКЦИЙ)

# 8

Несобственные интегралы

Опр 5

Несобственными интегралами называются определенные интегралы от разрывных функций или определенные интегралы, взятые по бесконечным промежуткам интегрирования.

Рассмотрим 1 случай, т.е. интегралы от разрывных функций

Пусть функция y=f(x) определена на кусочном непрерывном промежутке [a;b], т.е. функция имеет конечное число разрывов 1-го рода.

В этом случае промежуток [a;b] можно разбить на конечное число таких промежутков, в которых ф-я непрерывна, а несобственный интеграл тогда будет суммой обычных определенных интегралов, взятых по промежутку непрерывности ф-и.

|

| | | | | = + + + + (39)

Это следует из геометрического смысла определения интеграла

S_ab=S_ac1 + S_c1c2 + S_c2c3 + S_c3c4 + S_c4b

Пусть функция y=f(x) определена на промежутке [a;b], причем в точке cє(a;b) (принадлежащей открытому промежутку) (внутри промежутка [a;b]) ф-я имеет разрыв 2-го рода, т.е. бесконечный разрыв и нужно вычислить несобственный интеграл

| | | | | Выделим точку разрыва, т.е. заключим ее в промежуток

(1) , (2)

Для того, чтобы получить интеграл нужно ε 1 и ε2 устремить к 0.

= + (40)

Если указанные пределы существуют и конечны, то несобственный интеграл называется сходящимся.

Если же эти пределы не существуют или бесконечны, то несобственный интеграл называется расходящимся.

Точка разрыва 2 рода может совпадать с концом промежутка [a;b].

| | | | | с=a

= (41)

| | | | | c=b

= (42)

В формуле 40 ε1 и ε2 могут совпадать

ε 1 – ε= ε

В этом случае эту формулу можно записать в виде

= (43)

Если этот предел существует и конечен, но несобственные интегралы расходятся (когда = ), то этот несобственный интеграл называется сходящимся в смысле главного значения, а величина предела в правой части формулы (43) называется главным значением несобственного интеграла.

Пример.

Вычислить интеграл

|

| | | |

Если вычислить этот интеграл по формуле 40 ( ), то получим, что

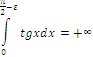
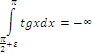
Таким образом, этот несобственный интеграл расходится.

Если же

, то по формуле 43 получаем

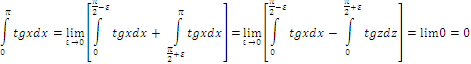
Таким образом несобственный интеграл сходится в смысле собственного значения, а его собственное значение =0.

БИЛЕТ 2

Е=НЕСОБСТВННЫЕ ИНТЕГРАЛЫ (СЛУЧАИ БЕСКОНЕЧНЫХ ПРОМЕЖУТКОВ ИНТЕГРИРОВАНИЯ)

Рассмотрим 2 случай, когда интеграл берется по промежутку. В этом случае бесконечные пределы интегрирования заменяются конечными и эти конечные пределы интегрирования устремляются в бесконечность

| | | | |

| | | | | |

| | | | | |

ПРИМЕР

f(x)=

| | | | |

Если в формуле 44, 45 и 46 пределы существуют и конечны, то несобственные интегралы являются конечными. Если же эти пределы не существуют или конечны, то несобственные интегралы являются расходящимися.

БИЛЕТ 3

ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ

#9

ПРИБЛИЖЕННЫЕ ЗНАЧЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ.

Точные вычисления определенных интегралов возможны не всегда, а иногда такие вычисления возможны, но очень трудоемки. Поэтому на практике часто используются формулы, дающие приближенные значения интегралов.

Такие формулы получаются на основании геометрического смысла определенного интеграла как площади геометрической фигуры на плоскости.

Пусть функция определена и непрерывна на промежутке .

Так как S геометрической фигуры всегда положительна, то будем считать, что

Разобьем промежуток на n равных частей длиной

| | | | | | точки деления промежутка : , тогда фигура под графиком формулы разобьется на n полосок

Для того, чтобы вычислить приближенно заменим каждую из полосок прямоугольником с основанием и высотой, равной либо левой, либо правой ординате.

Когда высоты прямоугольников равны левым ординатам, то сумма их площадей будет равна

Примем в качестве высот правую ординату, тогда

Выведем более точную приближенную формулу для вычисления определенных интегралов -> ф.трапеции

Разобьем фигуру под графиком функции на n полосок, каждая из которых имеет ширину

Каждую из этих полосок приближенно заменим трапецией с основанием, равным ординатам, и с высотой, равной

| | | | | |

| | | | | | как известно, площадь трапеции равна произведению полусуммы оснований на высоту

Суммируем площади всех трапеций, получаем приближенное выражение площади фигуры под графиком функции, т.е.

Таким образом ФОРМУЛА ТРАПЕЦИИ имеет вид

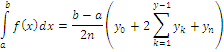
Формулы прямоугольника и трапеции являются простыми для вычисления, но их точность недостаточна. Поэтому на практике для вычисления определенных интегралов используется ФОРМУЛА СИМОНСА.

Она достаточно проста для вычисления, но имеет большую точность, чем предыдущая формула

Напишем идею вывода этой формулы

Как и раньше фигуру под графиком формулы разобьем на части одной и той же ширины

Каждую из этих частей разобьем пополам промежуточными точками и вычислим ординаты

Рассмотрим каждую полоску

| | | | | | через 3 точки, являющиеся концами ординат, в каждой из полосок проведем отрезок параболы

| | | | | |

Приближенно заменяем площадь каждой полоски площадью фигуры под параболой и суммируем все эти площади.

Получаем формулу Симпсона

Имеются другие более точные формулы для вычисления определенных интегралов, но они сложны в вычислении.