20. Линейные уравнения второго порядка

Это уравнение - неоднородное линейное; если F(x)=0, то уравнение называется однородным линейным.

Общее решение неоднородного уравнения равно сумме общего решения однородного уравнения и какого-либо частного решения неоднородного уравнения. Общее решение однородного уравнения имеет вид y=C₁y₁+C₂y₂, где C₁,C₂ - постоянные; y₁, у₂ - линейно независимые решения уравнения (две функции называются линейно независимыми, если их отношение не является постоянной). Такие решения у₁ и y₂ образуют так называемую фундаментальную систему решений.

Если известно только одно частное решение однородного уравнения у₁ то другое находится по формуле

где С - постоянная.

Если коэффициенты р(х), q(x) и F(x) разлагаются в сходящиеся ряды по степеням х-х₀ в некоторой окрестности точки х₀, то решения ищут также в форме рядов по степеням х-х₀, сходящихся в той же окрестности. Коэффициенты разложения находятся приравниванием коэффициентов при одинаковых степенях разности x-x₀.

Задача отыскания решений однородного уравнения значительно упрощается, если коэффициенты дифференциального уравнения постоянны:

где а₀, a₁, а₂ - данные числа. Решения уравнения зависят от корней характеристического уравнения a₀k²+а₁k+a₂=0. в табл. 1 даны результаты в зависимости от дискриминанта

Таблица 1.

В табл. 1 функция φ(х) есть частное решение неоднородного уравнения; оно может быть найдено по способу неопределенных коэффициентов, если правая часть дифференциального уравнения имеет следующую структуру:

где Р₁(х) и Р₂(х) - многочлены.

В общем же случае применяют вариацию произвольных постоянных, а именно: заменяют постоянные C₁ и С₂ функциями C₁(x) и С₂(х); производные этих функций должны удовлетворять системе алгебраических линейных уравнений:

Найдя С′₁ и С′₂, получают

где D₁ и D₂ - произвольные постоянные.

Уравнение вида x²y"+xp(x)y'+q(x)y=0 в том случае, если р(х) и q(x) разлагается в сходящиеся ряды по степеням х, имеет решение

где k определяется из уравнения

а коэффициенты а₀, а₁, ... находят методом неопределенных коэффициентов.

ПРИМЕР 1. Уравнение Эйлера:

В этом случае

и решение имеет вид

ПРИМЕР 2. Уравнение Бесселя:

Для k получается

откуда k=±y.

Два решения имеют вид

21. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Общее решение линейного однородного дифференциального уравнения   с непрерывными на интервале интегрирования Xкоэффициентами   определяется линейной комбинацией  , где   - линейно независимые частные решения ЛОДУ на X, а   - произвольные постоянные. Таким образом, общее решение линейного однородного дифференциального уравнения второго порядка  с постоянными коэффициентами имеет вид y₀ = C₁ ⋅ y₁ + C₂ ⋅ y₂ , где y₁ и y₂ – частные линейно независимые решения, а С₁ и C₂ – произвольные постоянные. Осталось научиться находить частные решения y₁ и y₂. Эйлер предложил искать частные решения в виде  . Если принять   частным решением уравнения  , то при подстановке этого решения в уравнение мы должны получить тождество.   Так мы получили характеристическое уравнение. Решения k₁ и k₂ этого квадратного уравнения определяют частные решения   и   нашего ЛОДУ второго порядка с постоянными коэффициентами. В зависимости от коэффициентов p и q корни характеристического уравнения могут быть:

1. действительными и различными  ,

2. действительными и совпадающими  ,

3. комплексно сопряженной парой  .

В первом случае линейно независимыми частными решениями исходного дифференциального уравнения являются   и  , общее решение ЛОДУ второго порядка с постоянными коэффициентами есть  . Функции   и   действительно линейно независимы, так как определитель Вронского   отличен от нуля для любых действительных x при  . Во втором случае одним частным решением является функция  . В качестве второго частного решения берется  . Покажем, что   действительно является частным решением ЛОДУ второго порядка с постоянными коэффициентами   и докажем линейную независимость y₁ и y₂. Так как k₁ = k₀ и k₂ = k₀ совпадающие корни характеристического уравнения, то оно имеет вид  . Следовательно,   - исходное линейное однородное дифференциальное уравнение. Подставим в него   и убедимся, что уравнение обращается в тождество:   Таким образом,   является частным решением исходного уравнения. Покажем линейную независимость функций   и  . Для этого вычислим определитель Вронского и убедимся, что он отличен от нуля. 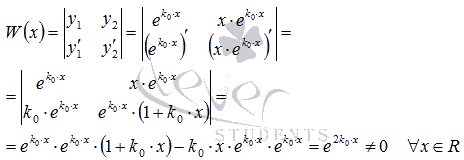  Вывод: линейно независимыми частными решениями ЛОДУ второго порядка с постоянными коэффициентами   являются   и  , и общее решение есть   при  .  В третьем случае имеем пару комплексных частных решений ЛОДУ   и  . Общее решение запишется как  . Эти частные решения могут быть заменены двумя действительными функциями   и  , соответствующими действительной и мнимой частям. Это хорошо видно, если преобразовать общее решение  , воспользовавшись формулами из теории функции комплексного переменного  :   где С₃ и С₄ – произвольные постоянные. Итак, обобщим теорию. Алгоритм нахождения общего решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами  .

1. Записываем характеристическое уравнение k² + p ⋅ k + q = 0.

2. Находим корни характеристического уравнения k₁ и k₂.

3. В зависимости от значений корней характеристического уравнения записываем общее решение ЛОДУ с постоянными коэффициентами в виде

   • , если  ;

• , если  ;

• , если  .

Рассмотрим примеры для каждого случая.  Пример. Найдите общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами  . Решение. Запишем характеристическое уравнение k² + 4 ⋅ k + 4 = 0. Найдем его корни    Получили два совпадающих корня, следовательно, общее решение имеет вид  . Пример. Найти общее решение дифференциального уравнения  . Решение. Мы имеем ЛОДУ второго порядка с постоянными коэффициентами. Запишем характеристическое уравнение и найдем его корни:   Корни действительные и различные, поэтому, общее решение однородного уравнения имеет вид  . Пример. Найти общее решение дифференциального уравнения  . Решение. Характеристическое уравнение ЛОДУ второго порядка с постоянными коэффициентами имеет вид k² - k + 3 = 0. Найдем его корни:   Получили пару комплексно сопряженных корней характеристического уравнения, следовательно, общее решение исходного уравнения имеет вид