17. Линейное дифференциальное уравнение первого порядка

В математике линейное дифференциальное уравнение имеет вид

где дифференциальный оператор L линеен, y — неизвестная функция  , а правая часть   — функция от той же переменной, что и y.

Линейный оператор L можно рассматривать в форме

Линейное дифференциальное уравнение порядка n с переменными коэффициентами имеет общий вид

Пример

Уравнение Коши — Эйлера, используемое в инженерии, является простым примером линейного дифференциального уравнения с переменными коэффициентами

Уравнение первго порядка

Линейное дифференциальное уравнение первого порядка с переменными коэффициентами имеет общий вид

Уравнения в такой форме могут быть решены путём умножения на интегрирующий множитель

получим

используем правило дифференцирования произведения

что, после интегрирования обеих частей, дает нам

Таким образом, решение линейного дифференциального уравнения первого порядка

(в частности, с постоянными коэффициентами) имеет вид

где   является константой интегрирования.

18. Понижение порядка дифференциального уравненияI. Пусть левая часть уравнения (1) не содержит явно искомую

Во многих случаях удается свести дифференциальное уравнение  -го порядка

                                                          (1)

к дифференциальному уравнению более низкого порядка, путем введения новой неизвестной функции. Рассмотрим некоторые типы уравнений, допускающих понижение порядка.

функцию  , т. е. уравнение имеет вид

.                                                     (2)

Введем новую функцию  , тогда   и уравнение (2) перепишется так:

,                                                              (3)

т. е. относительно функции   оно представляет собой уравнение  -го порядка.

Любое решение  , этого уравнения мы должны подставить в дифференциальное уравнение   и решить последнее относительно  :

.

Появилась произвольная постоянная. Часто некоторые решения дифференциального уравнения (3), не обязательно все, образуют семейство функций

,

зависящих от   параметров  . Ему соответствует семейство решений   дифференциального уравнения (2)

,

зависящих от   параметров  .

Пример 1.  .

Здесь функция   явно не входит в уравнение. Полагая  , находим   и наше уравнение принимает вид  . Разделяя переменные, имеем

,

т.е.

.

Но  , значит,  .

II. Пусть левая часть уравнения (1) не содержит явно независимую переменную  :

.                                                     (4)

Будем считать в этом уравнении   независимым переменным, а   - искомой функцией. Обозначим  .

Тогда

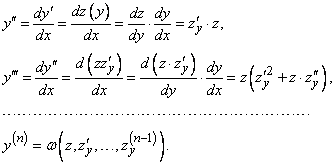
Подставляя эти значения в (4), получим дифференциальное уравнение   - го порядка относительно  . Пусть  , есть решение этого дифференциального уравнения, отличное от нуля на  . Так как  , то

.

Мы получили решение   исходного уравнения (4) в неявной форме. При этом оно зависит от произвольной постоянной  .

Но часто функции   получаются в виде семейств функций

,

зависящих от   параметров  . Им соответствующие решения   в свою очередь образуют семейство

функций, зависящих от   параметров  .

Пример 2.  .

Здесь   явно не присутствует, поэтому полагаем  . Подставляя эти значения в уравнение, имеем   или  .

Отсюда   и  .

Если  , то  .

Если  , то, разделяя переменные, получаем

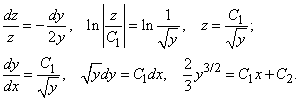
19. Линейные однородные дифференциальные уравнения 2 - го порядка

Уравнение вида 

Ly=y′′(x)+p(x)y′(x)+q(x)y(x)=f(x),   a<x<b,      (1) где p(x), q(x), f(x) - заданные на интервале (a,b) непрерывные функции, называется линейным дифференциальным уравнением 2 - го порядка. Если f(x)≡0 , то дифференциальное уравнение (1) называется однородным, в противном случае, т.е. когда f(x) тождественно не равна нулю дифференциальное уравнение (1), называется неоднородным. Рассмотрим соответствующее (1) линейное однородное дифференциальное уравнение 2 - го порядка

Ly=y′′(x)+p(x)y′(x)+q(x)y(x)=0.     (2)

Лемма~1. Если y(x) является на интервале (a,b) решением линейного однородного дифференциального уравнения (2), то произведение C·y(x), где C - произвольная постоянная, также является решением дифференциального уравнения (2).

Лемма~2. Если y1(x) и y2(x) являются решениями линейного однородного дифференциального уравнения (2) на (a,b), то и их сумма y1(x)+y2(x) также является решением дифференциального уравнения (2) на(a,b).

Следствие. Если y1(x) и y2(x) являются решениями линейного однородного дифференциального уравнения (2) на интервале (a,b), то и их линейная комбинация C1y1(x)+C2y2(x) с произвольными постоянными C1 и C2 так же является решением данного уравнения на (a,b). Теперь рассмотрим линейное однородное дифференциальное уравнение с постоянными коэффициентами 

Ly=y′′(x)+py′(x)+qy(x)=0,     (3)x∈R, 

где p и q - заданные действительные постоянные. Частное решение дифференциального уравнения (7) будем искать в виде функции

y(x)=ekx,    (4)

где k - неизвестная постоянная. Функция ekx является решением дифференциального уравнения (3) только тогда, когда k является решением алгебраического уравнения:

k2+pk+q=0,     (5)

так как Lekx=ekx(k2+pk+q). Алгебраическое уравнение (5) называется характеристическим уравнением дифференциального уравнения (3). Для характеристического уравнения возможны три случая в зависимости от знака дискриминанта D=p2−4q . 1) Пусть D=p2−4q>0 . В этом случае уравнение (5) имеет два различных действительных корня k1 и k2. Тогда функции y1(x)=ek1x и y2(x)=ek2x является на R частными решениями уравнения (3). Решения ek1x иek2x линейно независимы на R и их линейная комбинация 

y(x)=C1y1(x)+C2y2(x)=C1ek1x+C2ek2x

является общим решением дифференциального уравнения (3).

2) Пусть D=p2−4q=0 . Тогда корни уравнения (5) вещественные и совпадают k1=k2=k0.  Общее решение дифференциального уравнения (3) определяется по формуле:

y(x)=C1ek0x+C2xek0x.

 

3) Пусть D=p2−4q<0 . Тогда корни уравнения (9) являются комплексно-сопряженными числамиk1=α+iβ, k2=α−iβ , где α, β -- действительные числа, β/=0 , i2=−1 .  Общее решение дифференциального уравнения (3):

y(x)=C1eα xcosβ x+C2eα xsinβ x=

=eα x(C1cosβ x+C2sinβ x).

 

Эта теория переносится также на линейные однородные дифференциальные  уравнения n - го порядка

y(n)+a1(x)y(n−1)+...+an−1(x)y′+an(x)y=f(x),     (6)

где ai(x), i=1,n,   f(x) - заданные на интервале (a,b) функции.  Если y1(x), y2(x), ..., yn(x) образуют фундаментальную систему частных решений дифференциальных уравнения (6), то их линейная комбинация 

y(x)=C1y1(x)+C2y2(x)+...+Cnyn(x)

является общим решением дифференциального уравнения (6). В случае дифференциального уравнения (6) с постоянными коэффициентами ai характеристическое уравнение имеет вид

kn+a1kn−1+...+an−1k+an=0.