Лекция 6. Колебания с угловой и импульсной модуляцией

Радиосигналы с угловой модуляцией. Временное, спектральное и векторное представление УМК. Понятие девиации частоты и индекса модуляции. Сигналы с импульсной модуляцией.

При угловой модуляции управляющий сигнал воздействует на полную фазу несущей.

Поскольку мгновенная частота и полная фаза связаны между собой:

(t) = ,

2f (t) = , (6.1)

то возможна реализация частотной или фазовой модуляции, которые тоже взаимосвязаны.

Примечание: в дальнейшем для упрощения постоянный множитель 2 опущен.

При частотной модуляции мгновенная частота изменяется по закону модулирующего сигнала:

f (t) = f₀ + f_д s(t), (6.2)

где f_д – девиация частоты (максимальное отклонение от среднего значения).

Воспользовавшись (6.1), запишем

_чм(t) = = f₀t + f_д ,

т.е. полная фаза изменяется по закону интеграла от модулирующего сигнала.

Выражение для сигнала с ЧМ окончательно принимает вид:

u_чм(t) = U₀ cos [ f₀t + f_д +₀]. (6.3)

При модуляции чистым тоном имеем

s(t) = S_mcos F₀t,

f(t) = f₀t + f_д cos F₀t,

причем f_д = k_чмS_m , т.е. девиация частоты прямо пропорциональна амплитуде модулирующего сигнала и не зависит от его частоты F₀.

Полная фаза колебания окажется равной

_чм(t) = f₀t + (f_д/ F₀ )sin F₀t + ₀ = f₀t + msin F₀t + ₀.

Здесь параметр m = f_д/ F₀ носит название индекса частотной модуляции.

Окончательное выражение для ЧМ-сигнала при модуляции чистым тоном:

u_чм(t) = U₀ cos [ f₀t + msin F₀t + ₀]. (6.4)

При фазовой модуляции по закону управляющего сигнала изменяется полная фаза колебания:

_чм(t) = f₀t + ms(t) + ₀ . (6.5)

Основной параметр здесь индекс m – максимальное отклонение фазы от среднего значения.

С учетом сказанного выражение для ФМ приобретает следующий вид:

u_фм(t) = U₀ cos [ f₀t + ms(t) + ₀]. (6.6)

Мгновенная частота при этом меняется по закону производной от управляющего сигнала

f (t) = = f₀ + m .

При модуляции чистым тоном имеем

_чм(t) = mcos(F₀t) + ₀

m = k_фмS_m ,

т.е. индекс модуляции при ФМ прямо пропорционален амплитуде модулирующего сигнала и не зависит от его частоты F₀.

Мгновенная частота определится согласно формулам (6.1):

f (t) = = f₀ – m F₀ sin(F₀t) = f₀ – f_д sin(F₀t) ,

где f_д = m F₀ – девиация частоты при ФМ.

Окончательное выражение для ФМ-сигнала при модуляции чистым тоном:

u_чм(t) = U₀ cos [ f₀t + mcos F₀t + ₀]. (6.7)

Сравнивая (6.4) и (6.7), можно сделать вывод, что при угловой модуляции гармоническим сигналом (чистым тоном) ЧМ и ФМ оказываются неразличимы.

Сказанное иллюстрирует рис. 6.1 (слева – ЧМ, справа – ФМ).

Чтобы выяснить, с какой модуляцией мы имеем дело, следует определить, как меняется индекс и девиация частоты при изменении частоты гармонического модулирующего сигнала F₀ (рис. 6.2, слева – ЧМ, справа – ФМ). Если девиация неизменна, а индекс уменьшается обратно пропорционально росту частоты, то это частотная модуляция. Если постоянен индекс, а девиация прямо пропорциональна частоте модулирующего сигнала, то это фазовая модуляция.

Различие между ЧМ и ФМ сигналами в полной мере проявляется, когда модуляция осуществляется сигналом произвольной формы.

Пример 6.1.

Пусть исходный модулирующий сигнал имеет треугольную форму (s_у(t) на рис. 6.3 вверху). Построить временные диаграммы при частотной и фазовой модуляции.

Решение.

Воспользуемся соотношениями (6.1). Учитывая, что производная линейно-нарастающего сигнала равна постоянной, а интеграл представляет собой параболическую функцию времени (рис. 6.3, слева – ЧМ, справа – ФМ).

Сигнал с УМК можно представить в комплексной форме

u_ум(t) = = .

Здесь – медленно меняющаяся комплексная огибающая.

Векторная диаграмма УМК на комплексной плоскости изображена на рис. 6.4.

В процессе модуляции длина вектора U₀ остается неизменной, а изменяется угловое положение  (отсюда термин "угловая модуляция"). Максимальное угловое отклонение равно индексу модуляции m. Таким образом, наглядной иллюстрацией УМК на комплексной плоскости служит "качающийся" вектор.

Чтобы получить спектральное представление сигнала с угловой модуляцией, рассмотрим частный случай. Пусть модуляция осуществляется чистым тоном, причем индекс мал m << 1 (узкополосная УМ).

Перепишем выражение (6.3) так

u_ум(t) = U₀ cos [ f₀t + (t)]. (6.8)

Используя известное соотношение

cos (+) = cos  cos – sin sin, преобразуем (6.8) так

u_ум(t) = U₀ cos[(t)] cos (f₀t) – U₀ sin[(t)] sin (f₀t). (6.9)

Сомножители U₀ cos[(t)] = U_с(t) и U₀ sin[(t)] = U_s(t) в (6.9) можно рассматривать как медленно меняющуюся амплитуду некоторого гармонического колебания, имеющего частоту f₀.

Тогда УМК представляет собой сумму двух амплитудно-модулированных гармонических колебаний находящихся в квадратуре (т.е. со сдвигом фаз, равным 90).

При модуляции чистым тоном (t) = m sin F₀t (см. формулу (6.4)).

Перепишем (6.9) с учетом этого так

u_ум(t) = U₀ cos[m sin F₀t ] cos (f₀t) – U₀ sin[m sin F₀t] sin (f₀t). (6.10)

Если m << 1 , то cos[m sin F₀t ]  1, а sin[m sin F₀t]  m sin F₀t.

Тогда (6.10) запишется в виде

u_ум(t) = U₀ cos (f₀t) – U₀ m sin F₀t sin (f₀t) =

= U₀ cos (f₀t) + U₀ m /2 cos [(f₀ + F₀ )t ] – U₀ m /2 cos [(f₀ – F₀ )t ]. (6.11)

Сравнивая (6.11) и (5.4), можно сделать вывод, что в данном случае УМК представляет собой АМК, в котором НБК инвертировано.

На рис. 6.5 изображена спектральная диаграмма, соответствующая (6.11).

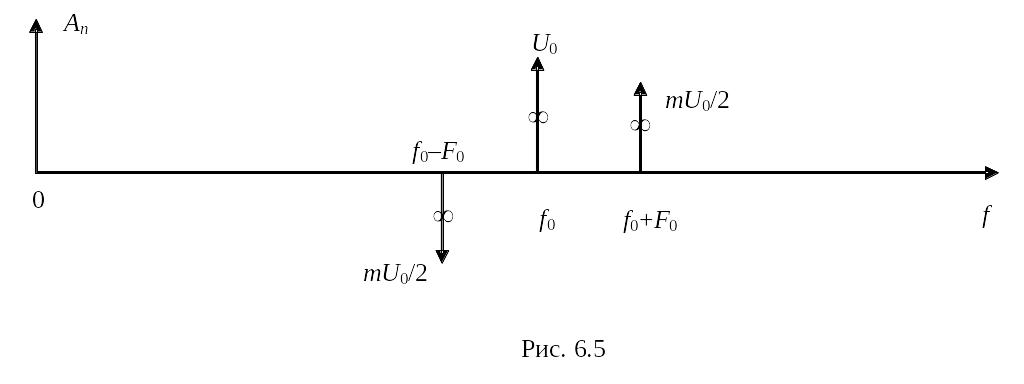
Наглядное представление об этих преобразованиях дает векторная диаграмма (рис. 6.6).

Пунктиром на векторной диаграмме обозначено положение вектора НБК при АМ. При УМ этот вектор поворачивается на угол 180 против часовой стрелки. Длина векторов боковых колебаний одинакова и равна mU₀/2.

Результирующие векторы в разные моменты времени показаны штрихпунктирной линией. Их максимальное отклонение от исходного положения равно m.

Треугольник 00'А прямоугольный, поэтому U_ > U₀ , т.е. в процессе угловой модуляции амплитуда не остается постоянной (наблюдается паразитная АМ), но поскольку m<<1 , этим изменением можно пренебречь (треугольник 00'А считать равнобедренным).

Таким образом, при узкополосной УМ ширина спектра равна удвоенной частоте модулирующего сигнала.

В случае широкополосной УМ переход от (6.10) к (6.11) будет более сложным. Опуская промежуточные преобразования, рассмотрим окончательный результат (рис. 6.7).

Спектральная диаграмма содержит бесконечный набор гармоник, амплитуды которых зависят от номера, U₀ и m .

Здесь J_n(m) = – функция Бесселя, значения которой табулированы.

Проанализируем рис. 6.7 и сделаем некоторые выводы.

1. Спектр дискретный, гармоники существуют на частотах кратных F₀.

2. Спектральные компоненты в области с частотами меньшими f₀ знакопеременные.

3. С ростом номера амплитуда гармоник быстро уменьшается.

4. Теоретически спектр бесконечен, поэтому на практике его приходится ограничивать.

5. При n > m+1 J_n(m) < 0,01, поэтому практическая ширина спектра широкополосного УМК равна 2(m+1) F₀, что существенно превышает ширину спектра узкополосного УМК и АМК (2F₀).

Общий вывод – при угловой модуляции произвольным сигналом порождается бесконечное число составляющих с частотами kf₀ lF₀, где k и l = {0, 1, 2 ...}.

Рассмотрим влияние амплитуды и частоты модулирующего сигнала на спектр ЧМК и ФМК (табл. 6.1).

Таблица 6.1