Лекция 7. Линейные радиотехнические цепи

Классификация радиотехнических цепей. Параметры и характеристики линейных цепей. Методы анализа линейных цепей. Прохождение радиосигналов через линейные цепи.

Классификация радиотехнических цепей (систем) приведена на рис. 7.1.

Любая цепь как система описывается совокупностью дифференциальных уравнений n-го порядка. Максимальный порядок дифференциальных уравнений, описывающих радиотехническую цепь, определяется числом независимых реактивных элементов (емкостей и индуктивностей). Так цепь на рис. 7.2, а первого порядка, а на рис. 7.2, б – второго.

Число полюсов определяется количеством независимых контуров цепи. Как правило, рассматривают многополюсники с четным числом полюсов. Самые распространенные из них – четырехполюсники, имеющие один вход и один выход (рис. 7.2). Для теоретического описания четырехполюсников разработаны системы Y-, Z-, H- и G-параметров. Пример – описание транзистора как четырехполюсника системой H-параметров:

. (7.1)

Здесь h₁₁ – входное сопротивление, h₁₂ – коэффициент обратной связи по напряжению, h₂₁ – коэффициент передачи по току, h₂₂ – выходная проводимость.

Подразделение цепей (систем) на линейные и нелинейные – одно из фундаментальных.

В теории систем рассматривают две основные задачи: анализ и синтез.

С точки зрения анализа цепь считают линейной, если она состоит только из линейных элементов (сопротивлений, емкостей, индуктивностей без сердечника, источников напряжения и тока). Для таких элементов выполняется закон Ома: линейная связь между падением напряжения на элементе и током через него. Добавление хотя бы одного нелинейного элемента (например, вентильного диода) превращает всю цепь в нелинейную.

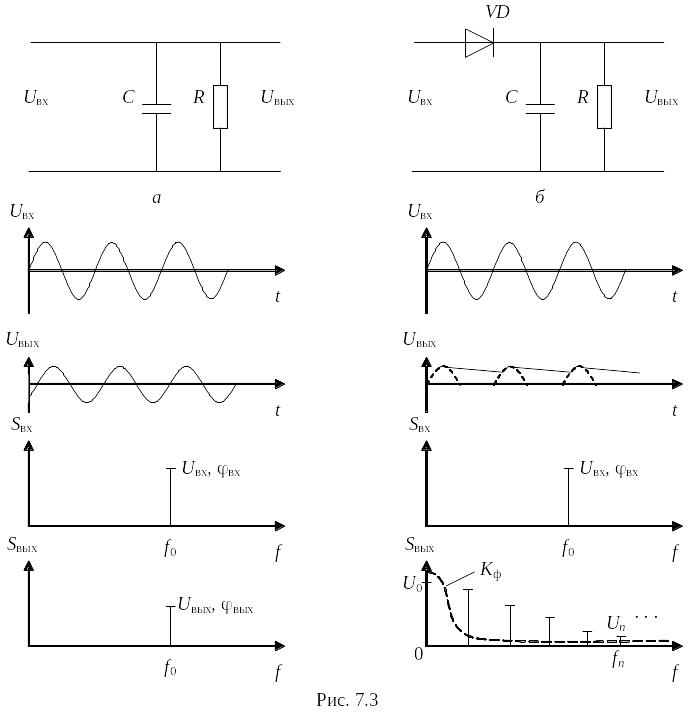
С точки зрения синтеза ставят вопрос о назначении цепи. Некоторые задачи хорошо выполняют линейные цепи, а в других случаях без нелинейных элементов не обойтись. В самом общем случае можно считать, что линейные цепи выполняют фильтрацию сигнала, т.е. пропускание одних спектральных составляющих и подавление других. В процессе фильтрации происходит обеднение спектра сигнала. Нелинейные цепи способны порождать новые спектральные составляющие, которые отсутствовали в спектре исходного сигнала. Различия между линей ной и нелинейной цепью иллюстрирует рис. 7.3.

На рис. 7.3, а изображен RC-фильтр низких частот, очевидно, что это линейная схема. При прохождении входного сигнала через такой фильтр постоянная составляющая передается без изменений, а далее с ростом частоты амплитуда гармоник уменьшается. Для определенности подадим на вход цепи синусоидальный сигнал с некоторой частотой f₀, лежащей в середине диапазона пропускания фильтра. Форма сигнала на выходе сохранится (это тоже будет гармонический процесс), изменятся только параметры: амплитуда и фаза сигнала.

Если в схему добавить полупроводниковый диод VD (рис. 7.3, б), то характер процессов существенно изменится. Предположим, что емкость С отсутствует, тогда при подаче на вход непрерывного гармонического сигнала выходной сигнал будет представлять собой прерывистую последовательность косинусоидальных импульсов, обладающую сложным спектральным составом. Добавление емкости C приведет к сглаживанию сигнала (RС-фильтр подавляет высшие частоты и на выходе получаем постоянную составляющую (которой не было в спектре входного сигнала), т.е. постоянный ток: схема работает как однополупериодный выпрямитель.

Стационарной называют такую цепь или систему, все параметры и характеристики которой остаются неизменными на интервале наблюдения, в противном случае система будет нестационарной.

В отличие от активной, пассивная цепь не содержит в своем составе источников ЭДС или тока.

Для широкополосной цепи выполняется соотношение

f/f₀ >> 1, (7.2)

где f – рабочая полоса частот, f₀ – центральная частота.

Если соотношение (7.2) не справедливо, то цепь узкополосная. Узкополосные цепи инерционны, а широкополосные – быстродействующие.

Цепь с обратной связью состоит из основного звена с коэффициентом передачи амплитуды K и фазовым сдвигом  и звена обратной связи с коэффициентом передачи амплитуды  и фазовым сдвигом  (рис. 7.4). Характер цепи с обратной связью зависит от соотношения амплитуд и фаз входного воздействия и сигнала обратной связи.

Суммарный коэффициент передачи определяется по формуле

. (7.3)

Точки в (7.3) над и означают комплексный характер этих величин, знак "плюс" соответствует отрицательной ОС, "минус" – положительной.

При ПОС знаменатель (7.3) может обращаться в ноль:

1 –  0.

Отсюда получаем так называемые условия баланса амплитуд и фаз:

(т.е. суммарное усиление в петле ОС равно единице),

(т.е. суммарный сдвиг фаз в петле ОС кратен 360).

При выполнении этих условий в системе возникают автоколебания (система становится генератором незатухающих колебаний).

При подаче импульсного сигнала на вход апериодической цепи отклик изменяется монотонно, для резонансной цепи сигнал на выходе имеет несколько локальных экстремумов.

Определить является ли цепь аналоговой или цифровой можно, выделив центральный обрабатывающий элемент (процессор). Если основная обработка сигнала осуществляется аналоговым процессором, то вся цепь аналоговая, если процессор цифровой, то цепь цифровая, независимо от наличия каких-либо вспомогательных (аналоговых или цифровых) цепей.

Элементы в цепях с сосредоточенными параметрами представляют собой отдельные конструктивы (конденсаторы, обладающие емкостью, резисторы, имеющие определенное сопротивление и т.п.). Цепи с распределенными параметрами (иначе их называют длинными линиями) характеризуются погонными величинами (на пример емкость на единицу длины), выделить емкость в виде отдельного элемента – конденсатора – в таких цепях нельзя.

Реакция безынерционной цепи на входное воздействие наступает мгновенно и независимо от предыдущего состояния. Цепи с последействием обладают "памятью": сигнал на выходе определяется не только мгновенным, но и предыдущими значениями входного сигнала. Как правило, сложную цепь при анализе разделяют на безынерционные нелинейные элементы и линейные (инерционные) каскады.

На практике часто пользуются упрощенной классификацией цепей по их назначению. Так разделяют силовые и управляющие (сигнальные) цепи, цепи постоянного и переменного тока и т.п.

Основные характеристики линейных цепей:

1. Импульсная h(t) – реакция цепи на входное воздействие в виде -функции (см. примечание к рис. 3.9).

2. Переходная g(t) – реакция цепи на входное воздействие в виде ступенчатой -функции (единичного скачка).

3. Передаточная – реакция цепи на входное воздействие в виде гармонического сигнала.

Все эти характеристики взаимосвязаны друг с другом:

h(t) = g(t);

g(t) = ; (7.4)

= F[h(t)] = .

Комплексный характер передаточной характеристики означает учет изменения не только амплитуды, но и фазы сигнала. Модуль – это амплитудно-частотная характеристика цепи (АЧХ), аргумент – фазо-частотная характеристика (ФЧХ).

Рассмотрим практически важный пример.

Пример 7.1.

Необходимо найти передаточную характеристику неискажающей цепи.

Решение.

Сигнал на выходе неискажающей цепи описывается следующим выражением:

s_вых(t) = K₀ s_вх(t – t₀),

где K₀ – постоянный масштабирующий множитель, t₀ – постоянный временной сдвиг (запаздывание сигнала).

Таким образом, сигнал на выходе представляет собой копию входного сигнала с амплитудой, измененной в K₀ раз, смещенную вправо по оси времени на величину t₀ .

Найдем спектральную плотность выходного сигнала:

= F[s_вых(t)] = F[K₀ s_вх(t – t₀)] = K₀ F[s_вх(t – t₀)].

Воспользуемся теоремой запаздывания (см. формулу (4.8)), получим:

= K₀ exp(–i2f t₀).

Произведение K₀ exp(–i2f t₀) здесь не что иное, как комплекснозначная передаточная функция неискажающей цепи:

= K₀ exp(–i2f t₀). (7.5)

Отсюда получим выражения для АЧХ и ФЧХ неискажающей цепи (рис. 7.5):

АЧХ = K₀ = const – равномерная во всем диапазоне частот входного сигнала;

ФЧХ = –2t₀ f – линейная во всем диапазоне частот.

Теперь можно определить импульсную характеристику неискажающей цепи:

Согласно (7.4) h_ни(t) = F^–1[ ] = F^–1[K₀ exp(–i2f t₀)]. Воспользовавшись теоремой двойственности (4.6), окончательно получим

h_ни(t) = K₀ (t–t₀). (7.6)

Существует два основных метода анализа цепей:

1. Временнóй – с использованием импульсной характеристики.

2. Частотный – с помощью передаточной характеристики.

В основе указанных методов лежит принцип суперпозиции (4.5), который можно сформулировать так: "результат суммы есть сумма результатов".

При временнóм методе сигнал в области времени разбивают на короткие интервалы, т.е. представляют в виде суммы коротких импульсов (рис. 7.6). Импульсная характеристика выступает в роли весовой функции. Сигнал на выходе цепи вычисляют с помощью интеграла Дюамеля:

s_вых(t) = . (7.7)

Сравнивая (7.7) и (2.6), можно сделать вывод, что отклик представляет собой свертку входного сигнала с импульсной характеристикой цепи:

s_вых(t) = s_вх(t) * h(t). (7.8)

Суть временного метода можно пояснить так: сложный входной сигнал представлен в виде совокупности элементарных воздействий – бесконечно коротких импульсов (-функций). Отклик цепи на каждую такую -функцию – это импульсная характеристика h(t). Параметр  соответствует смещению импульсной характеристики от момента начала t_н до окончания t_к входного воздействия. Далее согласно принципу суперпозиции в результате интегрирования получаем выходной отклик цепи.

Таким образом, алгоритм временнóго метода заключается в вычислении свертки (при вычислении на компьютере используют алгоритмы дискретной свертки)

Спектральный метод расчета включает три этапа.

1. Преобразование исходного сигнала во входной спектр:

s_вх(t)  .

2. Вычисление спектра на выходе цепи:

= . (7.9)

3. Преобразование выходного спектра в сигнал на выходе.

 s_вых(t) .

Таким образом, в качестве весовой функции здесь выступает передаточная характеристика цепи.

На первом этапе по формуле, аналогичной (4.3) вычисляют Фурье-образ входного сигнала.

На втором этапе находят произведение спектральной плотности и передаточной характеристики.

Третий этап заключается в обратном преобразовании Фурье по формуле, аналогичной (4.4).

Окончательно формула для расчета выходного сигнала спектральным методом получается такой

s_вых(t) = . (7.10)

При аналитическом расчете спектральным методом часто применяют преобразование Лапласа:

s_вых(t) = , (7.11)

где р = i2f.

Взаимосвязь временнóго и спектрального метода можно проиллюстрировать так. Возьмем выражение (7.8) и выполним преобразование Фурье:

F [s_вых(t) ] = F [s_вх(t) * h(t)].

По теореме о свертке (4.13) получим

= F [s_вх(t)] F [h(t)] = ,

что эквивалентно выражению (7.9).

При расчетах на компьютере используют алгоритмы дискретного и быстрого преобразования Фурье (ДПФ и БПФ).

Сравнивая вычислительную реализацию спектрального и временнóго метода, можно сделать вывод об отсутствии преимуществ одного метода перед другим. Выбор того или иного метода расчета определяется разработчиком исходя их условий конкретной практической задачи. Например, если по условию имеется спектр сигнала на входе, то целесообразнее воспользоваться спектральным методом расчета.

Рассмотрим примеры прохождения радиосигналов через линейные цепи.

Пример. 7.2. Прохождение прямоугольного импульса через идеальную и реальную дифференцирующую цепь.

Пусть на вход цепи подан одиночный прямоугольный импульс амплитудой U_m и длительностью t_и (см. рис. 2.5). Цепь осуществляет дифференцирование по времени. Определить АЧХ и ФЧХ цепи и найти сигнал на выходе.

Решение.

Сигнал на выходе идеальной дифференцирующей цепи равен

s_вых(t) = K₀ds_вх(t)/dt.

Перейдем в область частот, согласно теореме о дифференцировании (4.10) получим

= F[s_вых(t)] = i2f K₀ .

Сравнивая полученное выражение с (7.9), можно сделать вывод, что передаточная характеристика идеальной дифференцирующей цепи

= i2f K₀.

Отсюда АЧХ  = K₀ f , а ФЧХ _идц(f) = /2 (рис. 7.7).

Простейшая цепь, осуществляющая операцию дифференцирования (ФВЧ), изображена на рис. 7.8, а, а выходные сигналы, соответствующие прямоугольному импульсу, продифференцированному идеальной и реальной цепями – на рис. 7.8, б и в соответственно. Чтобы реальная цепь приближалась по свойствам к идеальной, необходимо уменьшать значение RC.

Пример 7.3. Прохождение прямоугольного импульса через идеальную и реальную интегрирующую цепь.

Пусть на вход цепи подан одиночный прямоугольный импульс амплитудой U₀ и длительностью t_и (см. рис. 2.5). Цепь осуществляет интегрирование по времени. Определить АЧХ и ФЧХ цепи и найти сигнал на выходе.

Решение.

Сигнал на выходе идеальной интегрирующей цепи равен

s_вых(t) = K₀ .

Перейдем в область частот, согласно теореме об интегрировании (4.11) получим

= F[s_вых(t)] = (1/i2f) K₀ .

Сравнивая полученное выражение с (7.9), можно сделать вывод, что передаточная характеристика идеальной интегрирующей цепи

= K₀/i2f.

Отсюда АЧХ  = K₀ /f , а ФЧХ _ииц(f) = –/2 (рис. 7.9).

Простейшая цепь, осуществляющая операцию интегрирования (ФНЧ), изображена на рис. 7.10, а, а выходные сигналы, соответствующие прямоугольному импульсу, проинтегрированному идеальной и реальной цепями – на рис. 7.10, б и в соответственно. Чтобы реальная цепь приближалась по свойствам к идеальной, необходимо увеличивать значение RC.

Пример 7.4. Прохождение АМК через избирательную цепь.

Пусть на вход цепи подан амплитудно-модулированный сигнал. Амплитуда несущей равна U₀ , частота – f₀. Модуляция осуществляется чистым тоном, частота модулирующего сигнала равна F₀ (см. рис. 5.1). Положим, что начальные фазы несущей и боковых равны нулю.

АЧХ и ФЧХ избирательной цепи описывается выражениями

K(f) = , (f) = arctg (Qf/f_ц).

Найти сигнал на выходе.

Решение.

Поскольку по условию задачи известны АЧХ и ФЧХ цепи, воспользуемся спектральным методом.

Спектр АМК при модуляции чистым тоном был получен в лекции 5 (см. рис. 5.2).

Графики АЧХ и ФЧХ избирательной цепи приведены на рис. 7.11.

Проанализируем процесс прохождения сигнала через цепь в двух случаях:

1. При f_ц = f₀ , так называемая точная настройка.

2. При расстройке f_ц  f₀ .

Совместим спектральную диаграмму АМК и графики АЧХ и ФЧХ избирательной цепи и выполним графическое перемножение.

Полученные результаты для точной настройки иллюстрирует рис. 7.12, для расстройки – рис. 7.13.

Очевидно, что при точной настройке изменяются амплитуды несущей и боковых колебаний, кроме того боковые спектральные составляющие приобретают дополнительные равные по величине и противоположные по знаку фазовые сдвиги. В целом симметрия спектральной диаграммы выходного сигнала сохраняется.

В случае расстройки изменяются амплитуды несущей и боковых, причем эти изменения различны для спектральных составляющих ВБК и НБК. Спектральные составляющие несущей НБК и ВБК приобретают различные по величине фазовые сдвиги. В результате спектральная диаграмма выходного сигнала теряет симметрию, следовательно, форма выходного сигнала искажается.