
- •Министерство образования и науки Российской Федерации Балтийский государственный технический университет «Военмех»
- •Лекция 1. Введение в радиоэлектронику
- •Этапы развития и области применения радиоэлектроники
- •Классификация радиоволн
- •Лекция 2. Сигналы и их временные модели
- •Лекция 3. Сигналы и их спектры
- •Лекция 4. Дискретизация сигнала и спектра
- •Лекция 5. Амплитудно-модулированные колебания
- •Лекция 6. Колебания с угловой и импульсной модуляцией
- •Зависимость ширины спектра чм и фм от параметров модулирующего сигнала
- •Сравнение простейших сигналов с импульсной модуляцией
- •Области применения модулированных сигналов
- •Лекция 7. Линейные радиотехнические цепи
- •Лекция 8. Нелинейные радиотехнические цепи
- •Лекция 9. Радиопередатчики
- •Лекция 10. Радиоприемники
- •Библиографический список
- •Вопросы для самоконтроля
- •Содержание
Лекция 3. Сигналы и их спектры
Основы спектрального анализа детерминированных сигналов. Спектральный анализ периодических и непериодических сигналов. Ряд Фурье. Примеры спектров простейших сигналов.
Спектральный анализ радиосигналов основан на разложении по базису ортогональных функций.
В математике понятие ортогональности функций y(x) в общем виде формулируется следующим образом:
![]() при m n
;
при m n
;
![]() при m = n .
(3.1)
при m = n .
(3.1)
Применительно к радиотехнике с физической точки зрения это означает, что некоторые два сигнала обладают ненулевой собственной энергией, но их взаимная энергия равна нулю. Таким образом, при спектральном разложении соблюдается закон сохранения энергии: энергия исходного сигнала равна совокупности энергии спектральных составляющих.
Самый распространенный в радиоэлектронике базис – базис тригонометрических функций (разложение по гармоническим сигналам).
Основные свойства гармонических сигналов, которые обусловливают их применимость:
условие ортогональности выполняется на интервале, кратном периоду;
форма гармонических сигналов сохраняется при линейных преобразованиях (изменяется только амплитуда и фаза);
возможно использование методов анализа и синтеза, разработанных в электротехнике применительно к синусоидальным колебаниям.
В случае периодического исходного сигнала при разложении в спектр получаем бесконечную сумму ряда
s(t)
= a0/2
+
![]() [ancos(2nf0t)
+ bnsin(2nf0t)],
(3.2)
[ancos(2nf0t)
+ bnsin(2nf0t)],
(3.2)
где an и bn – коэффициенты разложения (спектральные коэффициенты), n – номер гармоники, f0 – частота первой гармоники.
Выражение (3.2) известно как тригонометрический ряд Фурье. Коэффициент a0/2 называют постоянной составляющей сигнала.
На практике формула (3.2) неудобна, поскольку коэффициенты разложения an и bn не имеют подходящей физической интерпретации.
Учитывая, что любую тригонометрическую функцию можно привести к виду A0cos(2f0 + 0) приведем альтернативную запись тригонометрического ряда Фурье:
s(t) = А0/2 + [Аncos(2nf0t) + n]. (3.3)
Связь коэффициентов в формулах (3.2) и (3.3):
An
=
![]() ,
n = – arctg
(bn /an).
(3.4)
,
n = – arctg
(bn /an).
(3.4)
Физически коэффициенты An – это амплитуда, а n – фаза гармоники. Совокупность спектральных коэффициентов называют спектром сигнала в выбранном базисе.
Коэффициенты спектрального разложения вычисляют по следующим формулам:
an
=
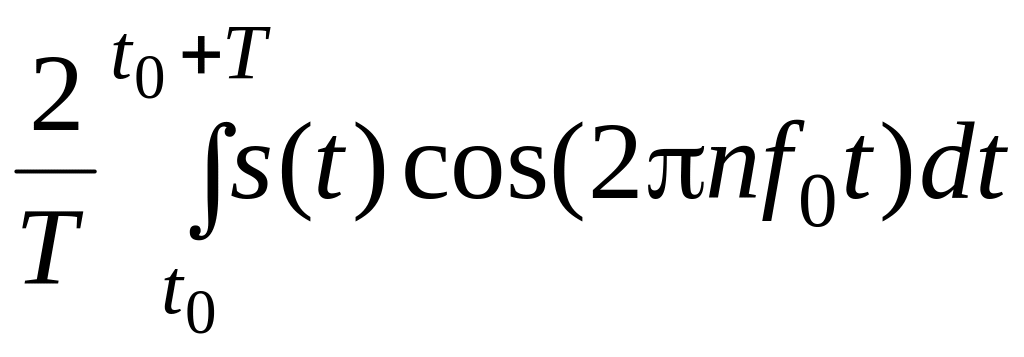 ;
;
bn
=
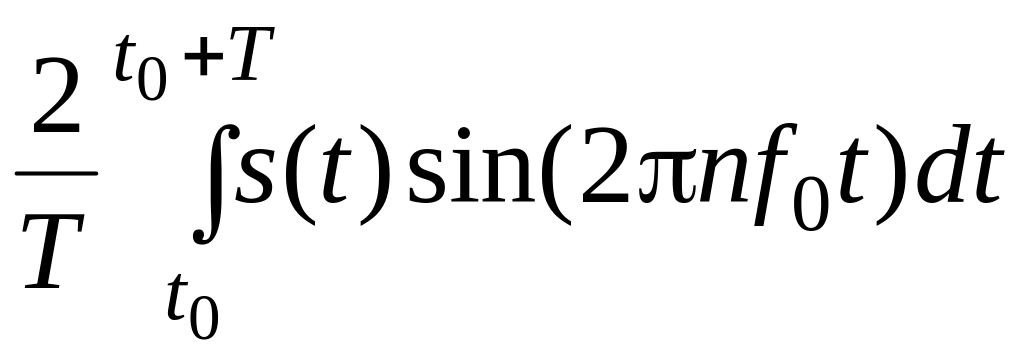 ,
(3.5)
,
(3.5)
Рассмотрим примеры разложения наиболее часто встречающихся сигналов по гармоникам.
Пример 3.1. Пусть задан исходный периодический сигнал sп(t) в виде бесконечной последовательности униполярных прямоугольных импульсов (рис. 3.1).

Воспользовавшись формулами (3.4), (3.5) и проведя несложные преобразования, получим
An
= (2Umtи/Tи)![]() ;
;
n = 0, , 2 и т.д.
Здесь использована функция sinc (x) = sin(x)/x (рис. 3.2).

Рис. 3.2
На рис. 3.3 приведено графическое представление спектра амплитуд и фаз рассмотренной последовательности прямоугольных импульсов.

Анализируя рис. 3.3, можно сделать следующие основные выводы:
1. Спектр бесконечной последовательности прямоугольных импульсов бесконечен.
2. При f = 0 имеем амплитуду постоянной составляющей A0/2.
3. Спектральные составляющие существуют только при определенных дискретных значениях частоты, кратных f0.
4. Амплитуда спектральных составляющих убывает с ростом частоты по закону функции sinc.
5. При частотах, кратных 1/tи амплитуда равна нулю.
6. Фаза принимает значения 0, .
Рассмотрим как влияет изменение длительности импульсов и периода их следования на результирующий спектр.
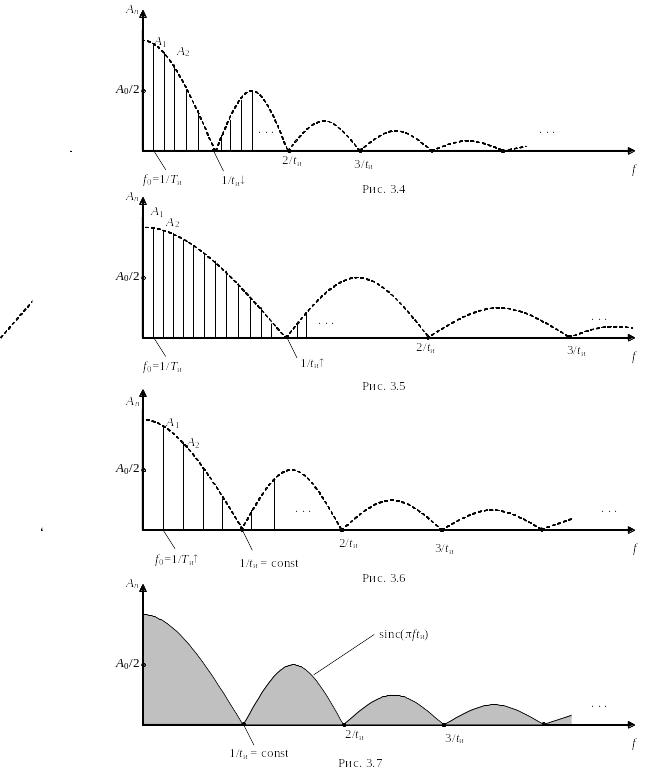
1. Пусть Tи = const, tи var. Частоты гармоник не зависят от tи и остаются постоянными. При увеличении длительности импульсов величина 1/tи уменьшается, спектр сжимается (рис. 3.4); при уменьшении длительности импульсов спектр растягивается (рис. 3.5). Для наглядности фазы n не показаны.
2. Пусть tи = const, Tи var. Очевидно, что ширина спектра не зависит от Tи и будет неизменной. Изменяется число спектральных составляющих.
Примем для определенности, что период уменьшается, тогда величина 1/Tи растет, а число гармоник уменьшается (рис. 3.6). С ростом Tи насыщенность гармониками возрастает и в пределе при Tи расстояние между соседними спектральными составляющими стремится к нулю и спектр становится сплошным (рис. 3.7). Попутно заметим, что при Tи периодическая последовательность превращается в одиночный импульс (непериодический сигнал). Непериодические сигналы и их характеристики будут подробнее рассмотрены в лекции 4.
Пример 3.2. Пусть задан сигнал в виде бесконечной синусоиды с постоянной амплитудой и нулевой начальной фазой (рис. 3.8):
s(t) = Um sin (2f0t). (3.6)

Формально сигнал вида (3.6) представить в виде разложения на элементарные математические функции невозможно, поскольку для него не выполняется условие абсолютной интегрируемости. Не вдаваясь в подробности, получим спектральное представление на основе эмпирических соображений.
Сравнивая (3.2) и (3.6) , замечаем, что бесконечная сумма ряда вырождается в единственное слагаемое b1 sin (2f0t), следовательно а0 = а1 = ... аn = 0, b2 = b3 = = ... bn = 0, лишь при n = 1, b1 = Um.
На оси частот имеем единственную точку с ненулевой амплитудой A1 при f = f0 (рис. 3.9).
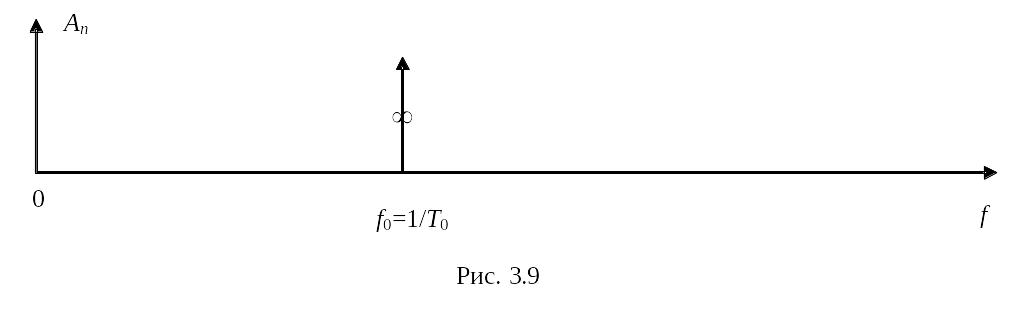
В таком случае считается, что спектр бесконечного синусоидального сигнала с постоянной амплитудой и мгновенной частотой представляет собой одну бесконечно узкую составляющую (единственную гармонику).
Примечание. На самом деле энергия сигнала, рассмотренного в примере 3.2, будет бесконечно велика, поэтому согласно закону сохранения такой же должна быть и энергия спектра. С другой стороны при бесконечной длительности синусоидального сигнала его спектральная составляющая должна иметь бесконечно малую ширину. Это невозможно для элементарных математических функций. Чтобы обойти данное противоречие в радиоэлектронике прибегают к физической абстракции – сигналу в виде -функции Дирака, обладающей бесконечной малой длительностью и бесконечно большой энергией. На рис. 3.9 приведено ее обозначение в виде стрелки с символом .
Пример 3.3. Сигнал представляет собой бесконечную последовательность гауссовых импульсов длительностью tи, следующих с интервалом Ти (рис. 3.10).
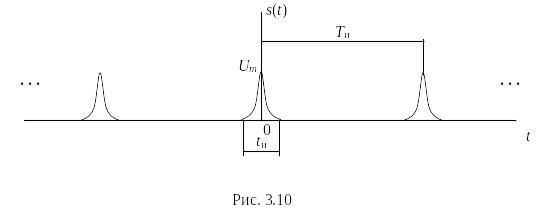
При построении спектральной диаграммы учтем то обстоятельство, что гауссовому сигналу вида 1exp(–1t 2) в частотной области соответствует тоже гауссова функция, но отличающаяся масштабом: 2exp(–2 f 2).
Второе эмпирическое правило, помогающее получить спектр данного сигнала, состоит в том, что при переходе от времени к частоте огибающей исходного сигнала будет соответствовать заполнение спектральной диаграммы, а заполнению сигнала – огибающая спектра.
Третье важное правило, сформулированное в примере 3.1, связывает масштаб сигнала и спектра: коротким сигналам соответствуют протяженные спектры и наоборот спектры сигналов с большой длительностью имеют малую ширину.
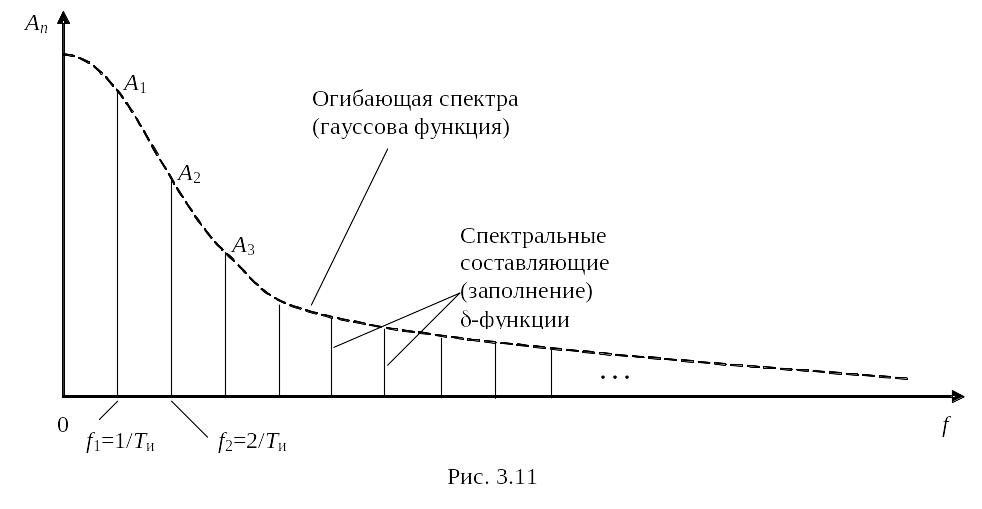
Таким образом, на оси частот относительно короткому гауссовому импульсу будет соответствовать относительно протяженная гауссова огибающая, а равномерной бесконечной огибающей соответствуют бесконечно короткие -функции заполнения, следующие с интервалом f0=1/Ти. Постоянная составляющая будет равна средней мощности сигнала.
В результате амплитудный спектр будет выглядеть так, как показано на рис. 3.11.
Пример 3.4. Рассмотрим практически важный случай бесконечной периодической последовательности прямоугольных импульсов с синусоидальным заполнением (рис. 3.12).

При построении спектральной диаграммы воспользуемся примерами 3.1, 3.2 и 3.3.
Из изложенного ранее можно сделать ряд выводов.
1. Поскольку последовательность бесконечная и периодическая, то спектральные составляющие будут представлять собой бесконечно короткие -функции следующие с интервалом по частоте равным 1/Ти.
2. Так как импульсы прямоугольные, огибающая спектра является функцией sinc(ftи).
3. Нули функции sinc(ftи) находятся в точках с координатами кратными 1/tи.
4. Поскольку заполнение синусоидальное и Ти >> T0, постоянная составляющая равна нулю.
5. И самое важное: центральная частота спектра не ноль, как во всех предыдущих примерах, а fц = 1/T0, т.е. определяется частотой синусоидального заполнения (частотой несущей).
Полный амплитудный спектр приведен на рис. 3.13.
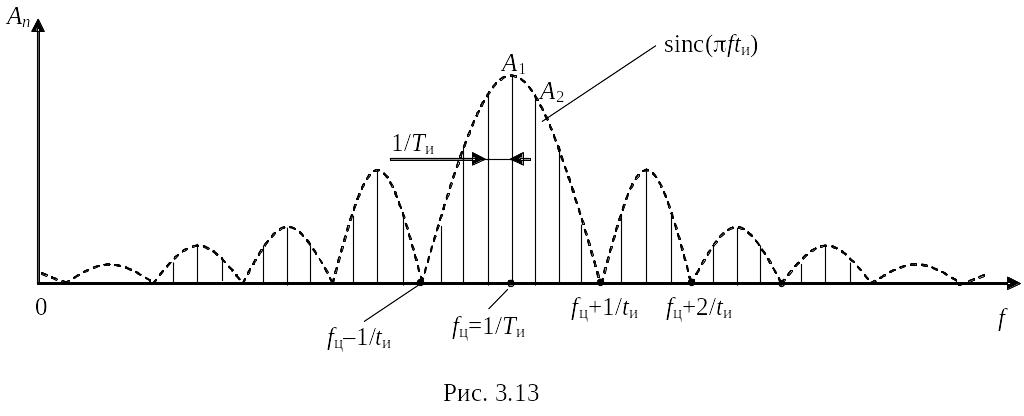
Анализируя рис. 3.13 можно понять механизм переноса спектра в ВЧ-область, реализуемый в процессе модуляции.
Исходный спектр НЧ-сигнала (см. пример 3.1) располагается в окрестности нуля частот.
Гармоническое заполнение приводит к смещению спектральных составляющих на величину fц, соответствующую частоте несущей. Структура спектра (амплитуды и фазы составляющих) при таком линейном переносе по частоте полностью сохраняется.
На этом основано использование ВЧ-несущей в радиосвязи: полезная информация, заложенная в структуру НЧ-сигнала (а следовательно и в структуру спектра) сохраняется, а сам сигнал является высокочастотным (его спектр располагается симметрично относительно частоты несущей fц) и будучи передан в антенну, порождает электромагнитные волны эффективно распространяющиеся в пространстве.
В заключение рассмотрим еще один пример, иллюстрирующий важное свойство спектров, – их суперпозицию.
Пример 3.5. Пусть сигнал представляет собой последовательность импульсов сложной формы (рис. 3.14). Требуется построить его спектральную диаграмму.
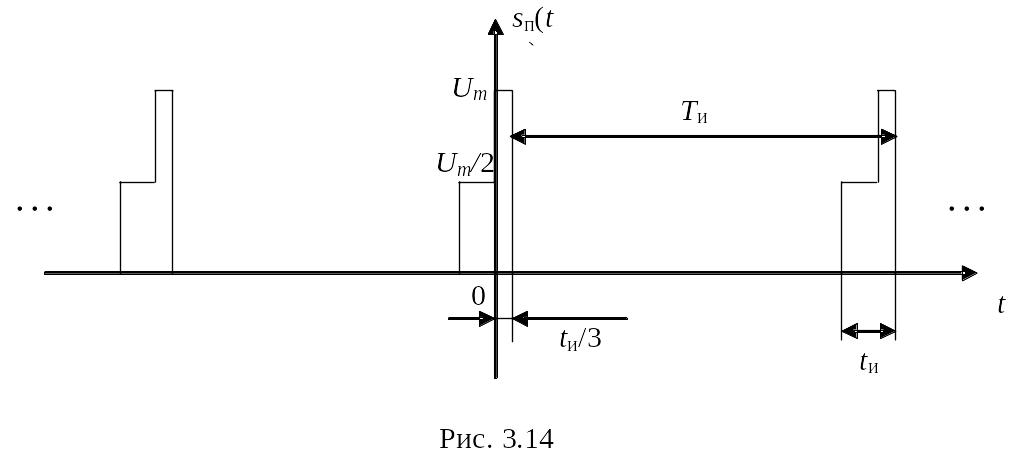
Для решения задачи сначала представим исходный сигнал в виде суммы двух вспомогательных сигналов (рис. 3.15):
sп(t) = s1(t) + s2(t).
Поскольку вспомогательные сигналы представляют собой последовательности прямоугольных импульсов, то их спектральные диаграммы легко получить по аналогии с примером 3.1, учитывая, изменение амплитуды и длительности.
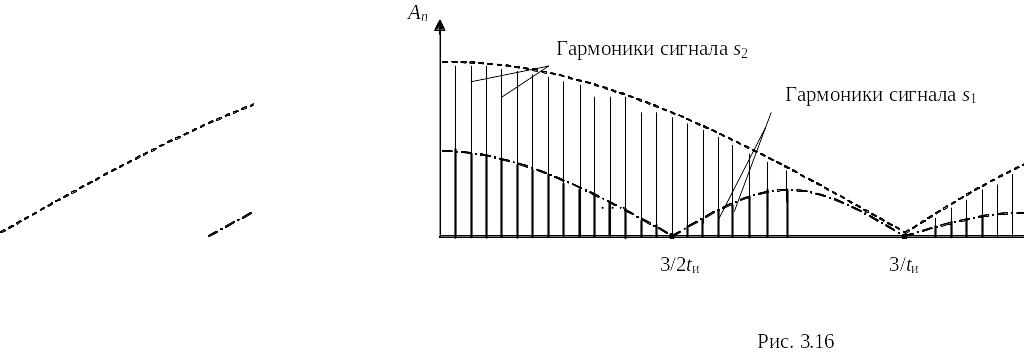
Теперь по принципу суперпозиции получим результирующую спектральную диаграмму (рис. 3.16) как сумму спектров вспомогательных сигналов.
Примечание. Для упрощения приведен только спектр амплитуд, изменение фазовых соотношений из-за смещения импульсов не учитываем.
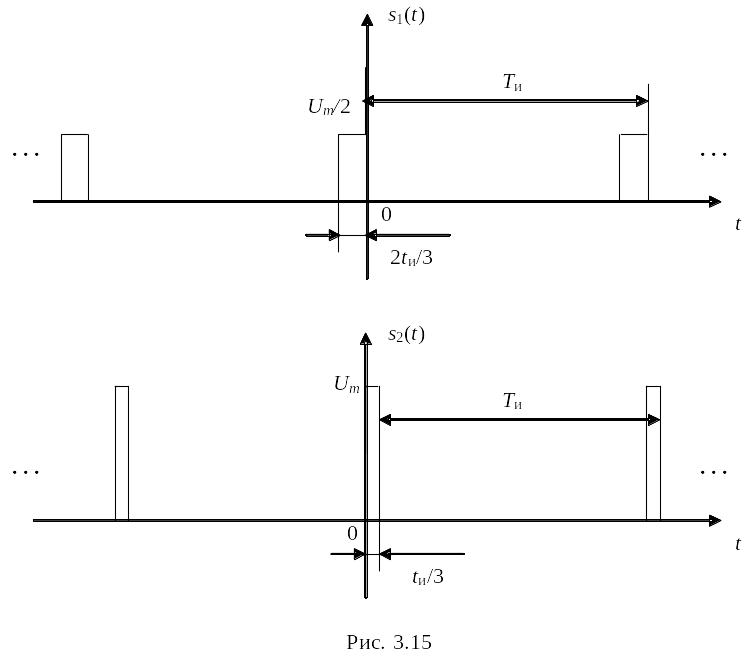
Рис. 3.15
Р ис.
3.16
ис.
3.16
На рис. 3.16 огибающая спектра сигнала s1 показана штрихпунктирной линией, огибающая спектра сигнала s2 – пунктирной линией; спектральные составляющие (гармоники) сигнала s2 изображены сплошной линией, гармоники сигнала s1 – утолщенной линией.
