Лекция 2. Сигналы и их временные модели

Основные радиотехнические процессы. Сигналы, радиосигналы и их модели. Классификация колебаний. Энергетические и информационные параметры и характеристики сигналов. Понятие базы сигнала, простые и сложные сигналы.

Основные процессы в радиотехнике (см. рис. 1.3) – фильтрация, генерация, модуляция, детектирование, кодирование и декодирование. Все радиотехнические процессы подразделяются на линейные и нелинейные. Фильтрация представляет собой пример линейного процесса, генерация – нелинейного.

На рис. 2.1 приведена классификация сигналов.

Под детерминированным понимают такой сигнал, все параметры которого (амплитуда, мгновенная частота, фаза) в заданный момент времени известны со 100%-ной вероятностью. Пример – гармонический сигнал (рис. 2.2).

Параметры случайного сигнала можно определить с вероятностью меньше 100%. Пример – белый шум (рис. 2.3).

Управляющие (модулирующие) сигналы – это сравнительно низкочастотные колебания, которые содержат полезную информацию, но непригодны для непосредственной передачи в эфир с помощью радиоволн.

Немодулированные ВЧ-колебания способны распространяться на большие расстояния, но не несут полезной информации.

Модулированные сигналы – это высокочастотные колебания один или несколько параметров которых изменяются по закону управляющего сигнала. ВЧ-колебания, в отличие от низкочастотных сигналов, иногда называют радиосигналами.

В общем случае модулированный сигнал можно представить как

s(t) = U_m(t)cos(t + (t)), (2.1)

где U_m – амплитуда сигнала,  – мгновенная частота,  – начальная фаза.

Если изменяется амплитуда, то имеем АМК – амплитудно-модулированные колебания, подробно рассмотренные далее в лекции 5.

Когда меняется мгновенная частота, получаем ЧМК – частотно-модулированные колебания.

Фазомодулированные колебания (ФМК) имеют место при изменении полной фазы по закону управляющего сигнала.

Поскольку изменение мгновенной частоты всегда приводит к изменению полной фазы и наоборот, ЧМК и ФМК по сути представляют собой две разновидности колебаний с так называемой угловой модуляцией (УМК), описанные в лекции 6.

Если меняется несколько параметров, говорят о колебаниях с комбинированной модуляцией (КМК).

Отдельную группу составляют импульсно-модулированные колебания (ИМК).

Модулирующие низкочастотные сигналы подразделяются на аналоговые, дискретные и цифровые.

Аналоговый сигнал непрерывный как по времени, так и по уровню, он существует в каждый момент времени в течение заданного интервала и принимает любое значение из определенного диапазона.

Дискретный (иногда его называют дискретизированным) сигнал непрерывен по уровню и дискретен по времени, т.е. он существует только в определенные моменты времени, число которых ограничено (счетное множество).

Дискретизированный сигнал можно подвергнуть квантованию по уровню. Значения квантованного сигнала принадлежат некоторому счетному множеству значений из заданного диапазона.

После операций дискретизации и квантования можно осуществить кодирование сигнала. В результате получаем цифровой сигнал.

На рис. 2.4 показан пример преобразования аналогового сигнала в цифровой.

Основные преимущества цифровых сигналов перед аналоговыми:

• бóльшая точность (заранее определенная погрешность, ошибки не накапливаются в процессе передачи и обработки сигнала);

• применение алгоритмов, нереализуемых в аналоговых системах, например рекурсивных;

• высокая надежность (в том числе помехоустойчивость);

• универсальность (возможность передачи информации различного рода);

• унификация (использование одинаковых структурных элементов);

• технологические, экономические, эргономические и т.п. преимущества цифровых сигналов, методов и систем обработки и передачи информации.

К недостаткам цифровых систем можно отнести повышенную сложность.

Характеристики и параметры сигналов подразделяются на энергетические и неэнергетические.

К энергетическим параметрам относятся энергия и средняя мощность.

Энергия сигнала s(t) конечной длительности равна

Э = , (2.2)

где t_н и t_к – моменты времени начала и окончания сигнала.

Для периодических сигналов используют другой параметр – среднюю мощность на некотором интервале времени (обычно его выбирают кратным периоду Т):

Р_ср = Э/Т = , (2.3)

где t₁ – произвольный текущий момент времени.

Очевидно, что формула (2.3) позволяет рассчитать среднюю мощность бесконечного сигнала.

Примеры неэнергетических параметров сигнала – мгновенная частота, начальная фаза.

Еще один важный неэнергетический параметр – база сигнала:

B = t_актf_акт, (2.4)

где t_акт – активная длительность сигнала, f_акт – активная полоса частот.

Из формулы (2.4) ясно, что база – безразмерная величина.

В зависимости от величины базы различают простые (В  1) и сложные (В >> 1) сигналы.

Поскольку в выражение (2.4) входит и время и частота, понятие базы можно рассматривать как информационную характеристику сигнала: чем больше В, тем бóльшее количество информации заложено в данный сигнал.

Пример простого радиосигнала – одиночный импульс прямоугольной формы, заполненный синусоидальной несущей. Пример сложного радиосигнала – прямоугольный импульс с частотно-модулированным заполнением.

Информационная структура сигналов, встречающихся в радиоэлектронике, весьма сложна, поэтому их анализ проводят как во временной, так и частотной области.

Собственно сигнал существует в области времени, а в частотной области ему соответствует спектр. Понятия "частотное представление сигнала" и "спектральное представление сигнала " в этом смысле являются синонимами.

Помимо параметров (одиночных численных значений) для анализа сигналов применяют функциональные зависимости – характеристики.

Наиболее часто используемые характеристики в области времени – автокорреляционная функция (АКФ) и автосвертка сигнала:

K() = s(t)  s(t) = ; (2.5)

С()= s(t) * s(t) = , (2.6)

где  – временной сдвиг.

Основные свойства АКФ:

• аргумент – временной сдвиг , а не время t;

• четная симметрия относительно оси ординат;

• максимум при  = 0 равен энергии сигнала;

• при  > t_с АКФ обращается в нуль;

• ширина АКФ обратно пропорциональна полосе частот, занимаемой спектром сигнала.

Рассмотрим примеры АКФ простейших сигналов.

Пример 2.1. Пусть сигнал представляет собой прямоугольный импульс длительностью t_и (рис. 2.5).

Вычисления по формуле (2.5) в случае сдвига в сторону запаздывания дают

K() = = ,

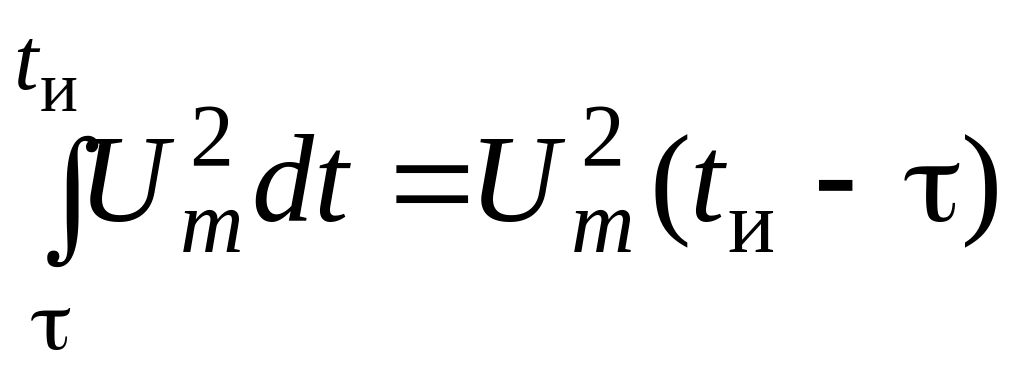где rect – прямоугольная функция.

При сдвиге в сторону опережения получаем

K() = = .

Окончательно с учетом симметрии АКФ равна

K() = . (2.7)

На рис. 2.6 приведен график АКФ прямоугольного видеоимпульса. Как видим форма АКФ треугольная с максимумом при нулевом сдвиге, функция монотонно убывает до нуля при  = t_и. Временной сдвиг t₀ не влияет на АКФ.

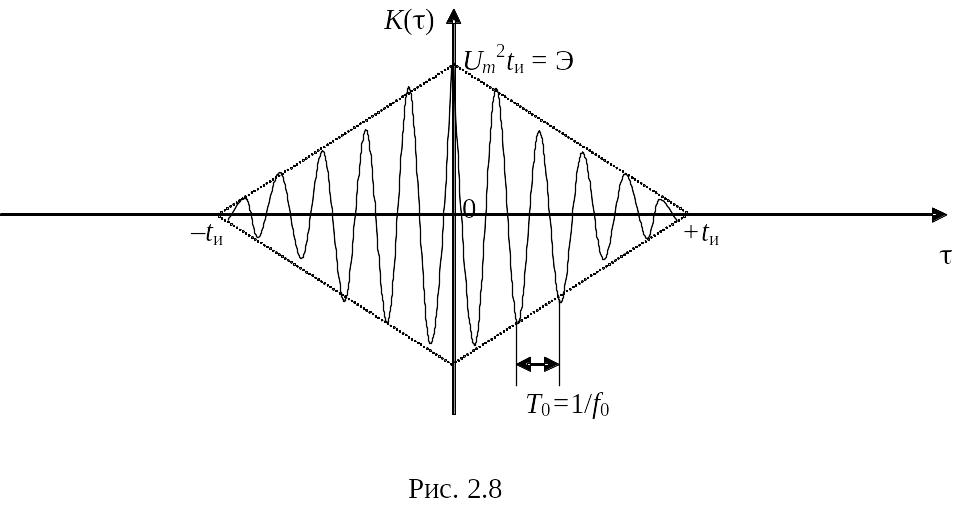
Пример 2.2. АКФ радиоимпульса длительностью t_и с синусоидальным ВЧ-заполнением с частотой f₀ (рис.2.7).

При построении графика учитываем то обстоятельство, что огибающая результирующей АКФ совпадет по форме с АКФ из примера 2.1, а заполнение будет косинусоидальным с частотой f₀. На рис. 2.8 приведен график АКФ радиоимпульса. Из рис. 2.8 видно, что функция имеет несколько локальных минимумов и максимумов.

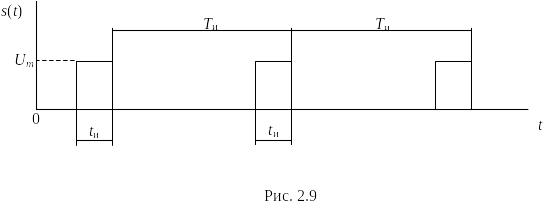
Пример 2.3. Построим АКФ пачки из трех прямоугольных импульсов длительностью t_и, следующих с интервалом Т_и (рис. 2.9).

Построение осуществляем только при сдвигах в сторону запаздывания (рис. 2.10), а результирующую функцию можно получить согласно свойству зеркальной симметрии.

Анализируя рис. 2.10 можно сделать следующие практически важные выводы:

1. АКФ пачки импульсов существует только на дискретных интервалах времени 2t_и, а в остальной области равна нулю.

2. Огибающая первичных АКФ соответствует АКФ одиночного импульса.

3. Огибающая вторичной АКФ (показана пунктиром) соответствует АКФ прямоугольного импульса длительностью, равной длительности всей пачки.

4. Максимальное значение АКФ в три раза больше, чем максимум АКФ одиночного импульса.

В заключение заметим, что АКФ существуют как для детерминированных, так и для случайных сигналов. Физический смысл АКФ заключается в том, что она дает представление об интегральной скорости изменения сигнала: чем быстрее меняется сигнал, тем ýже АКФ и наоборот.

Большое значение при анализе сигналов имеет взаимная корреляционная функция (ВКФ):

K₁₂() = s₁(t)  s₂(t) = ; (2.8)

K₂₁() = s₂(t)  s₁(t) = . (2.8а)

Здесь s₁(t) и s₂(t) – два различных сигнала.

В отличие от АКФ, взаимная корреляционная функция двух сигналов может не обладать симметрией и иметь максимум при ненулевом сдвиге. Максимальное значение ВКФ численно равно взаимной энергии сигналов.

Физический смысл ВКФ – мера сходства двух сигналов. Чем больше один сигнал похож на другой, тем больше максимум ВКФ.

Таким образом, АКФ является частным случаем ВКФ при s₁(t) = s₂(t).

Характеристики сигналов в области частот – спектральные характеристики – подробно рассматриваются далее.