7 Вопрос Непрерывные случайные величины и их числовые характеристики.

Случайная величина  называется непрерывной, если она принимает более, чем счётное число значений.

Случайная величина   называется абсолютно непрерывной, если её функция распределения может быть представлена в виде

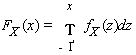. (3.24)

При этом функция   называется плотностью распределения вероятностей (или, короче, плотностью распределения) случайной величины . График плотности распределения случайной величины   называется кривой распределения вероятностей (или, короче, кривой распределения) случайной величины  . Всюду ниже в данном параграфе будут рассматриваться абсолютно непрерывные случайные величины, при этом слово <абсолютно> будет опускаться.

Как и раньше, если известно, о какой случайной величине идёт речь, то индекс, обозначающий эту случайную величину, опускается:  .

Плотность распределения обладает следующими свойствами:

для всех  :  ; (3.25)

; (3.26)

для всех точек , в которых существует производная  : . (3.27)

Вероятность того, что непрерывная случайная величина   примет конкретное числовое значение, равна нулю:

для всех  :  . ( STYLEREF 1 \s 3. SEQ Формула. \* ARABIC \s 1 28)

Вероятность попадания непрерывной случайной величины в числовой промежуток можно рассчитать по формуле

для всех  , таких, что  : (3.29)

.

Математическим ожиданием непрерывной случайной величины   называется число

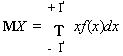. (3.30)

Математическое ожидание непрерывной случайной величины обладает теми же свойствами (3.12) - (3.15), что и математическое ожидание дискретной случайной величины.

Формулы (3.16) и (3.17) для вычисления дисперсии непрерывных случайных величин принимают вид

, (3.31)

. (3.32)

соответственно.

Дисперсия непрерывной случайной величины обладает теми же свойствами (3.20) - (3.22), что и дисперсия дискретной случайной величины.

Наиболее часто встречающиеся законы распределения непрерывных случайных величин приведены в табл. 3.2.

8 Вопрос. Нормальное распределение случайной величины. Числовые характеристики

Нормальное распределение, также называемое распределением Гаусса, —распределение вероятностей, которое играет важнейшую роль во многих областях знаний, особенно в физике. Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Ясно, что такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений, в природе чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий.

Нормальное распределение зависит от двух параметров — смещения и масштаба, то есть, является, с математической точки зрения, не одним распределением, а целым их семейством. Значения параметров соответствуют значениям среднего (математического ожидания) и разброса (стандартного отклонения).

Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1.

Характеристики распределения  Править

Плотность вероятности нормально распределённой случайной величины с параметром смещения μ и масштаба σ (или, что тоже самое, дисперсией σ²) имеет следующий вид:

Функция распределения такой величины не выражается через элементарные функции и записывается по определению через интеграл Римана как

Функция распределения стандартной нормальной случайной величины (т. е. при  ) часто обзначают как  :

Функцию распределения нормальной случайной величины с любыми параметрами легко выразить через  :

Характеристическая функция нормального распределения имеет вид

где ξ˜N(μ,σ²) — нормально распредёленная с параметрами μ и σ случайная величина.

Производящая функция моментов ξ определена для всех вещественных t задаётся формулой

Процентили стандартного нормального распределения Править

Процентили стандартного нормального распределения задаются уравнением

.

Ниже суммированы значения процентилей для наиболее чaсто встречающихся значений α.

α	0,05	0,1	0,15	0,2	0,25	0,3	0,35	0,4	0,45	0,5	0,55	0,6	0,65	0,7	0,75	0,8	0,85	0,9	0,95
zα	−1,6449	−1,2816	−1,0364	−0,8416	−0,6745	−0,5244	−0,3853	−0,2533	−0,1257	0	0,1257	0,2533	0,3853	0,5244	0,6745	0,8416	1,0364	1,2816	1,6449

Моделирование нормальных случайных величин  Править

Неточные методы моделирования основываются на центральной предельной теореме. Именно, если сложить много независимых одинаково распределённых величин с конечной дисперсией, то сумма будет распределена примерно нормально. Например, если сложить 12 независимых базовых случайных величин, получится грубое приближение стандартного нормального распределения.

Тем не менее, использование точных методов предпочтительно, поскольку у них практически нет недостатков. В частности, преобразование Бокса — Мюллера является точным, быстрым и простым для реализации методом генерации.

Статистическая проверка принадлежности нормальному распределению  Править

Поскольку нормальное распределение часто встречается на практике, то для него разработаны специальные статистические критерии: критерий Пирсона, критерий Колмогорова — Смирнова и др.

Курьёзы с нормальным распределением  Править

В популярных психологических тестах часто используются списки вопросов, ответы на которые соответствуют определённым количествам баллов, которые затем суммируются. В зависимости от суммы, испытуемого причисляют к той или иной категории. Оказывается, что согласно центральной предельной теореме, если вопросы не имеют никакого смысла и никак не соотносятся с теми категориями, к которым причисляют испытуемых, а ответы случайны (то есть, если тест фальшивый), то распределение сумм окажется приближенно нормальным, а это значит, что большинство испытуемых окажутся причислены к некоей средней категории.

Поэтому, если в каком-то тесте вы (да ещё и ваши знакомые) оказались посередине шкалы, знайте, что это, вполне возможно, сработало нормальное распределение, а тест ничего не значит.

2)Функция плотности вероятности такого нормального распределения имеет вид

Интегральная функция вероятности распределения обычно выражается через специальную функцию erf(x):