
- •1. Первообразная и неопределенный интеграл.
- •2. Определенный интеграл.
- •4. Свойство определенного интеграла – теорема о среднем. Обобщенная теорема о среднем.
- •5. Замена переменной в определенном интеграле.
- •6. Интегрирование по частям в определенном интеграле.
- •7. Определенный интеграл с переменным верхним пределом.
- •8. Формула Ньютона-Лейбница.
- •9. Интеграл ошибок.
- •10. Интегральный синус. Свойства.
- •11. Интегральный логарифм.
- •12. Интегрирование рациональных дробей.
- •16. Несобственные интегралы по неограниченному промежутку. Теоремы сравнения.
- •14. Формула прямоугольников
- •15.Формула трапеций.
- •13. Методы рационализации.
- •1. Подстановка Эйлера.
- •2. Универсальная тригонометрическая замена.
- •3. Интегрирование тригонометрических функций.
- •17. Несобственные интегралы от неограниченной функции. Свойства.
- •18. Интеграл, зависящий от параметра.
- •19. Гамма-функция.
- •20. Нахождение площади в декартовых координатах.
- •22. Нахождение объема тела вращения.
- •21. Нахождение длины дуги в декартовых и поляных координатах.
- •23. Числовые ряды. Сходимость. Остаток ряда. Необходимый признак сходимости.
- •25. Числовые ряды. Теоремы сравнения.
- •26. Теорема (признак Коши).
- •27. Теорема (признак Даламбера).
- •28.Интегральный признак сходимости.
- •30. Признак Лейбница сходимости знакочередующегося ряда.
- •29. Абсолютная сходимость. Свойства абсолютно сходящихся рядов.
- •34. Остаточный член формулы Тейлора в форме Лагранжа.
- •32. Степенные ряды.
- •37. Ряд Тэйлора для функций
- •38. Решение дифференциальных уравнений с помощью рядов. Функция Бесселя.
- •33. Ряд Тейлора. Необходимый и достаточный признаки сходимости.
29. Абсолютная сходимость. Свойства абсолютно сходящихся рядов.
Определение.
Если
ряд
![]() сходится,
то говорят, что ряд
сходится,
то говорят, что ряд![]() сходится
абсолютно. Если
сходится,
но
расходится,
то говорят, что ряд
сходится
условно.
сходится
абсолютно. Если
сходится,
но
расходится,
то говорят, что ряд
сходится
условно.
Теорема. Если ряд сходится, то и ряд сходится.
Доказательство. Запишем ряды почленно
1.
2.
![]()
Пусть
![]() -сумма
первого ряда,
-сумма
первого ряда,
![]() -сумма
второго ряда.
-сумма
второго ряда.
![]() -сумма
всех положительных,
-сумма
всех положительных,
![]() -
сумма абсолютных величин.
-
сумма абсолютных величин.
равняется разности и , -их сумме.
По
условию
имеет
предел
![]()
и - положительные возрастающие величины, меньшие .
Они
имеют пределы![]() и
и
![]() .
.
имеет
предел![]() .
Ряд сходится.
.
Ряд сходится.
Замечание. Если ряд сходится абсолютно, при любой перестановке его членов новый ряд будет по-прежнему сходиться и иметь ту же сумму.Если же ряд сходится условно, то всегда можно найти такую перестановку, что новый ряд будет сходиться к любому числу или даже станет расходящимся.
Для исследования абсолютной сходимости часто применяются признаки Коши и Даламбера, которые в этом случае имеют следующий вид.
Теорема (признак Даламбера). Если в ряде с положительными членами отношение последующего члена к предыдущему при имеет предел, т.е. то:
1.ряд АБСОЛЮТНО сходится, при l<1,
2. ряд расходится при l>1.
Теорема (признак Коши). Если в ряде с положительными членами величина имеет предел при , т.е. то:
1. ряд АБСОЛЮТНО сходится, при l<1,
2. ряд расходится при l>1.
Примечание автора. Доказательств двух последних теорем приведены в ответах на предыдущие вопросы.
34. Остаточный член формулы Тейлора в форме Лагранжа.
Формула Тэйлора выглядит следующим образом:
![]()
![]()
![]() остаточный член.
Для тех значений х, которых остаточный
член мал, многочлен дает приближенное
значение функции f(x).
остаточный член.
Для тех значений х, которых остаточный
член мал, многочлен дает приближенное
значение функции f(x).
Наша задача – оценить величину остаточного члена.
![]() где Q
– некоторая функция, подлежащая
определению.
где Q
– некоторая функция, подлежащая
определению.
Рассмотрим
вспомогательную функцию от t
![]()
![]()
![]()
Найдем производную
и преобразуем ее:
![]()
Заметим, что
![]() и
и
![]()
![]()
Подставляя,
получаем:
![]()
Это – так называемая форма Лагранжа для остаточного члена.
Так как
![]() заключено между х и а, то его можно
представить как
заключено между х и а, то его можно
представить как
![]()
![]()
32. Степенные ряды.
Определение. Степенной ряд – функциональный ряд вида
![]() где
где
![]() -
постоянные числа (коэффициенты ряда).
-
постоянные числа (коэффициенты ряда).
Область сходимости степенного ряда всегда является некоторый интервал, который, в частности, может вырождаться в точку.
Теорема
Абеля. Если
степенной ряд сходится (расходится)
при некотором значении
![]() то
он абсолютно сходится (расходится) при
всяком значении х, для которого
то
он абсолютно сходится (расходится) при
всяком значении х, для которого
![]()
![]()
Доказательство.
Так как, по предположению, числовой ряд
сходится
![]() то
общий член
то
общий член![]() при
при
![]() Это
значит, что существует такое положительное
число М, что все члены по абсолютной
величине меньше М.
Это
значит, что существует такое положительное
число М, что все члены по абсолютной
величине меньше М.
Перепишем ряд в
следующем виде:
![]()
Рассмотрим ряд из
абсолютных величин его членов:
![]()
Члены этого ряда
меньше соответствующих членов ряда![]()
При
последний
ряд представляет собой геометрическую
прогрессию со знаменателем![]() и,
следовательно, сходится. Отсюда сходится
и
и,
следовательно, сходится. Отсюда сходится
и
Это значит, что ряды и сходятся абсолютно.
___
Нетрудно будет доказать и второй случай (когда ряд расходящийся).
Доказательство.
Пусть в некоторой точке
ряд![]() расходится. Тогда он будет расходиться
в любой точке, удовлетворяющей условию
расходится. Тогда он будет расходиться
в любой точке, удовлетворяющей условию![]()
___
Теорема Абеля
позволяет судить о расположении точек
сходимости и расходимости степенного
ряда. Если
-
точка сходимости, то весь интервал![]() заполнен
точками абсолютной сходимости и
наоборот.
заполнен
точками абсолютной сходимости и
наоборот.
Теорема (о строении области сходимости степенного ряда). Областью сходимости степенного ряда является интервал с центром в начале координат.
Определение. Интервал сходимости степенного ряда – интервал от –R до +R, что для всякой точки х, лежащей внутри, ряд сходится, и притом абсолютно, а для точек вне интервала – ряд расходится. Число R – радиус сходимости ряда.
Отметим, что у
некоторых рядом интервал сходимости
вырождается в точку (R=0),
у других охватывает всю ось Ох
![]()
Теорема.
Степенной ряд
мажорируем
на любом отрезке![]() целиком
лежащем внутри интервала сходимости.
целиком
лежащем внутри интервала сходимости.
Определение. Ряд называется мажорируемым, если каждый его член по абсолютной величине не больше соотвествующего члена некоторого сходящегося числового ряда с положительными членами.
Доказательство.
По условию![]() а
потому ряд (с положительными членами)
сходится. Но при
а
потому ряд (с положительными членами)
сходится. Но при![]() члены
ряда по абсолютной величине не больше
соответствующих членов ряда
члены
ряда по абсолютной величине не больше
соответствующих членов ряда
![]()
Следовательно,
ряд мажорируем на отрезке
![]()
Следствие1. На всяком отрезке, целиком лежащем внутри интервала сходимости, сумма степенного ряда есть непрерывная функция.
Это связано с тем, что члены ряда – непрерывные функции от х. Тогда и сумма этого ряда есть непрерывная функция.
Следствие2.
Если пределы интегрирования![]() лежат
внутри интервала сходимости, то интеграл
от суммы ряда равен сумме интегралов
от членов ряда. Так как область
интегрирования можно заключить в
отрезок
лежат
внутри интервала сходимости, то интеграл
от суммы ряда равен сумме интегралов
от членов ряда. Так как область
интегрирования можно заключить в
отрезок
Дифференцирование степенных рядов.
Теорема 1.Если
степенной ряд
![]() имеет
имеет
интервал сходимости
(-R,R),
то ряд
![]() полученный почленным дифференцированием
первого ряда, имеет тот же интервал
сходимости (-R,R).
При этом
полученный почленным дифференцированием
первого ряда, имеет тот же интервал
сходимости (-R,R).
При этом
![]() если
если
![]() ,
т.е. внутри инервала сходимости
производная от суммы степенного ряда
равна сумме ряда, полученного почленным
дифференцированием ряда
.
,
т.е. внутри инервала сходимости
производная от суммы степенного ряда
равна сумме ряда, полученного почленным
дифференцированием ряда
.
31. Приближенное нахождение суммы числового ряда.
Существуют два основных способа вычислять сумму сходящихся числовых рядов с заданной точностью (в зависимости от использованного признака сходимости).
1. Признак Коши.
1Определим К.
![]()
2Выберем q.
![]()
3Возьмем минимальное
![]() Для любого n
Для любого n
![]()
4Определим
минимальное m
(натуральное), чтобы
![]()
5Возьмем
![]()
Сумма n0
членов даст сумму ряда с точностью
![]()
2. Признак Даламбера.
1Определим D.
![]()
2Выберем
q.
![]()
3Возьмем минимальное
Для любого
![]()
![]()
4Определим
минимальное m
(натуральное), чтобы
![]()
5Возьмем
![]()
Сумма n0 членов даст сумму ряда с точностью
P.S. В методическом пособии по курсу «мат. анализ» рассмотрены только эти 2 способа.
35. Разложение функций в ряд Тэйлора.
Формула Тэйлора выглядит следующим образом:
![]()
Для разложения какой-либо функции находятся последовательные производные и подставляются в известную формулу.
Отметим также, что
каково бы ни было х, остаточный член
![]() при
при
![]()
Пример.
![]()
Находим последовательные производные.

Подставляя значения, получаем:
![]()
36. Ряд Тэйлора
для функций
![]()
1.
![]()
Находим последовательные производные.
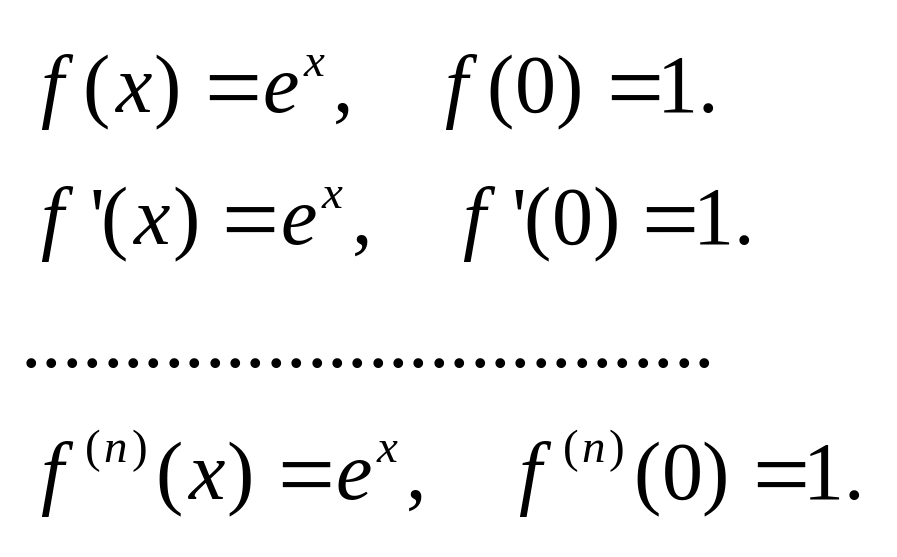
Подставляя выражения
в формулу Тэйлора получаем:
![]()
Таким образом, взяв достаточное число членов, мы можем вычислить значение функции с любой степенью точности.
2.
Находим последовательные производные.
Подставляя значения, получаем:
3.
![]()
Аналогично разложению синуса, получаем:
![]()
