
- •7. Обыкновенные дифференциальные уравнения
- •7.1. Простейшие дифференциальные уравнения и методы их интегрирования.
- •7.1.1 Основные понятия теории дифференциальных уравнений.
- •7.1.2. Дифференциальные уравнения первого порядка.
- •Понятие об изогональных траекториях.
- •7.5. Интегрирование простейших типов д.У. 1-го порядка.
- •7.5.1. Д.У. С разделяющимися переменными.
- •7.5.2. Однородные д.У. 1-го порядка.
- •7.5.3. Линейные уравнения 1-го порядка.
- •7.5.5. Д.У. В полных дифференциалах.
- •3.1. Общие положения.
- •9. Линейные д.У..
- •9.1. Введение.
- •9.2.2. Фундаментальная система решений однородного линейного д.У.
- •9.2.3. Формула Остроградского-Лиувилля Пусть и – решения (2), следовательно,
- •9.2.4. Существование фср (2)
- •9.2.5. Применение формулы Остроградского-Лиувилля
- •9.3. Линейные неоднородные дифференциальные уравнения 2-го порядка
- •9.3.1. Теоремы о частных решениях
- •9.3.2. Метод вариации произвольных постоянных для нахождения частного решения неоднородного дифференциального линейного уравнения 2-го порядка
- •9.4. Линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами и приводящиеся к ним
- •9.4.1. Интегрирование однородных линейных дифференциальных уравнений 2-го порядка с постоянными коэффициентами
- •9.4.2. Неоднородные линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами
- •В силу следствия достаточно найти решение уравнения
- •9.4.3. Линейные дифференциальные уравнения, приводящиеся к уравнениям с постоянными коэффициентами
- •9.4.4. Линейные дифференциальные уравнения n-го порядка
- •9.5. Системы дифференциальных уравнений
9.2.3. Формула Остроградского-Лиувилля Пусть и – решения (2), следовательно,
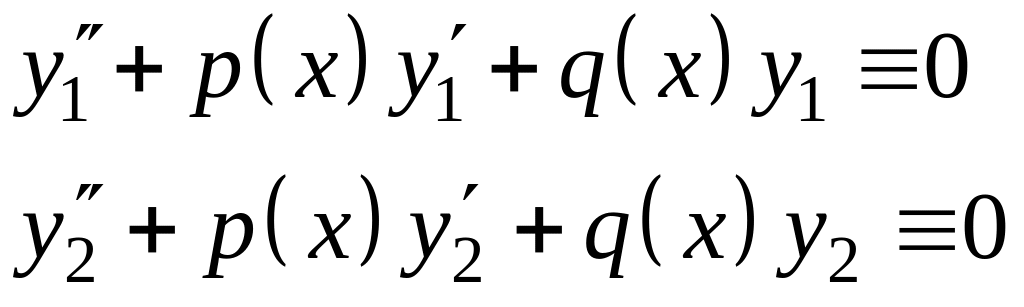 . (3)
Умножим
первое из этих уравнений на
. (3)
Умножим
первое из этих уравнений на
![]() ,
а второе – на
и сложим их, получим
,
а второе – на
и сложим их, получим
![]() , (
, (![]() )
что
равносильно
)
что
равносильно
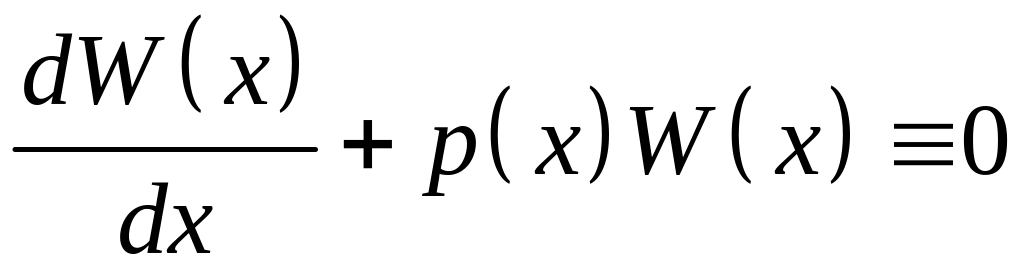 . (
. (![]() )
)
Это
означает, что
![]() двух решений уравнения (2) есть одно из
решений дифференциального уравнения
(1). Рассмотрим уравнение
двух решений уравнения (2) есть одно из
решений дифференциального уравнения
(1). Рассмотрим уравнение
![]() . (
. (![]() )
)
Решая его, получим:
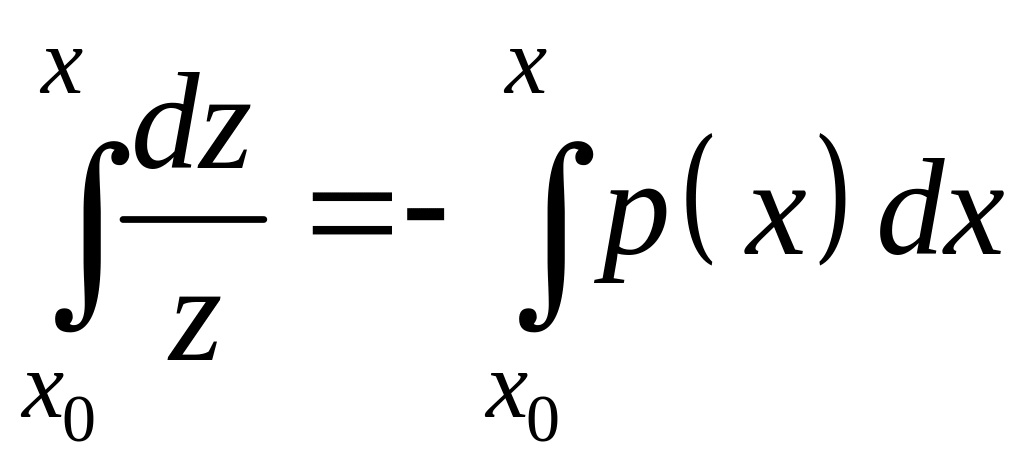
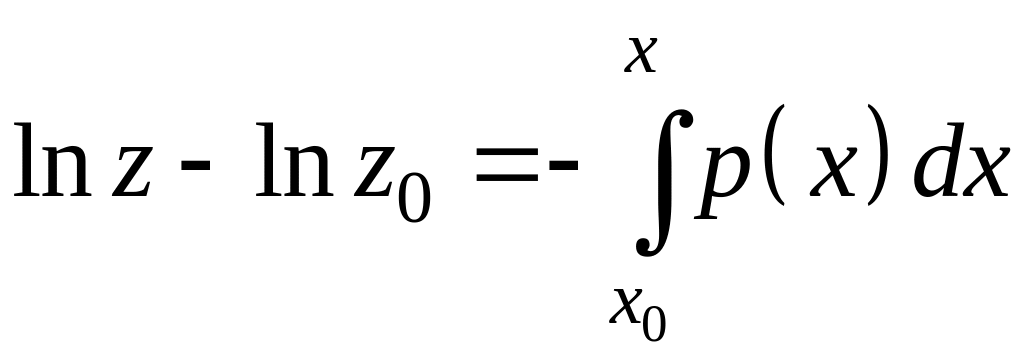
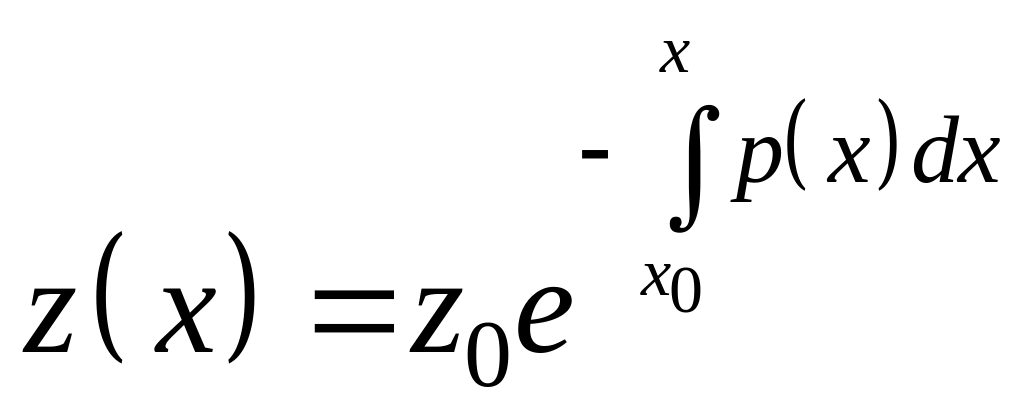 .
.
Поскольку
начальное условие
![]() произвольно, то и
произвольно, то и
![]() является фактически произвольной
константой:
является фактически произвольной
константой:
![]() .
.
Так как определитель Вронского есть одно из решений ( ), то для него также справедлива следующая формула:
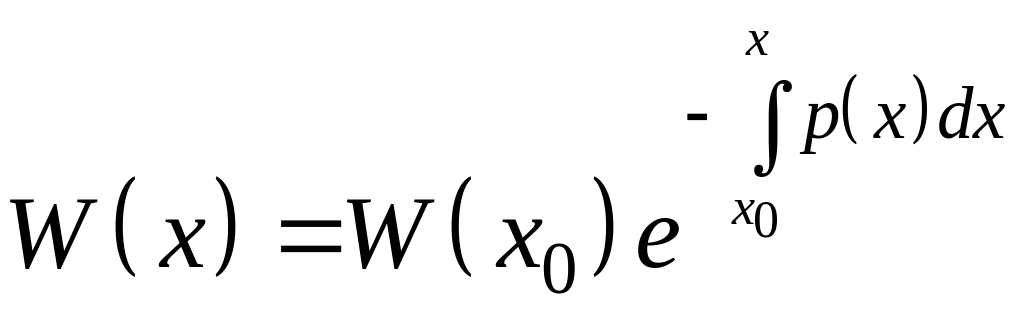 . (4)
. (4)
Формула Остроградского-Лиувилля справедлива для любых двух решений уравнения (2).
Функция
![]() непрерывна, следовательно,
непрерывна, следовательно,
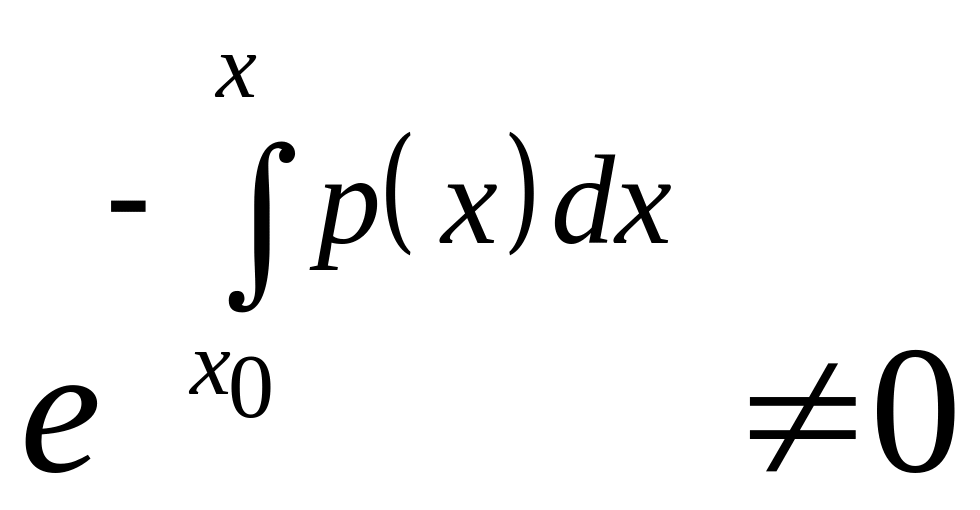 и справедливо следующее утверждение:
вронскиниан
либо тождественно равен нулю, если
и справедливо следующее утверждение:
вронскиниан
либо тождественно равен нулю, если
![]() ,
либо не равен нулю ни при одном
,
либо не равен нулю ни при одном
![]() ,
если
,
если
![]() .
Таким образом, определитель Вронского
для фундаментальной системы решений
не только тождественно не равен нулю,
но и не обращается в ноль ни при одном
.
Существенной является непрерывность
.
.
Таким образом, определитель Вронского
для фундаментальной системы решений
не только тождественно не равен нулю,
но и не обращается в ноль ни при одном
.
Существенной является непрерывность
.
9.2.4. Существование фср (2)
Теорема:
Любое однородное линейное дифференциальное уравнение имеет фундаментальную систему решений.
Доказательство:
Рассмотрим дифференциальное уравнение
![]()
и две системы начальных условий:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где
 .
.
Пусть и – частные решения соответствующих задач Коши. Докажем, что они образуют фундаментальную систему:
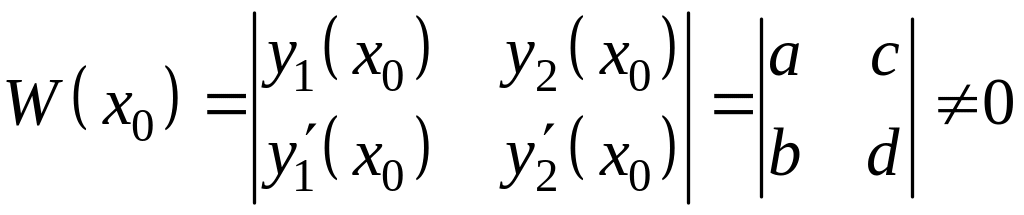 .
.
Теорема доказана.
Основная теорема:
Общее решение линейного однородного дифференциального уравнения 2-го порядка является линейной комбинацией с произвольными постоянными коэффициентами любых двух решений этого уравнения, образующих фундаментальную систему решений. Другими словами, общее решение линейного однородного дифференциального уравнения 2-го порядка есть сумма двух частных решений линейно независимых решений, умноженных на произвольные постоянные.
Доказательство:
Пусть
и
![]() – фундаментальная система решений.
Составим линейную комбинацию
– фундаментальная система решений.
Составим линейную комбинацию
![]() ,
,
где
![]() ,
,
![]() есть произвольные постоянные. Надо
доказать, что любое частное решение
можно получить из
есть произвольные постоянные. Надо
доказать, что любое частное решение
можно получить из
![]() выбором
и
.
выбором
и
.
Пусть
![]() есть решение задачи Коши для начальных
условий
есть решение задачи Коши для начальных
условий
,
![]() ,
,
![]() .
.
Положим , тогда
![]() ,
,
![]() ,
,
отсюда
 и
и
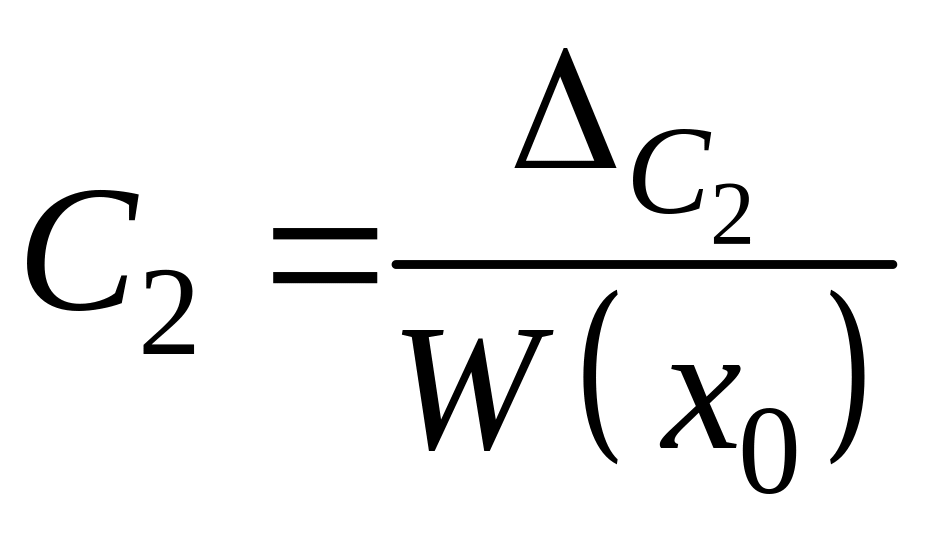 .
.
Так как , то и есть общее решение.
9.2.5. Применение формулы Остроградского-Лиувилля
Зная одно частное решение (2), не равное нулю, можно с применением формулы Остроградского-Лиувилля найти фундаментальную систему и, следовательно, общее решение (2), вычислив два неопределённых интеграла.
Пусть
![]() есть известное решение и нужно найти
есть известное решение и нужно найти
![]() .
Так как
.
Так как
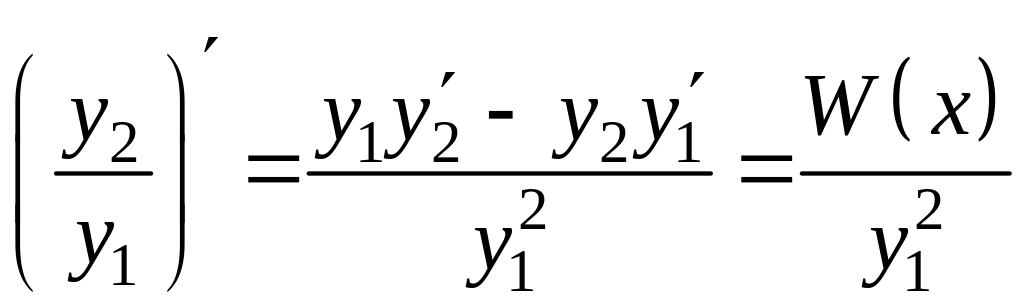 и
и
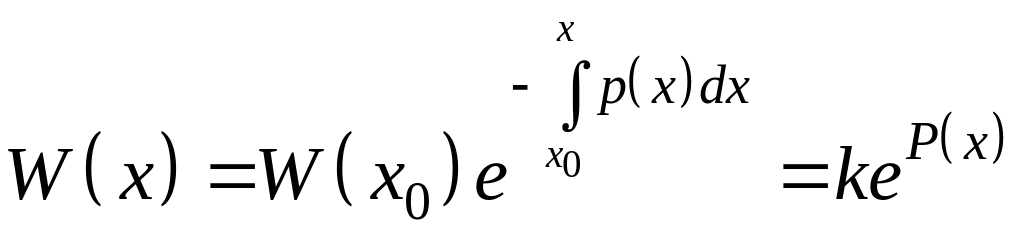 ,
то при
,
то при
![]() получаем:
получаем:
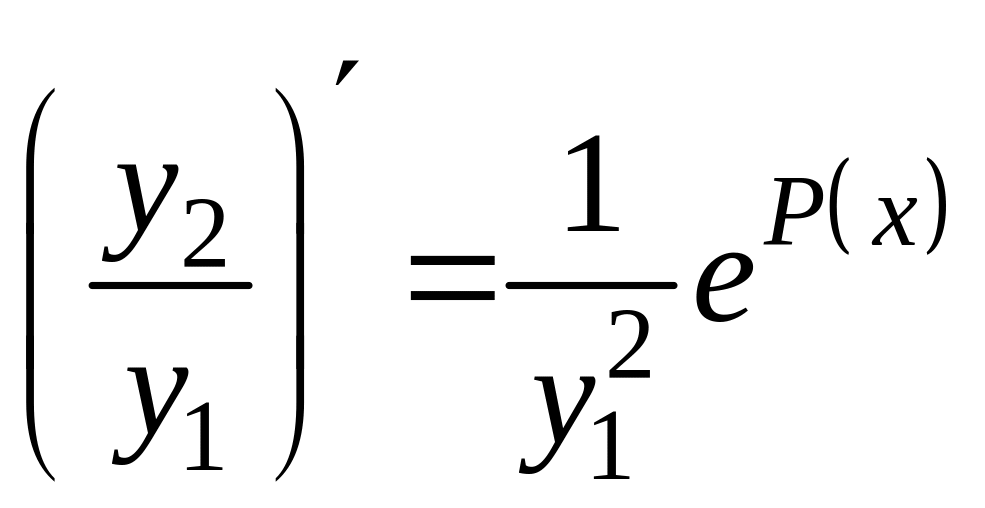
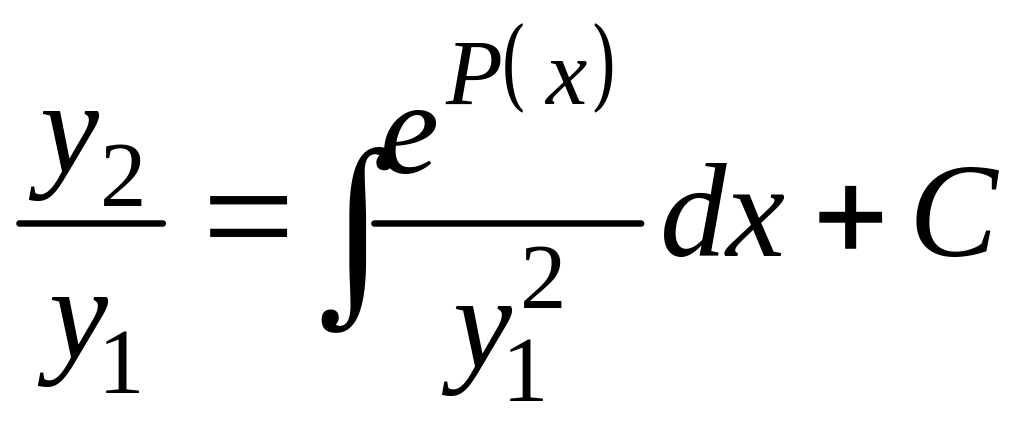 .
.
И, наконец, при
![]()
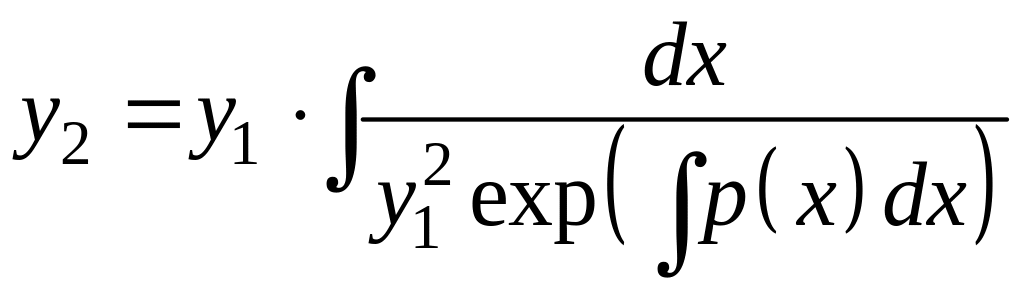 .
.
Пример. Рассмотрим дифференциальное уравнение
![]() ,
,
![]() .
.
Тогда
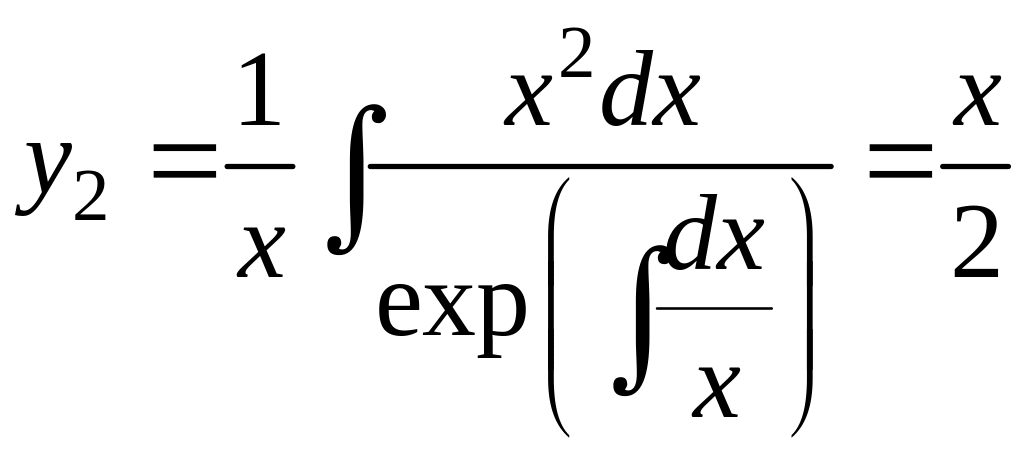 .
.
Общее решение будет:
![]() .
.
9.3. Линейные неоднородные дифференциальные уравнения 2-го порядка
9.3.1. Теоремы о частных решениях
Рассмотрим неоднородное уравнение
![]() (1)
(1)
и соответствующее однородное уравнение
. (2)
Теорема 1:
Разность любых двух частных решений уравнения (1) есть частное решение соответствующего однородного дифференциального уравнения.
Доказательство:
Пусть
и
– частные решения уравнения (1). Подставим
в соответствующее однородное
дифференциальное уравнение функцию
![]() вместе с ее производными:
вместе с ее производными:
![]() .
.
Теорема доказана.
Теорема 2:
Если
![]() – частное решение уравнения (1),
– частное решение уравнения (1),
![]() – частное решение соответствующего
однородного уравнения, то
– частное решение соответствующего
однородного уравнения, то
![]()
есть новое частное решение уравнения (1).
Доказательство:
Справедливы следующие соотношения:
![]() ,
,
![]() ,
,
значит,
![]() .
.
Теорема доказана.
Из теорем 1 и 2 следует, что, взяв любое одно частное решение неоднородного уравнения (1) и прибавляя всевозможные частные решения однородного уравнения (2), получим все без исключения частные решения уравнения (1).
Определение: Общее решение неоднородного линейного дифференциального уравнения 2-го порядка есть сумма любого частного решения данного уравнения и общего решения соответствующего однородного линейного дифференциального уравнения 2-го порядка:
![]() ,
,
где и есть линейно независимые частные решения уравнения (2).
Теорема 3:
Если
правая часть уравнения (1) есть сумма
двух функций
![]() и
и
![]() ,
и если
,
и если
![]() есть частное решение уравнения (1) с
правой частью
,
а
есть частное решение уравнения (1) с
правой частью
,
а
![]() – частное решение уравнения (1) с правой
частью
,
то
– частное решение уравнения (1) с правой
частью
,
то
![]() – частное решение уравнения (1) с правой
частью
– частное решение уравнения (1) с правой
частью
![]() .
.
Доказательство:
Рассмотрим
уравнение
![]() ,
подставим
и
в уравнения
,
подставим
и
в уравнения
![]() и
и
![]() соответственно. После сложения последних
уравнений и группировки слагаемых
получим:
соответственно. После сложения последних
уравнений и группировки слагаемых
получим:
![]() .
.
Теорема доказана.
Пример:
![]() , (1)
, (1)
![]() ,
,
![]() , (2)
, (2)
![]() ,
,
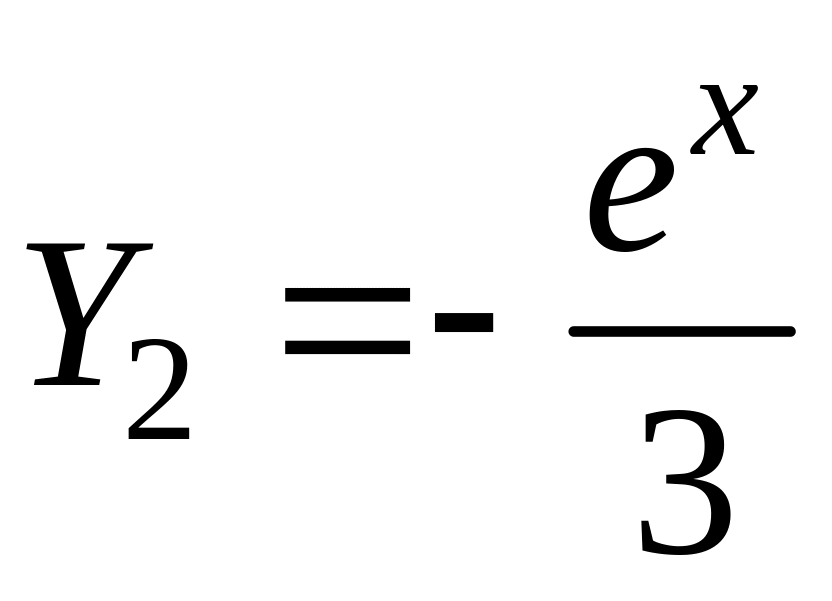 . (3)
. (3)
Тогда
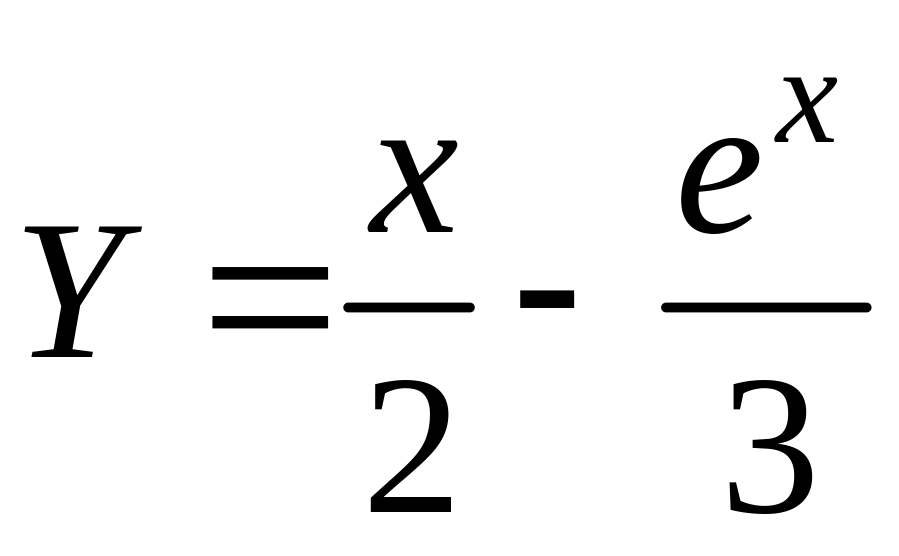 – частное решение уравнения (1).
– частное решение уравнения (1).
