9.5. Системы дифференциальных уравнений

9.5.1. …

Нормальной системой дифференциальных уравнений называют систему дифференциальных уравнений 1-го порядка с неизвестными функциями , , …, аргумента , в которой любое уравнение содержит производную 1-го порядка только от одной из функций:

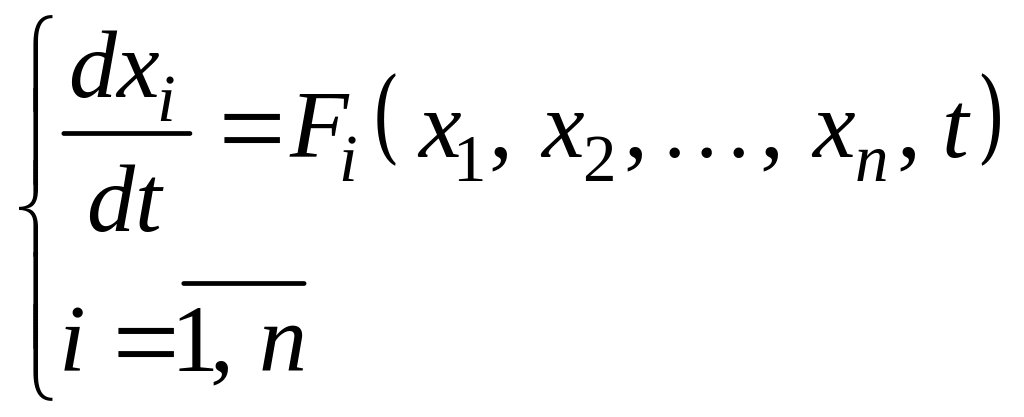. (1)

Теорема Коши.

Если – непрерывные функции по , , …, в некоторой области , то любой внутренней точке области соответствует, и притом единственное, решение , , …, , удовлетворяюще этим начальным условиям. Такое решение называется частным.

Произвольно изменяя , получим бесконечное множество решений, или:

, …,

– такое решение называется общим. Частное решение всегда можно получить из общего.

Системы дифференциальных уравнений типа (1) и дифференциальные уравнения -го порядка можно преобразовывать друг в друга с помощью введения дополнительных переменных или их исключения.

Нормальная система линейных дифференциальных уравнений с постоянными коэффициентами имеет вид:

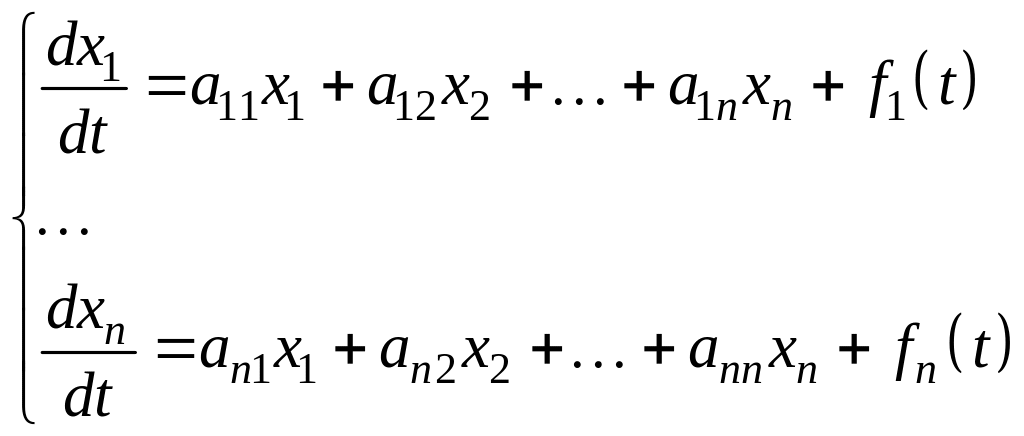(2)

– действительные числа, – известные непрерывные функции. Если , то система называется однородной.

Рассмотрим метод интегрирования системы (2) приведением е к одному линейному дифференциальному уравнению -го порядка с одной искомой функцией (например). Для этого продифференцируем первое уравнение из (2) по и заменим получившиеся в правой части их выражениями из (2):

.

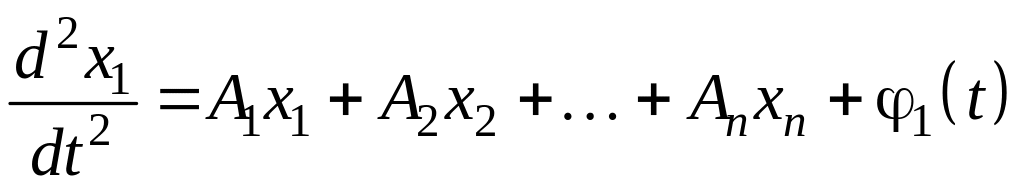Затем продифференцируем и его по и снова сделаем замены. После -го шага получим систему:

(*)

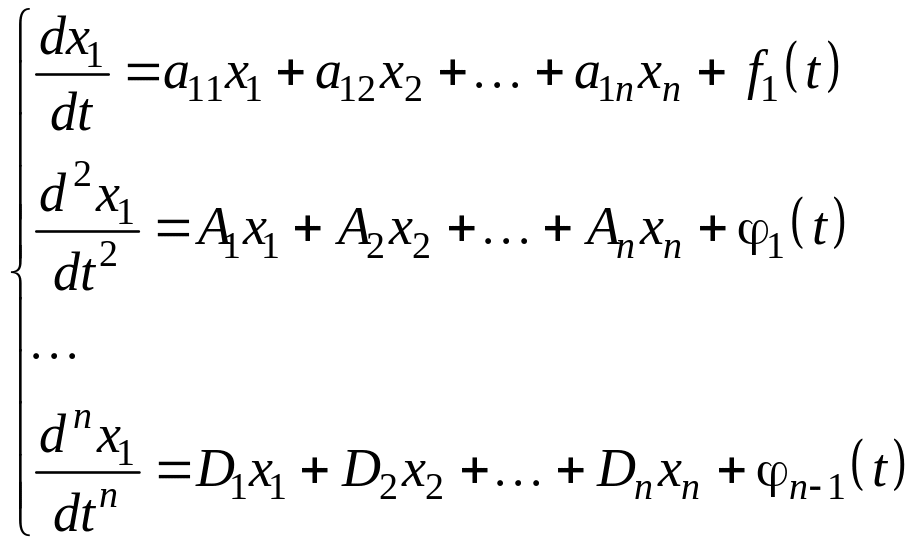Выражая из первых уравнений , , …, через , , , , …, 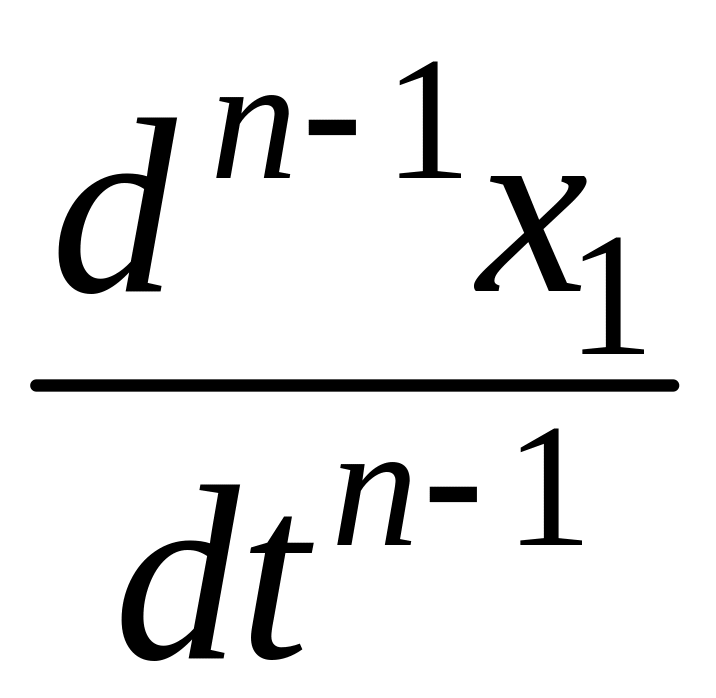(предполагая ) и подставляя в -е уравнение, получим

(**)

– линейное дифференциальное уравнение -го порядка с постоянными коэффициентами и одной неизвестной функцией.

Найдя общее решение (**) и используя производные 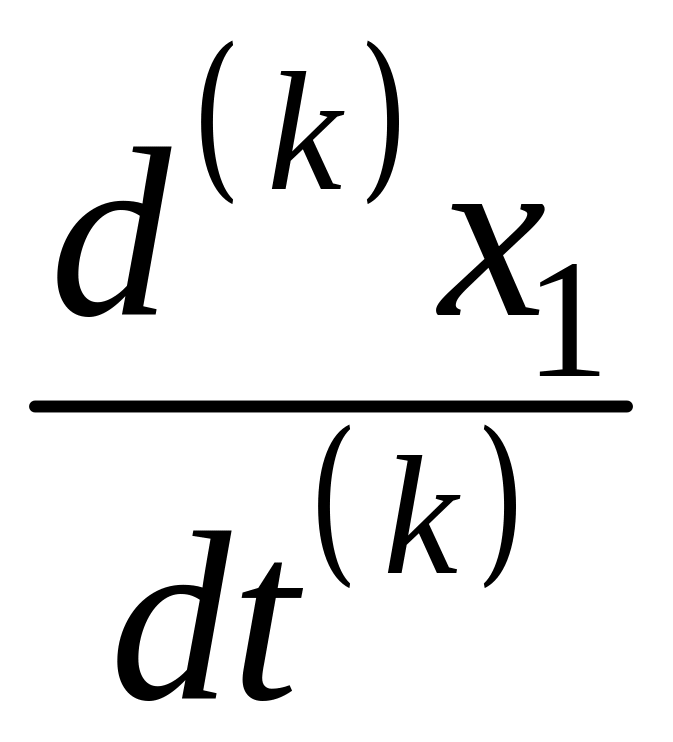от него из (*) найдем , , …, .

Пример.

,

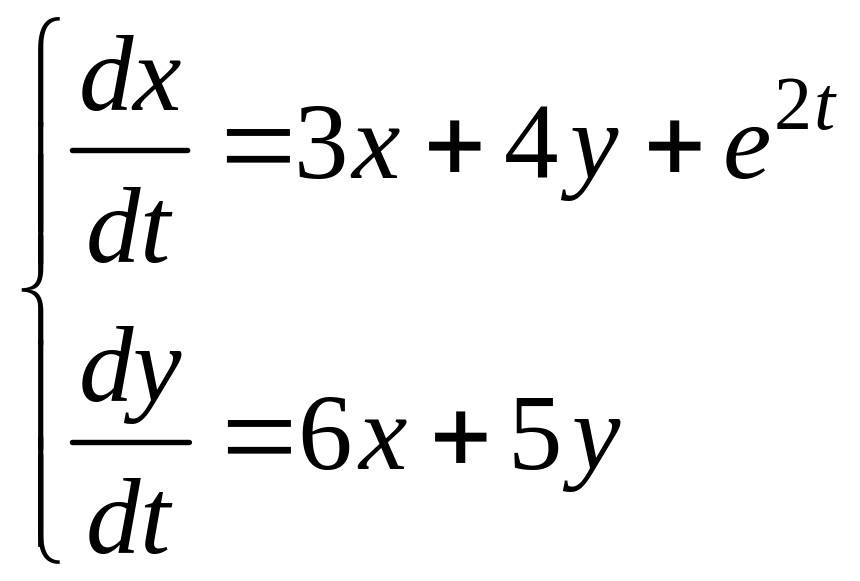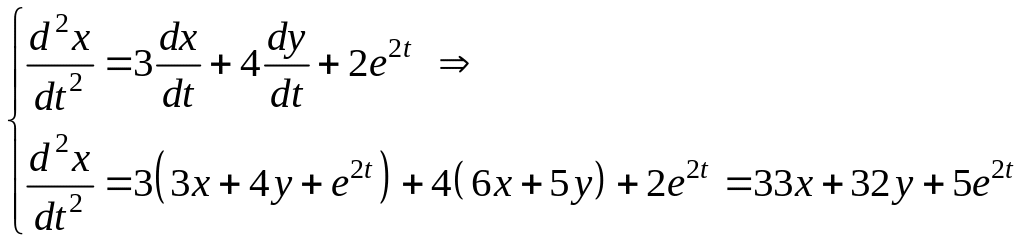
Получим систему

,

.

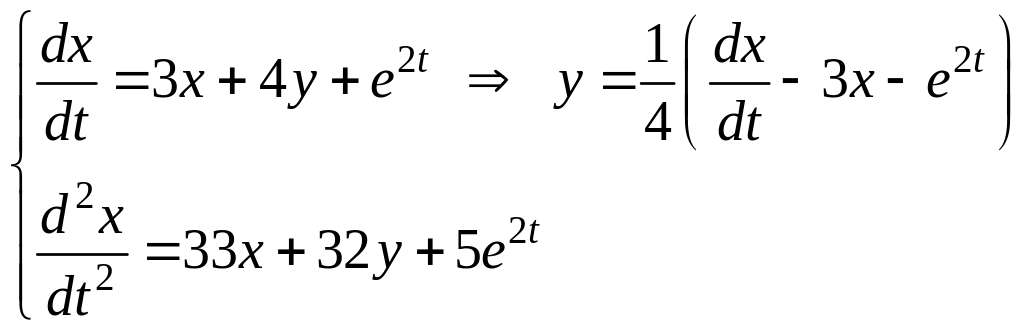Дифференцируя и подставляя в , найдем:

.

36