9. Линейные д.У..

9.1. Введение.

Линейное д.у. n-го порядка имеет вид:

(1)

где y – неизвестная функция аргумента x, - заданные непрерывные функции. Линейное д.у. называется однородным, если .

При - уравнение неоднородно, или уравнение с правой частью.

Задачу нахождения решения, отвечающего условиям:

при называют задачей Коши для д.у. n-

го порядка.

Теорема Коши: Если в д.у. n-го порядка

функция F непрерывна, а ее частные производные по ограничены во всех точках (n+1) – мерной области , то для любого существует единственное решение данного д.у., удовлетворяющее начальным условиям.

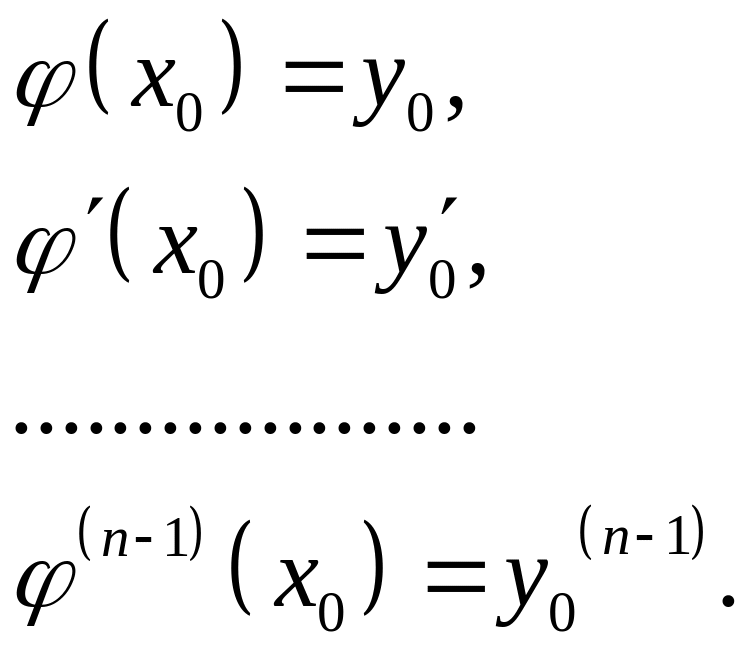
Такое решение называют частным решением, соответствующим заданным начальным условиям.

Общим решением д.у. n-го порядка ( определенным на D, где выполнены условия теоремы Коши ) называют решение этого уравнения, зависящего от n произвольных постоянных

и являющихся совокупностью всех частных решений данного д.у.. Существование общего решения также гарантируется теоремой Коши, при соблюдении ее условий.

Для получения частного из общего необходимо найти . Естественно, что условия теоремы Коши выполняются для линейного д.у. n-го порядка в области непрерывности его коэффициентов. Расшифровать!

9.2. Линейные однородные д.у. 2-го порядка.

9.2.1. Теоремы о частных решениях.

Рассмотрим линейное однородное д.у. 2-го порядка :

(2)

Имеют место следующие теоремы:

Теорема 1. Всякая линейная комбинация

нескольких частных решений однородного д.у. 2-го порядка также является его решением.

Доказательство: Подставляя y в (2) и группируя:

т.к теорема доказана.

В частности сумма и разность 2-х частных решений также является решеиями. Например - являются решениями д.у. , т.к. и - решения.

Теорема 2. Если известно одно частное решение д.у. однородного ( ненулевое ), то можно понизить порядок этого д.у. на единицу.

Док-во: Подстановка , где z – новая неизвестная функция приведет к :

подставляя получим:

Далее, пусть и и разделим все уравнение на тогда:

, где т.е. получили д.у. 1-го порядка относительно u.

9.2.2. Фундаментальная система решений однородного линейного д.У.

Определение: Ф.С.Р. однородного д.у. 2-го порядка называется всякая пара частных решений этого уравнения, отношение которых не равно постоянной. Такие решения также называют линейно-независимыми.

Например:

и частные решения образуют

Ф.С.Р., а

и - нет.

Если - Ф.С.Р. то - также будет Ф.С.Р.

Действительно, пусть 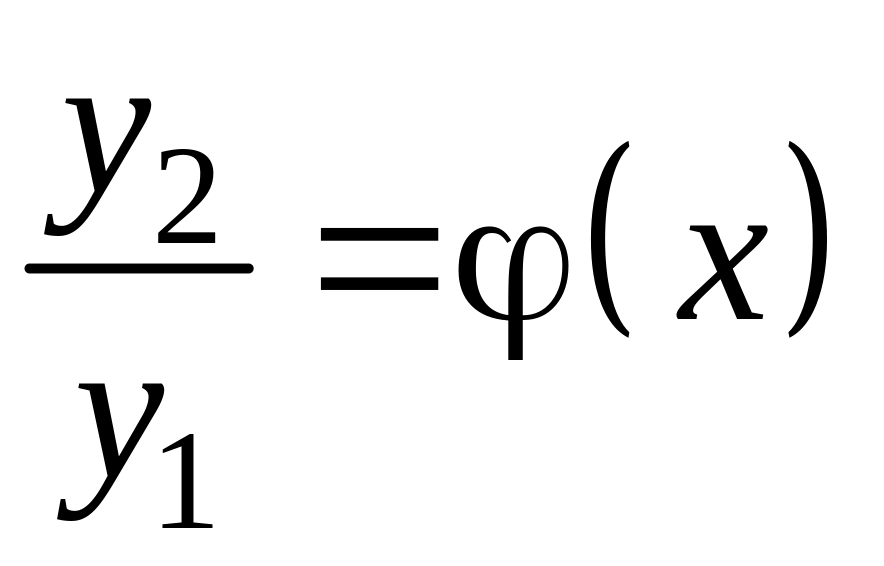, где , но тогда , что и требовалось доказать.

Таким образом, если уравнение имеет одну ФСР, то оно имеет их бесконечно много. Всякое дифференциальное линейное однородное уравнение имеет нулевое решение , но оно не входит ни в одну фундаментальную систему.

Определение: Определителем Вронского (вронскинианом) системы двух частных решений и уравнения (2) называют

.

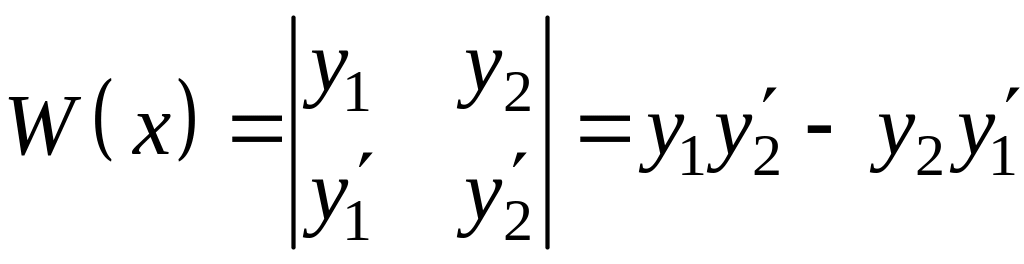Свойства определителя Вронского:

1. Если и не образуют фундаментальной системы (т.е. являются линейно зависимыми, то их определитель Вронского тождественно равен нулю:

.

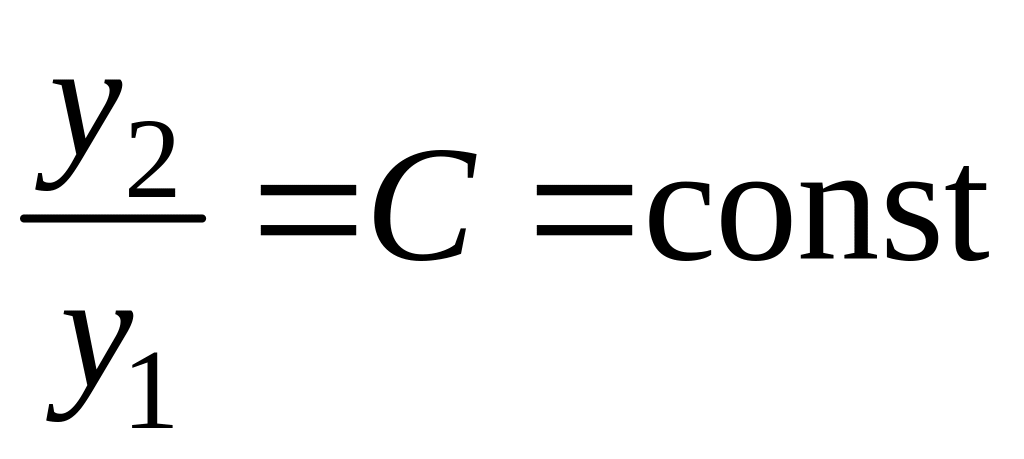
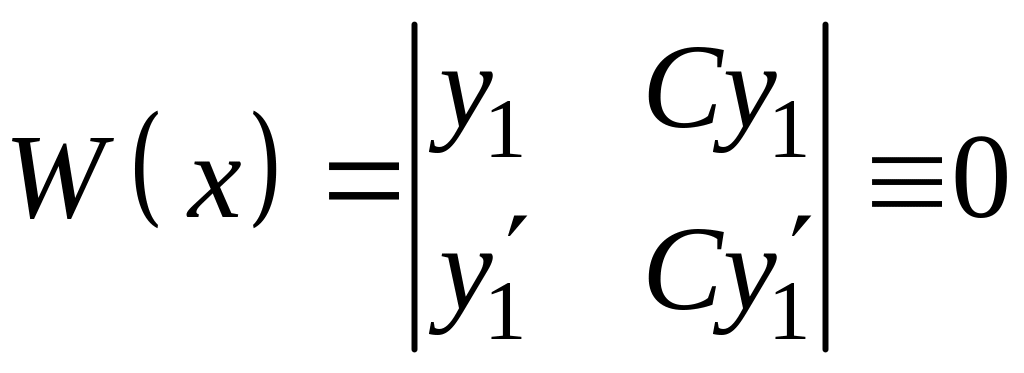2. Если 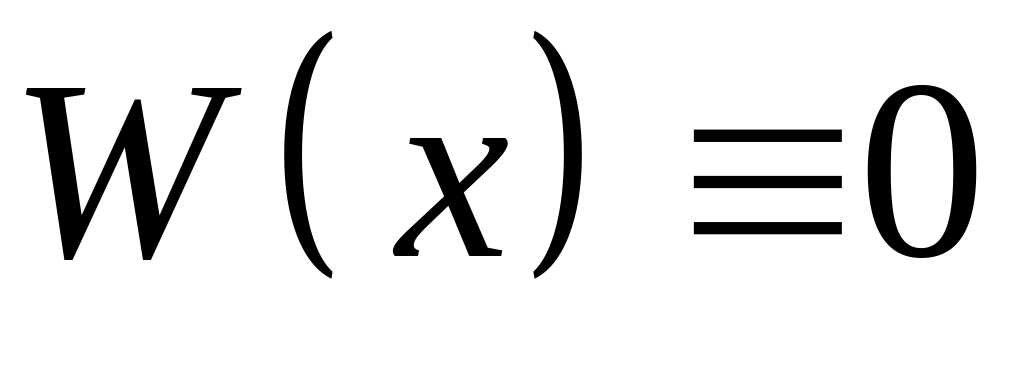, то решения и – линейно зависимы.

Пусть 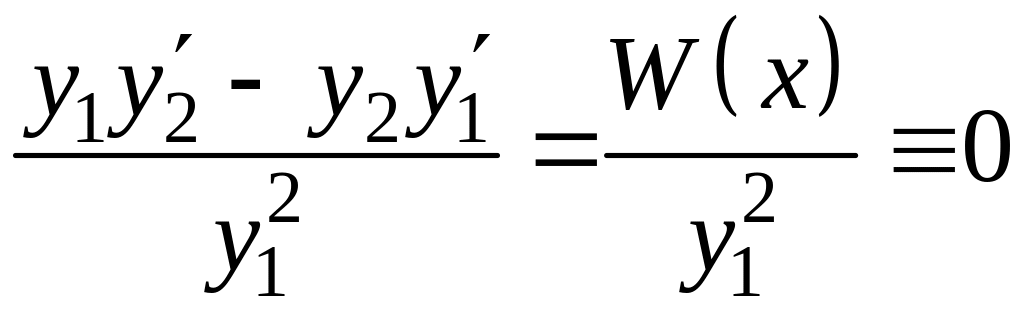или

.

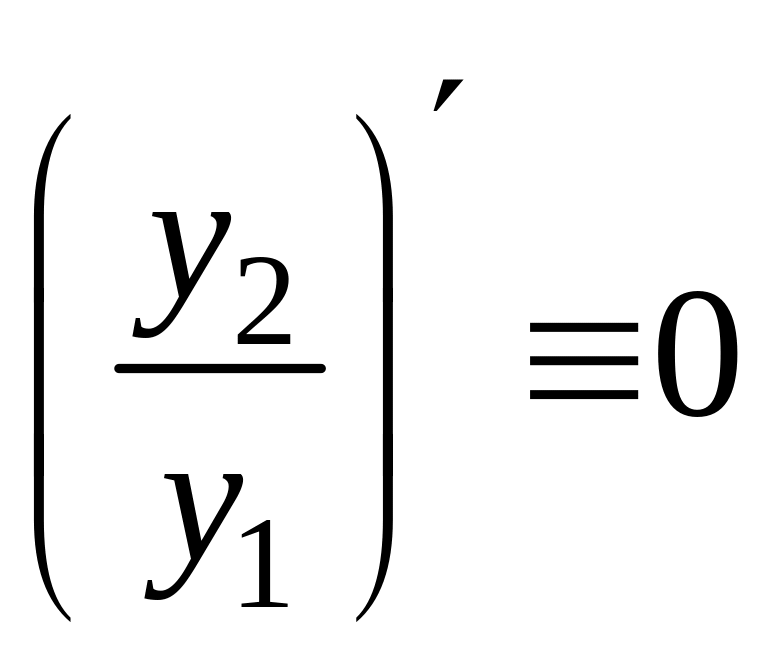Если .
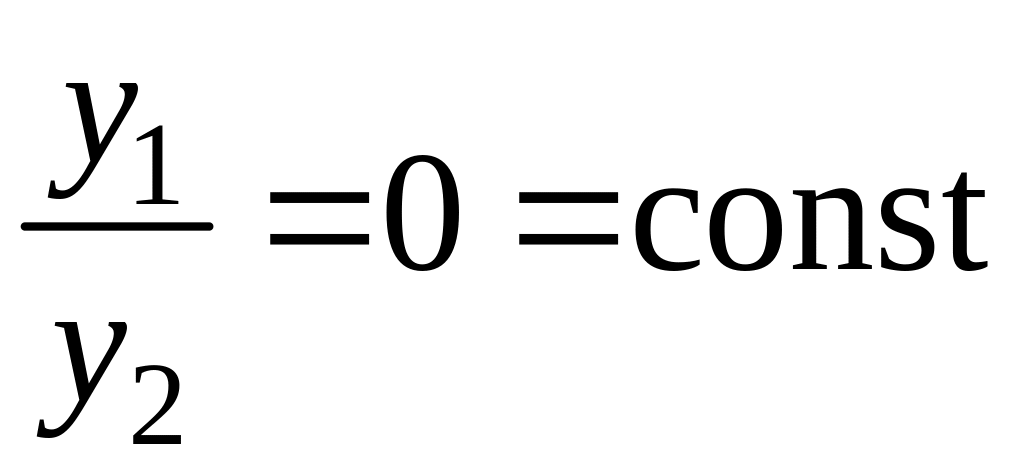