7.5.5. Д.У. В полных дифференциалах.

Уравнения вида:

, где называется д.у. в полных дифференциалах. Левая часть уравнения, в этом случае, есть полный дифференциал от некоторой функции U(x,y):

, т.к.

тогда - общий интеграл д.у.

Функция может быть найдена следующим образом:

, проинтегрируем его по x, считая y-фиксированным. Однако и , т.е.

(*)

Затем, из равенства

находим , подставив которую в (*), определим U(x,y).

Пример.

1. Убедимся, что это уравнение в полных дифференциалах:

2)

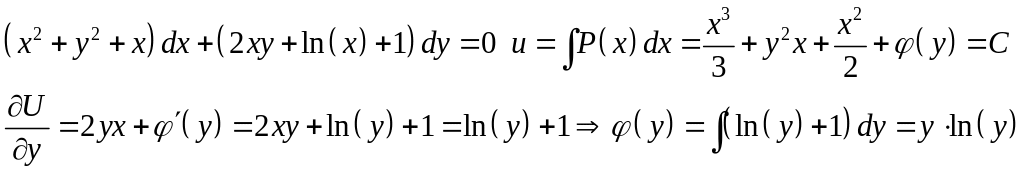
Д.у. 1-го порядка не разрешенные относительно

a) б)

Предполагается, что:

1. Они не могут быть разрешены относительно

2. Они не могут быть разрешены относительно x(a) или y(б), либо обе – 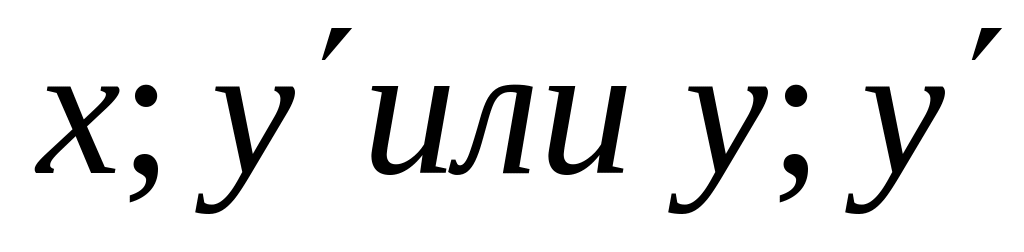- могут быть выражены через некоторый параметр “t”. Иными словами

) )

) )

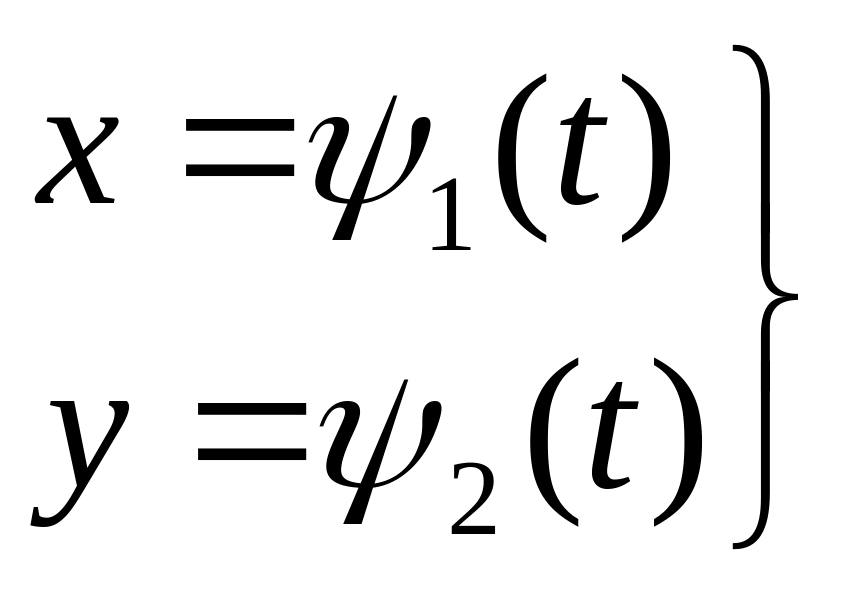
Причем в последних случаях:

Метод показывается на примерах:

1)

Обозначим , тогда , но ,

следовательно

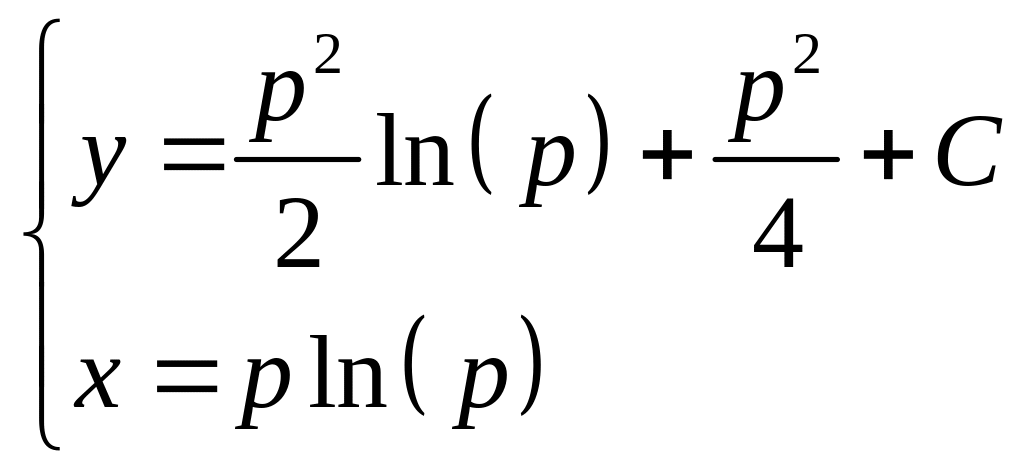
2) тогда , но

и т.д.

3. Д.у. 2-го порядка. Интегрирование методом понижения порядка.

3.1. Общие положения.

Д.у. 2-го порядка в общем случае имеет вид:

График всякого решения – интегральная кривая. Д.у. 2-го порядка устанавливает связь между x, y интегральной кривой, угловым коэффициентом касательной к этой кривой и ее производной

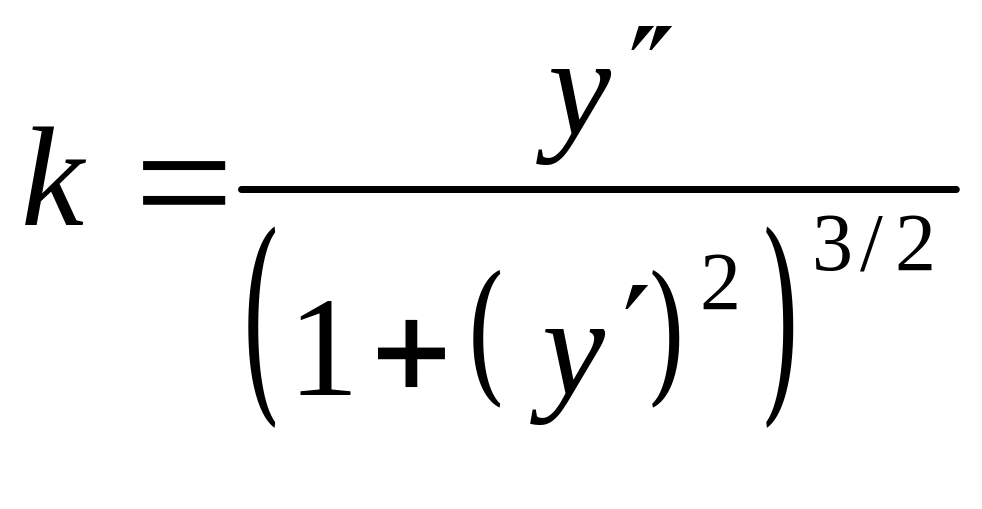
в этой же точке.

Проинтегрировать – найти вес решения.

Задача Коши: при

Теорема Коши.

Если в д.у. 2-го порядка, разрешенном относительно , т.е.

, - непрерывна во всей области , а ее частные производные

и - существуют и ограничены то для любого существует решение д.у. 2-го порядка, удовлетворяющее начальным условиям и такое решение единственное.

Решение задачи Коши – частное решение д.у. 2-го порядка.

Если менять , т.е. ……… , то любому при фиксированных будет соответствовать своя интегральная кривая. Получаем пучок, образующий однопараметрическое семейство . Одновременное изменение дает двухпараметрическое семейство:

Это семейство является общим решением д.у. 2-го порядка.

Опр. Общим решением д.у. 2-го порядка называют такое его решение, содержащее 2 произвольных константы, из которого выбором значений можно получить решение любой задачи Коши, поставленной для этого д.у. в области, где такое решение существует.

Отсюда следует, что для получения нужного решения задачи Коши следует

определить .

Пример.

, чтобы найти решение ……..

получим - частное решение.

3.2. Интегрирование простейших д.у. 2-го порядка.

К двум типам д.у. 2-го порядка : не содержащим явно неизвестную функцию или аргумент применяют метод понижения порядка:

1-й Тип: (*)

Введем

(**) - д.у. 1-го порядка относительно p.

Допустим, что (**) можно проинтегрировать и его общий интеграл

Заменяя в нем p на получим д.у. 1-го порядка относительно

Если и это д.у. можно проинтегрировать, то его общее решение

и будет решением (*).

При интегрировании (*) этим методом решение находят часто в виде или в параметрическом виде:

( Параметром может служить и )

Фактически данный метод сводится к интегрированию системы:

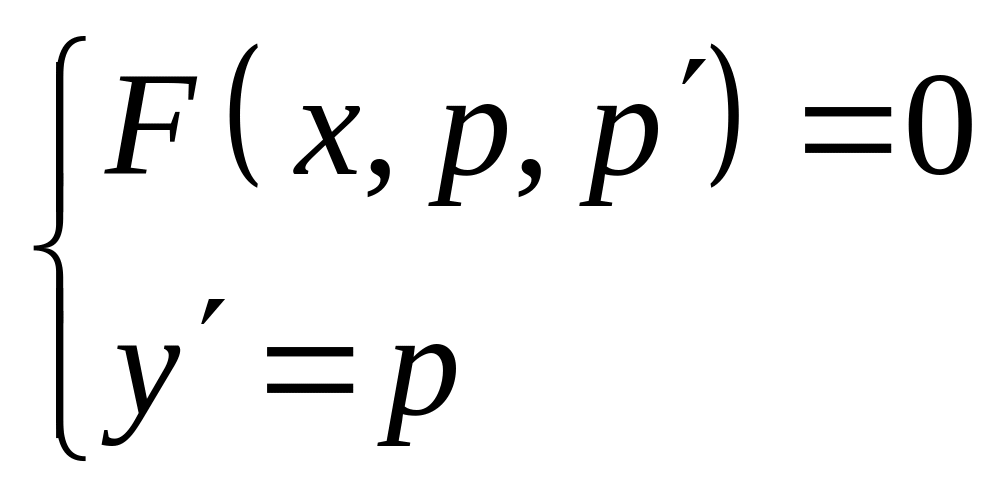
Примеры.

1)

     

Т.к. требуется найти только частное решение       

     

2) - с разделяющимися перемнными

2-й Тип: Введем новую переменную , а - за новую переменную. Тогда:

тогда

(***)

Допустим, что (***) проинтегрировано, тогда

или

- уравнение 1-го порядка.

Интегрируя последнее, получим:

- или общее решение

- общий интеграл

Либо в параметрической форме:

Примеры.

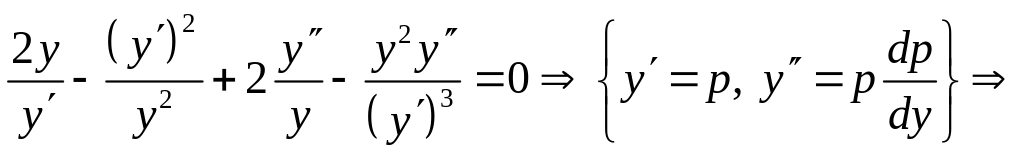
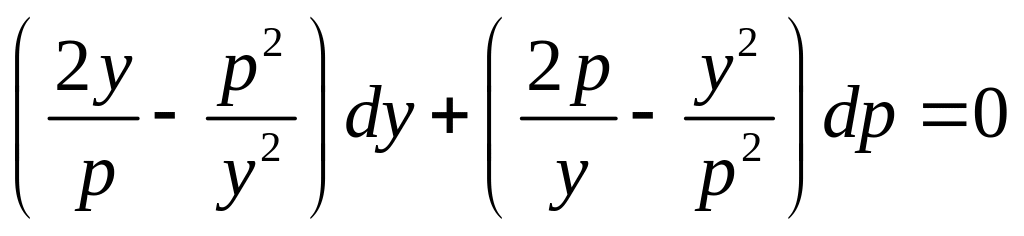- Это уравнение в полных дифференциалах.

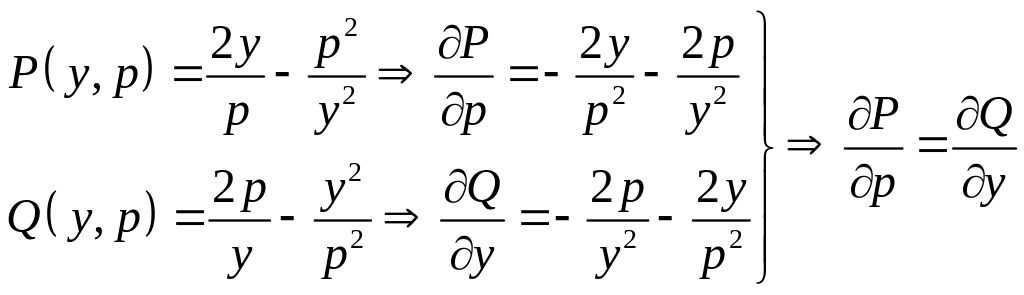
Интеграл тогда запишется следующим образом:

или т.к. , то получим :

(A)

Введем параметр следующим образом: подставляя в (А), получим:

и тогда

Дифференцируем y по t

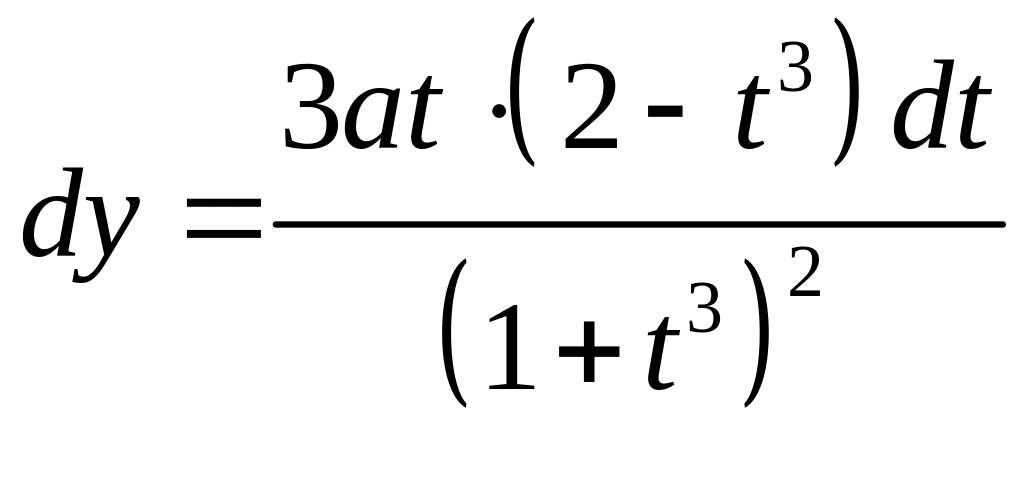
Но

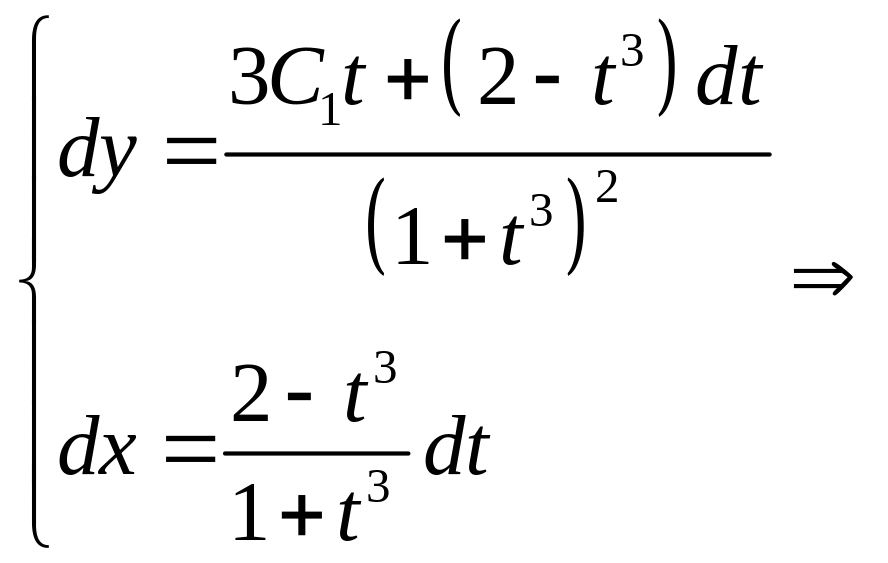
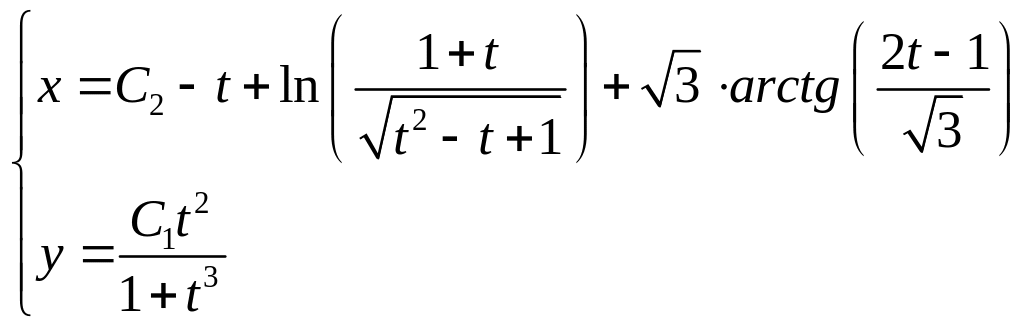
Пример 2. Проинтегрируем задачу Коши:

- уравнение с разделяющимися переменными.

- общий интеграл.

Определяем : или

или