Теорема про існування площини, яка проходите через три точки

Нам відомо два способи задання площини: площину можна провести через дві прямі, які перетинаються, а також через пряму і точку, яка не належить цій прямій. Існує третій спосіб.

Теорема.Через три точки, які не лежать на одній прямій, можна провести площину, і до того ж тільки одну.Слід звернути увагу учнів на те, що площина однозначно задається трьома точками, які не лежать на одній прямій, і тому в літературі площину, яка проходить через точки А, В, С і С АВ , позначають символом (АВС).

2. Зображення многогранників та методи побудови їх плоских перерізів.

Робота по ознайомленню учнів з проекційним кресленням може бути продовжена при навчанні рішення завдань на побудову перерізів многогранників.

Навчання рішенню завдань на побудову перерізів можна проводити в наступному плані. По-перше, початкове ознайомлення учнів з методами побудови перерізів необхідно проводити на метрично певних зображеннях. Зручно, наприклад, це виконати на зображенні куба і правильного тетраедра, супроводжуючи побудови на зображенні демонстрацією відповідних відносин на моделі. Все це буде сприяти зміцненню зв'язку зображення і оригіналу.

По-друге, точки, що визначають січну площину, слід задавати по можливості при різноманітному взаємне розташування цих крапок і багатогранника, перетин якого будується.

На рис.8 Наведено послідовність перших

таких завдань. Січна площину на цих кресленнях задається точками К (К1), М (М1) і Р (Р).

Рис. 8

При навчанні рішенню як цих завдань, так і будь-який з наступних учням слід виділяти окремі етапи рішення, що представляють собою відомі вже учням завдання на проекційному кресленні.

рис. 9(а,б)

Для побудови перерізу куба, представленого на рис. 9а, достатньо, наприклад, знайти точку перетину ребра СС1 з площиною КМР (К1М1 Р1). Метод побудови цієї точки зручно розкрити учням на прикладі рішення вже відомої їм завдання: на проекційному кресленні (рис. 9б) побудувати точку перетину площини β (β1) і проектує прямий СС1 На допоміжному кресленні слід лише по можливості точно відтворити взаємне розташування точок К (К1 ), M (M1), P (P1) і прямої СС1.

У порядку забезпечення наступності у вирішенні завдань на проекційному кресленні важливо підкреслити думку, що в якості допоміжної площини СС1КК1 могла б бути прийнята довільна площина, проведена через ребро СС1. Разом з тим учнів відразу слід привчати до раціонального вибору допоміжних площин.

При побудові перетини куба (мал. 10а) площиною КМР (К1М1Р1) не слід перешкоджати застосуванню загального методу (рис. 10б). Однак рішення цього завдання слід вести до тих пір, поки учні не здогадаються, що найбільш придатною допоміжної площиною буде площину межі BB1 CC, (рис. 10в), а не площині ВВ1ЕЕ1.

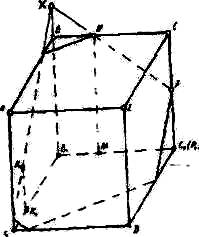рис. 10 (а, б, в)

Виділення січної площини - один з важливих етапів вирішення завдань на побудову перерізів.

При вирішенні задач на побудову перерізів в дохідливій формі вдається познайомити учнів з поняттями повного і метрично певного зображень, з рішенням позиційних і метричних задач.

Зображення багатогранників вводиться як метрично визначена відповідно до вищевикладеної методикою навчання побудови зображень. До поняття повного зображення можна підвести учнів, якщо домогтися від них розуміння, що зображення, побудоване за наперед заданим оригіналу, є в той же час зображення більш широкого класу фігур. Учні повинні розуміти, що зображення, наприклад, правильного тетраедра є разом з тим і зображенням всіх трикутних пірамід. Зображення правильної чотирикутної призми, висота якої в два рази більше сторони підстави, є в той же час і зображенням чотирикутних призм, в основі яких, лежить не тільки квадрат і висота яких не тільки в два рази більше сторони підстави, зображенням не тільки прямих призм, але і похилих.

Навичка в побудові перерізів доцільніше виробляти на повних зображеннях, не зв'язуючи себе без потреби з оригіналами наперед заданої форми. Це тим більш корисно, що на повних зображеннях розкриваються і деякі загальні властивості багатогранників.

3. Методичні особливості теми “Перпендикулярність прямих і площин”.

Зміст навчального матеріалу цієї теми можна розділити умовно на три блоки:

1) перпендикулярність прямих у просторі;

2) перпендикулярність прямої і площини;

3) перпендикулярність площин.

Методична схема вивчення кожного блоку та сама, що і в по­передній темі. Спочатку вводиться означення перпендикулярнос­ті відповідних об'єктів, потім формулюється і доводиться ознака їх перпендикулярності. Для прямої і площини розглядається за­дача на побудову перпендикулярних прямої і площини, доводяться єдиність такої площини та властивість перпендикулярної пря­мої і площини. Особливе місце і роль у цій темі належать навча­льному матеріалу, що стосується перпендикуляра і похилої до площини та теореми про три перпендикуляри. Остання застосо­вується при розв'язуванні задач, пов'язаних з многогранниками і тілами обертання. Схемою доведення цієї теореми часто послу­говуються в задачах.

Тому важливо домогтися того, щоб усі учні вміли доводити теорему про три перпендикуляри.

У зв'язку з вивченням перпендикулярності прямих у просторі треба повторити відповідний матеріал з планіметрії і стереомет­рії. У навчальній і методичній літературі відомі два види озна­чень перпендикулярних прямих у просторі:

1) дві прямі називаються перпендикулярними, якщо вони пе­ретинаються під прямим кутом;

2) дві прямі називаються взаємно перпендикулярними, якщо кути між ними дорівнюють 90°.

Друге означення охоплює і прямі, які не перетинаються, зок­рема мимобіжні прямі. Відповідно до цього прийнято і два види означень перпендикулярних прямої і площини:

1) пряма, що перетинає площину, називається перпендикуляр­ною до площини, якщо вона перпендикулярна до будь-якої прямої, яка лежить в даній площині і проходить через точку перетину;

2) пряма і площина називаються перпендикулярними, якщо пря­ма перпендикулярна до кожної прямої, яка лежить у площині.

Перевага першого означення для прямої і площини полягає в тому, що включення умови їх перетину в означення позбавляє не­обхідності спеціально доводити цей факт. Друге означення можна ввести в класах з поглибленим вивченням математики, доповнив­ши його умовою перетину прямої і площини (умова проходження прямої площини через точку перетину прямої і площини тут не вимагається). Таке означення полегшить доведення деяких теорем і розв'язування задач, зокрема теореми про три перпендикуляри.

Щодо означення перпендикулярних площин, то в учнів, за аналогією з означенням перпендикулярних прямих, виникає ба­жання означити їх як такі, що перетинаються під прямим кутом. Однак відразу ж виникає, проблема: що розуміти під кутом між площинами? У підручниках по-різному розв'язується ця пробле­ма. У підручнику О. В. Погорєлова дві площини, що пере­тинаються, називаються перпендикулярними, якщо третя площи­на, яка перпендикулярна до прямих перетину цих площин, пере­тинає їх по перпендикулярних прямих. У посібнику Л. С. Атанасяна та ін. спочатку вводиться означення двогранного кута, а відтак на цій основі дається означення перпендикулярних пло­щин.

Теореми, що стверджують ознаки перпендикулярності в прос­торі двох прямих, прямої і площини, двох площин, можна дово­дити різними способами. Здебільшого доведення виконуються шляхом розгляду паралелограмів і ланцюжка рівних трикутників. Разом з тим, наприклад, ознаку перпендикулярності прямої і пло­щини, теорему про два перпендикуляри і теорему про три пер­пендикуляри можна було б довести векторним методом.