В.2 Регулярные сигналы и их аналитическое описание. Ортогональные разложения функций

Широко известно использование аппарата Фурье для гармонического анализа детерминированных сигналов, при котором исходная функция разлагается в ряд по элементарным тригонометрическим функциям. Однако аппарат Фурье не является е Можно заданную в интервале времени 0-Т функцию (t) разлагать в ряд по любым другим функциям _k(t), принятым в качестве элементарных:

(1)

Сходимость этого ряда всегда обеспечивается. Задача разложения всегда сводится к выбору функций _k(t) и определению коэффициентов разложения C_k.

Коэффициенты C_k наиболее легко определяются, если функции _k(t) обладают свойством ортогональности. Функции называют ортогональными, если для них выполняется условие:

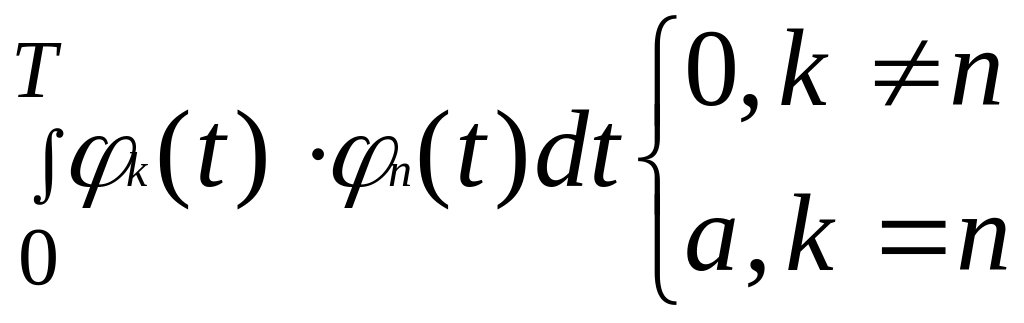(2)

Умножая левую и правую части уравнения (1) на _k(t) и интегрируя на интервале 0-Т, с учетом ортогональности получим

(3)

Второе условие, которым необходимо руководствоваться при выборе функций разложения, заключается в упрощении анализа при теоретических исследованиях.

Для точного воспроизведения функции при динственным.

представлении ее в виде ряда необходимо суммировать в общем случае бесконечное число членов. В некоторых случаях допустимо представление функций с некоторой погрешностью. При этом в разложении (1) можно ограничиться конечным числом членов:

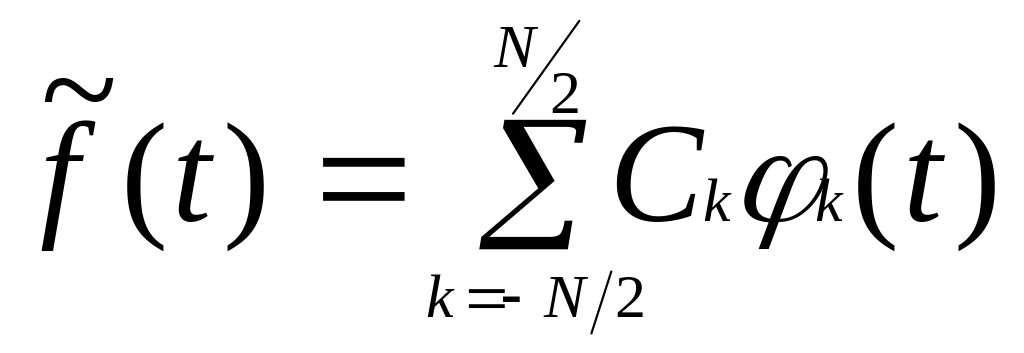(4)

Погрешность представления функции удобно оценивать величиной среднеквадратичной ошибки

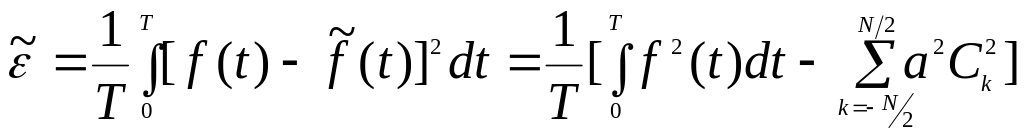(5)

При выборе функций разложения в этом случае необходимо руководствоваться условием обеспечения минимума ошибки при заданном числе членов ряда. При N величина среднеквадратичной ошибки стремится к нулю, так как

(6)

Последнее выражение аналогично равенству Парсеваля, используемому в аппарате Фурье.

Таким образом, всякую функцию можно с некоторой погрешностью представить в виде ряда с конечным числом членов. Представление непрерывного колебания в виде набора конечного числа функций или чисел называют иногда дискретизацией.

Возможность представления функции в виде конечного ряда позволяет осуществлять следующий способ передачи некоторого сигнала S(t). На передающем конце сигнала S(t) можно разложить в ряд по выбранным функциям _k(t) и передавать не сигнал, а лишь коэффициенты разложения C_k. На приемном конце, имея генераторы функций _k(t) по принятым коэффициентам можно восстановить переданный сигнал. Следовательно, с этой точки зрения в качестве функций разложения необходимо выбирать такие, которые легко генерировать.

Ниже рассматриваются два вида ортогональных разложений: разложение Фурье по гармоническим функциям и разложение Котельникова по функциям отсчетов.

Дискретизация функций рядами Фурье

Рассмотренное выше в п.1.1 представление сигналов в виде ряда Фурье является типичным примером ортогонального разложения. Семейство тригонометрических функций 1, Cos₀t, Sin₀t, Cos2₀t, Sin2₀t,..., Cosn₀t, Sinn₀t,...

является ортогональным на интервале 0T: (7)

где ₀=2/Т

Остановимся на некоторых особенностях использования рядов Фурье. Обычно в ряд Фурье принято разлагать периодические функции, а для непериодических функций использовать интеграл Фурье. Однако в теоретических исследованиях используют представление в виде ряда Фурье и не периодических сигналов. Такой переход от интеграла к ряду Фурье приводит к тому, что непериодическая функция длительностью Т вне заданного интервала периодически продолжается с периодом Т. Такая замена непериодической функцией периодической в общем случае не всегда допустима. Однако, в технике связи широко используются синхронные системы связи. Синхронная работа предполагает, что в месте приема известны начало и длительность сигнала, и, следовательно, возможна установка «нулевых начальных условий» в момент окончания сигнала. В этих условиях устраняется влияние периодического продолжения непериодического сигнала, и указанная замена при анализе прохождения сигналов через системы связи не приводит к ошибкам. Таким образом,

в указанных условиях любой сигнал можно охарактеризовать как непрерывным, так и дискретным спектром.

Для реальных сигналов связи спектр является быстро убывающей функцией частоты. Поэтому часто бывает возможным ограничиться конечным числом членов в ряде Фурье.

(8)

при достаточной точности представления сигнала. Если приемлемая точность обеспечивается при числе гармоник, равном N/2, то полоса частот, необходимая для передачи такого сигнала (без постоянной составляющей), равна

(9)

Если на приемлемой стороне имеются управляемые генераторы гармонических составляющих, то для восстановления сигнала необходимо передать

(10)

чисел, определяющих коэффициенты разложения.

Заметим, что для некоторых сигналов представленных в виде конечного ряда может быть точным, например для сигналов, составленных из N/2 гармоник или отрезка одного гармонического колебания, если длительность сигнала кратна периоду основной гармоники.

Величина В, равная удвоенному произведению длительности сигнала на ширину спектра частот, называется базой сигнала. Как известно из теории спектров, для наиболее часто встречающихся сигналов в виде отдельных импульсов произведение длительности на ширину спектра есть величина постоянная, имеющая порядок единицы t1. Для таких сигналов, называемых простыми или узкополосными, база равна 2.

В качестве сигналов можно использовать и такие, которые являются комбинациями простых сигналов (рис.В. 1).

S(t)

t

T₀ Т

S(t)

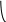
t

рис.В. 1

Эти комбинации представляют собой случайную последовательность простых сигналов. Такие сигналы называют составными или сложными. Для сложных сигналов ширина спектра будет такой же, что и для простых, а длительность и соответственно произведение 2_b будет больше. Сигналы, для которых база B=2_b1, называются широкополосными.

В заключении заметим, что представление сигналов в виде ряда Фурье весьма удобно при исследовании прохождения сигналов через различные линейные цепи. Ряд Фурье из всех возможных ортогональных разложений обеспечивает наименьшую погрешность представления при заданном числе членов разложения N. Однако ряд Фурье не удобен с реализационной точки зрения, так как операции гармонического анализа, а тем более синтеза технически осуществить довольно трудно.

Теорема Котельникова.

Любой сигнал с ограниченным спектром (бесконечный во времени) однозначно определяется своими отсчетами, взятыми через интервал времени т.е.

где U(k t) - аналоговая величина

Эта теорема утверждает, что если сигнал f(t) имеет преобразование Фурье Sf() отличное от нуля при частотах меньших 2Fm . То в отсчетах сигнала f(kt) взятых через интервал t=1/2Fm содержится вся информация о непрерывной функции f(t) . Из теоремы следует, что эти отсчеты содержат информацию о сигнале f(t) в любой момент времени. Однако частота отсчетов должна быть по крайней мере в два раза больше высшей частоты сигнала Fm .

Доказательство :

Дан сигнал F(t), его спектр:

Представим некоторую реализацию сигнала и его спектр:

f(t) S(f)

0 t 0 f

Если отсчеты сигнала брать с помощью бесконечноузких импульсов, расположенных в непосредственной близости друг от друга, мы однозначно определим любую функцию. Если интервал между импульсами увеличивать, то где-то мы начнем терять информацию о сигнале.

Рассмотрим случай, когда в качестве отсчетных импульсов используется периодическая последовательность импульсов длительностью , повторяемых через t=1/2Fm .

Временное и спектральное представление этих импульсов:

y(t)  S(f) t >> 

0 t f

t 0

Спектр отсчетных импульсов можно записать в виде ряда Фурье, т.е.

y(t)=A1cost+A2cost+A3cost+............

Процедуру взятия отсчетов удобно рассматривать как умножение функции f(t) на функцию y(t). Результирующий дискретизованный сигнал можно представить в виде суммы последовательностей импульсов, амплитуды которых равны значению функции f(t) в момент отсчета , а спектр такого сигнала представляет собой периодически повторяющуюся функцию Sf() с периодом , т.е.мы наблюдаем изменение амплитуды импульсов отсчета по закону f(t). И соответственно имеем на каждой гармонике спектра отсчетных импульсов спектр сигнала:

f(t)=f(t)y(t) f(f) 1/t-Fm 1/t+Fm

0 t 2t t -Fm 0 Fm 1/t 2/t f

Для восстановления первоначального сигнала нам достаточно отфильтровать полученный сигнал ФНЧ с частотой среза расположенной в интервале от Fm до 1/t-Fm .

Рассмотрим, какова может быть наименьшая частота следования отсчетных  импульсов, что бы еще имелась возможность отфильтровать полезный сигнал. В случае, если 1/t=2Fm мы еще имеем возможность отфильтровать полезный сигнал. Если же 1/t<2Fm, то произойдет наложение спектральных составляющих и восстановление первоначального сигнала без ошибки станет невозможным.

Следовательно, для восстановления сигнала, полученные отсчетные импульсы необходимо подать на вход ФНЧ с частотой среза равной Fm. Реакция идеального ФНЧ на узкий импульс единичной амплитуду представляет собой функцию вида:

На вход фильтра мы подаем сумму импульсов с амплитудами равными f(kt). Разложение сигнала f(t) в ряд Котельникова указывает на технический способ передачи непрерывной функции (сигнала) f(t) с ограниченным спектром путем передачи отсчетных импульсов, который сводиться к следующему: и со сдвигом один относительно другого на t=1/2Fm . Сигнал на выходе фильтра представляет собой сумму откликов, т.е.

Что соответствует ряду Котельникова.