3. Застосування лінійних диференціальних рівнянь до дослідження механічних та електричних коливань

[1], т.2,гл. ХІІІ, §§ 26-28

3.1. Дослідження коливань пружної підвіски культиватора

[1],т.2, гл. ХІІІ, § 26-28

Рівняння, яке описує пружну підвіску культиватора (рис.1) має вигляд

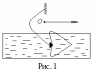
, (3.1)

де

– маса ґрунту на лапі культиватора;

– маси стійки лапи культиватора;

– маса лапи культиватора;

– жорсткість лапи культиватора;

– реакція ґрунту на лапу культиватора.

Рівняння (3.1) є математичною моделлю коливань пружної підвіски культиватора.

Величини , та визначаються експериментально для конкретного культиватора.

Розв’язок рівняння (3.1) визначає закон коливань пружної підвіски культиватора. Для однозначного визначення закону коливань, необхідні початкові умови

; (3.2)

Рівняння (3.1) зручно записати у вигляді

(3.3)

Загальний розв’язок цього рівняння ,

де – загальний розв’язок відповідного однорідного рівняння

, (3.4)

яке описує вільні коливання, без наявності зовнішніх сил, а – частинний розв’язок неоднорідного рівняння (3.3).

Загальний розв’язок однорідного рівняння (3.4) має вигляд

, (3.5)

де – частота власних коливань підвіски культиватора.

Для знаходження необхідно знайти вигляд функції . В реальних умовах реакція ґрунту на лапу культиватора має періодичний характер і тому описується періодичною функцією, наприклад

,

де – частота збурної сили.

При знаходженні , згідно теорії, можуть бути два випадки:

1) – частота власних коливань не співпадає з частотою вимушеної сили, тоді

(3.6)

Підставляючи в рівняння (3.3) при умові, що , та порівнюючи коефіцієнти зліва і справа при функціях та , одержимо

; ;

Отже, загальний розв’язок має вигляд

(3.7)

Підставляючи початкові умови (3.2) в загальний розв’язок (3.7), матимемо

(3.8) Ми бачимо, що якщо частота власних коливань дуже близька до частоти вимушеної

сили , то величина є дуже мала, а амплітуда буде дуже велика, що небажано для культиватора. Щоб уникнути такого випадку, потрібно змінити

, тобто змінити жорсткість , або масу , або її складові.

2) , тобто частота власних коливань співпадає з частотою вимушеної сили, тоді згідно теорії, треба шукати у вигляді

(3.9)

Підставляючи в (3.3) та порівнюючи коефіцієнти при однакових функціях, матимемо

; ;

Загальний розв’язок має вигляд

(3.10)

Третій доданок в (3.10) вказує на те, що амплітуда згодом зросте і настане, як в даному випадку, не бажане явище – резонанс. У випадку виникнення резонансу, необхідно також порушити умову , тобто змінити маси або , або змінити жорсткість лапи культиватора.

3.2. Застосування лінійних диференціальних рівнянь до дослідження електричних коливань

[1], глава ХІХ, §§ 1-6, 8-12, 14-18

Для електричного кола (рис.2), яке складається із послідовно сполучених опору , котушки індуктивності , ємності та даної прикладної напруги треба визначити струм , який буде у колі після підключення його до джерела напруги. За законом Кірхгофа електрична сила в колі дорівнює сумі падіння напруги на активному опорі , котушці індуктивності та ємності , тобто

,

де ; ;

тоді

Диференціюючи по

або . (3.11)

Лінійне диференціальне рівняння (3.11) є математичною моделлю кола . Його розв’язок і дає закон зміни струму з часом. Щоб розв’язок однозначно визначав закон зміни струму з часом необхідні початкові умови.

, (3.12)

Якщо , а , то рівняння (3.11) матиме вигляд

(3.13)

Загальний розв’язок рівняння (3.13)

де – загальний розв’язок відповідного однорідного рівняння

(3.14)

яке описує вільні (власні) коливання, що будуть спостерігатися у колі, а

– частинний розв’язок неоднорідного рівняння (3.13).

Загальний розв’язок рівняння (3.14), згідно теорії, має вигляд

(3.15)

де ; ;

При знаходженні , згідно теорії, мають місце два випадки:

1) , частота власних коливань не співпадає з частотою прикладеної напруги, тоді

(3.16)

Підставляючи у рівняння (3.13) та порівнюючи коефіцієнти при функціях та , матимемо

; ;

(3.17)

Отже, загальний розв’язок рівняння (3.13) буде

(3.18)

З (3.18) видно, що струм у колі буде складатися з суми двох коливань, власних коливань з частотою та вимушених з частотою . Сталі A та знаходяться з початкових умов (3.12). Якщо різниця буде дуже мала, то амплітуда у другому доданку (3.18) буде велика, хоч і обмежена. Це дає змогу створювати коливання з великою амплітудою, що застосовується в різного роду підсилюючих пристроях.

2) , тобто частота власних коливань співпадає з частотою прикладеної напруги, тобто, згідно теорії, потрібно шукати у вигляді

(3.19)

Підставляючи (3.19) у (3.13) і порівнюючи коефіцієнти при функціях та , матимемо

; M = 0

, (3.20)

а загальний розв’язок буде

(3.21)

Другий доданок у (3.21) показує, що з часом амплітуда зростає і наступає явище резонансу. У випадку не бажаного виникнення резонансу необхідно порушити умову , тобто змінити параметри кола або .

Частинний розв’язок рівняння

(3.22)

який задовольняє початковим умовам (3.12) можна знайти і операторним методом.

Якщо оригіналу відповідає зображення , тобто

; ;

;

;

то диференціальному рівнянню (3.22), з початковими умовами (3.12), відповідає операторне рівняння відносно

(3.23)

Розв’яжемо рівняння (3.23) відносно I(p), одержимо операторний розв'язок

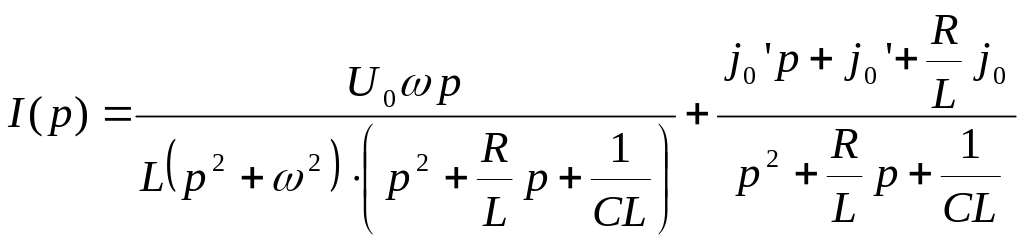(3.24)

Розкладаючи праву частину (3.24) на суму елементарних дробів або застосовуючи формули розкладання, за зображенням знайдемо оригінал , який є частинним розв’язком диференціального рівняння (3.22), що задовольняє початковим умовам (3.12).

П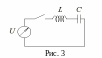 риклад 11. Для електричного кола, яке складається з послідовно з’єднаних котушки індуктивності Гн, ємності Ф та заданої прикладеної напруги (рис.3), скласти диференціальне рівняння та визначити струм j(t), який буде спостерігатися в колі після підключення його до джерела навантаження, класичним та операторним методами, якщо

, .

Розв’язання. За законом Кірхгофа

Диференціюючи по

або (1)

1. Знайдемо частинний розв’язок рівняння (1), який задовольняє початковим умовам

, (2)

класичним способом. Загальний розв’язок ,

де – загальний розв’язок відповідного однорідного рівняння

(3)

– частинний розв’язок неоднорідного рівняння (1).

Складемо характеристичне рівняння ,

Тоді (4)

Складемо вигляд , за правою частиною рівняння (1), оскільки число співпадає з коренем характеристичного рівняння, то частинний розв’язок будемо шукати у вигляді

(5)

	4
+	0
	1

Для визначення коефіцієнтів A та B застосуємо метод невизначених коефіцієнтів. Підставимо розв'язок (5) у рівняння (1) і прирівнюємо коефіцієнти зліва та справа при однакових функціях

sin2t	– 4A = 0,	A = 0
cos2t	4B = 4,	B = 1.

Тоді = t sin2t. (6)

Загальний розв’язок буде

Сталі та знайдемо з початкових умов (2)

тоді

2. Знайдемо струм операторним методом. Складемо операторне рівняння.

Нехай ;

;

;

Тоді

Знайдемо операторний розв’язок

За формулами 15 та 12 таблиці (додаток 1) знайдемо

.