- •Мелітополь
- •3. Застосування лінійних диференціальних рівнянь до
- •1. Диференціальні рівняння першого порядку
- •1.1. Диференціальні рівняння з відокремлюваними змінними
- •1.2. Однорідні диференціальні рівняння
- •1.3. Лінійні диференціальні рівняння та рівняння я. Бернуллі
- •2. Диференціальні рівняння другого порядку
- •2.1. Диференціальні рівняння другого порядку, які допускають пониження порядку
- •2.2. Лінійні диференціальні рівняння другого порядку зі сталими коефіцієнтами
- •3. Застосування лінійних диференціальних рівнянь до дослідження механічних та електричних коливань
- •3.1. Дослідження коливань пружної підвіски культиватора
- •3.2. Застосування лінійних диференціальних рівнянь до дослідження електричних коливань
- •3.3. Модель ринку з прогнозованими цінами
- •Розділ 2. Завдання для індивідуальної роботи Теоретичні питання
- •Розрахункові завдання
- •1. Знайти розв’язок задачі Коші
- •Література
- •Міністерство аграрної політики україни
- •Таврійський державний агротехнологічний університет
- •Кафедра вищої математики
- •Диференціальні рівняння
2. Диференціальні рівняння другого порядку
[1], глава ХІІІ, § 16
2.1. Диференціальні рівняння другого порядку, які допускають пониження порядку
[1], глава ХІІІ, §§ 17-18
Диференціальні рівняння другого порядку, що не містять явно у собі змінні або , за допомогою належної заміни змінної допускають зниження порядку та інтегруються до кінця.
Якщо
диференціальне рівняння другого порядку
явно не містить
,
то застосовується підстановка
![]() ,
,
![]() ,
якщо вона явно не містить
,
то
,
якщо вона явно не містить
,
то
;
![]() .
.
Приклад 7. Знайти розв’язок задачі Коші
![]() ;
; ![]() ;
; ![]()
Розв’язання.
Оскільки диференціальне рівняння явно
не містить y,
то застосуємо підстановку
![]() ;
тоді одержимо
;
тоді одержимо
![]() або
або ![]() .
.
Це лінійне рівняння першого порядку, загальний розв’язок якого знайдемо, наприклад, за методом І. Бернуллі.
Загальний
розв’язок відшукаємо у вигляді
![]()
![]()
тоді ![]() або
або ![]() ;
;
![]() ;
; ![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
,
![]()
Знайдемо
сталу С1
із початкової умови
![]() .
Оскільки
.
Оскільки
![]() то
то
![]() ;
; ![]() ;
; ![]() .
.
Тоді
![]() ,
але
,
але
![]() .
.
І знову одержимо диференціальне рівняння першого порядку
![]() ;
; ![]() ;
;
![]() ;
; ![]()
![]() знайдемо
із початкової умови
.
знайдемо
із початкової умови
.
![]() ;
; ![]() ;
; ![]() – розв’язок задачі Коші.
– розв’язок задачі Коші.
Приклад 8. Знайти розв’язок задачі Коші
![]() ;
; ![]() ;
; ![]()
Розв’язання. Оскільки рівняння явно не містить , то застосуємо заміну
;
тоді ![]()
![]() ; P
=
0; y'
=
0; y
= C.
; P
=
0; y'
=
0; y
= C.
З
урахуванням початкової умови y
=
0.
![]() – це диференціальне рівняння з
відокремлюючими змінними.
– це диференціальне рівняння з
відокремлюючими змінними.
![]() ;
; ![]() ;
; ![]()
![]() ;
; ![]()
Знайдемо С1 із початкових умов та
Оскільки
![]() ,
то
,
то
![]() ;
;
![]() ;
;
![]() .
.
Замінимо
![]() на
на
![]() ,
знову одержимо диференціальне рівняння
першого порядку з відокремлюючими
змінними
,
знову одержимо диференціальне рівняння
першого порядку з відокремлюючими
змінними
![]() ;
; ![]() ;
; ![]()
![]()
Знайдемо
із початкової умови
,
звідки
![]() .
.
Тоді
![]() – частинний інтеграл задачі Коші.
– частинний інтеграл задачі Коші.
2.2. Лінійні диференціальні рівняння другого порядку зі сталими коефіцієнтами
[1], глава ХІІІ, §§ 20-24
Лінійне диференціальне рівняння другого порядку зі сталими коефіцієнтами має вигляд
![]() , (2.1)
, (2.1)
де
![]() – сталі числа, а
– сталі числа, а
![]() – відома функція.
– відома функція.
Якщо
![]() ,
то диференціальне рівняння
,
то диференціальне рівняння
![]() (2.2)
(2.2)
зветься лінійним однорідним, а рівняння (2.1) – лінійним неоднорідним.
Загальний розв'язок однорідного рівняння (2.2) подається у вигляді
![]() (2.3)
(2.3)
де
![]() та
та
![]() – фундаментальна система (лінійно
незалежні частинні розв'язки рівняння
(2.2));
– фундаментальна система (лінійно
незалежні частинні розв'язки рівняння
(2.2));
![]() та
– довільні сталі.
та
– довільні сталі.
Частинні розв’язки залежать від коренів характеристичного рівняння
![]() .
.
Якщо :
характеристичне рівняння має дійсні і різні корені
![]() ;
; ![]() ;
; ![]() ,
,
то загальний розв’язок
![]() ;
;
характеристичне рівняння має дійсні і рівні корені
![]() ;
;
;
; ![]() ,
,
то загальний розв’язок
![]() ;
;
характеристичне рівняння має комплексно-спряжені корені
![]() ;
; ![]() ;
;
тоді
![]() ;
; ![]() ,
а загальний розв’язок
,
а загальний розв’язок
![]()
Загальний
розв’язок лінійного неоднорідного
рівняння (2.1) складається із суми двох
розв’язків
![]() ,
,
де ![]() – загальний розв’язок відповідного
однорідного рівняння (2.2)
– загальний розв’язок відповідного
однорідного рівняння (2.2)
![]() – будь-який частинний розв’язок
неоднорідного рівняння (2.1)
– будь-який частинний розв’язок
неоднорідного рівняння (2.1)
Якщо права частина рівняння (2.1) має вигляд
![]() ,
,
де
![]() – многочлен степені n,
а m –
стале число, тоді:
– многочлен степені n,
а m –
стале число, тоді:
якщо число m не співпадає з коренями характеристичного рівняння тоді
![]() ;
;
де Qn(x) – многочлен того ж степеня, що і , тільки з невизначеними коефіцієнтами;
якщо число m співпадає з одним із коренів характеристичного рівняння, тоді
![]() ;
;
якщо число
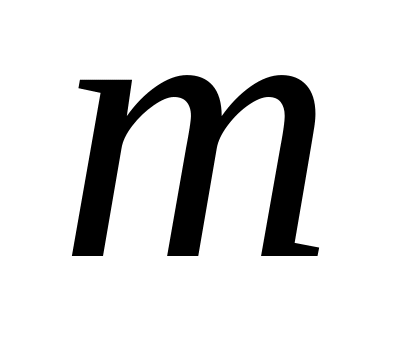 співпадає з коренями характеристичного
рівняння
співпадає з коренями характеристичного
рівняння
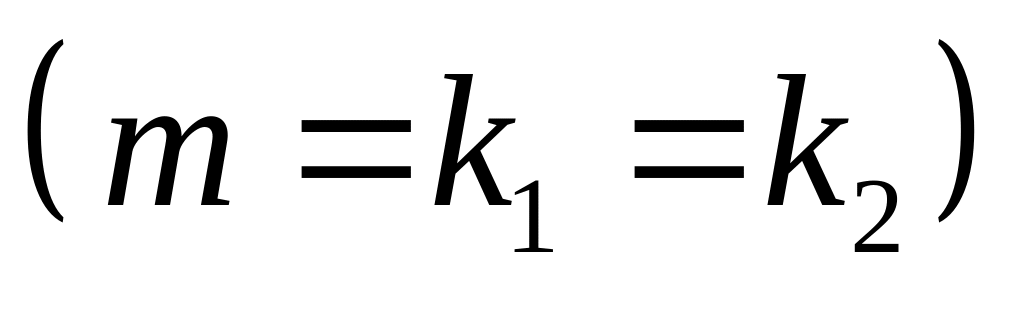 ,
тоді
,
тоді
![]() ;
;
коефіцієнти
многочлена
![]() знаходяться за методом невизначених
коефіцієнтів.
знаходяться за методом невизначених
коефіцієнтів.
Якщо права частина рівняння (2.1) має вигляд
![]() ;
; ![]() ;
;
де та – многочлени, тоді :
1) якщо
число
![]() не співпадає з коренем характеристичного
рівняння, тоді
не співпадає з коренем характеристичного
рівняння, тоді
![]()
де
![]() та
та
![]() – многочлени степеня n
з невизначеними коефіцієнтами;
– многочлени степеня n
з невизначеними коефіцієнтами;
2) якщо число співпадає з коренем характеристичного рівняння, тоді
![]() .
.
Коефіцієнти многочленів та також знаходяться за методом невизначених коефіцієнтів (додаток 2).
Приклад 9. Знайти загальний розв’язок рівняння
![]()
Розв’язання. За теоремою про структуру загального розв’язку неоднорідного диференціального рівняння 2-го порядку зі сталими коефіцієнтами маємо
![]() ,
,
де ![]() – загальний розв’язок однорідного
рівняння;
– загальний розв’язок однорідного
рівняння;
![]() – частинний розв’язок усього рівняння.
– частинний розв’язок усього рівняння.
Знайдемо спочатку загальний розв’язок відповідного однорідного рівняння
![]()
Складемо
характеристичне рівняння
![]() ,
та знайдемо його корені
,
та знайдемо його корені
![]() ,
,
![]() .
Тоді загальний розв’язок однорідного
рівняння буде
.
Тоді загальний розв’язок однорідного
рівняння буде
![]()
Знайдемо
тепер частинний розв’язок неоднорідного
рівняння. Оскільки число
![]() і не співпадає з коренями характеристичного
рівняння, тоді
і не співпадає з коренями характеристичного
рівняння, тоді
|
2 |
|
+ |
–3 |
|
|
1 |
|
|
|
|
Скоротивши
на
![]() і приводячи подібні отримаємо
і приводячи подібні отримаємо
![]()
(Обчисливши
![]() та
та
![]() і підставивши їх значення
в неоднорідне рівняння знайдемо
коефіцієнти методом невизначених
коефіцієнтів). Прирівнявши коефіцієнти
зліва та справа при однакових степенях
x,
матимемо систему
і підставивши їх значення
в неоднорідне рівняння знайдемо
коефіцієнти методом невизначених
коефіцієнтів). Прирівнявши коефіцієнти
зліва та справа при однакових степенях
x,
матимемо систему
Тоді
![]() ,
а загальний розв’язок
,
а загальний розв’язок
![]()
Приклад 10. Знайти загальний розв’язок рівняння
![]() .
.
Розв’язання. Загальний розв’язок неоднорідного диференціального рівняння дорівнює
.
Знайдемо спочатку загальний розв’язок відповідного однорідного рівняння
![]() .
.
Складемо характеристичне рівняння
![]() ,
, ![]() ,
, ![]() тоді
тоді
![]()
Знайдемо
тепер частинний розв’язок
неоднорідного рівняння.
Оскільки число
![]() і співпадає з коренем характеристичного
рівняння, тоді
і співпадає з коренем характеристичного
рівняння, тоді
|
4 |
|
+ |
0 |
|
|
1 |
|
|
|
|
Коефіцієнти
![]() і
і
![]() знайдемо методом
невизначених коефіцієнтів. Прирівнявши
зліва і справа коефіцієнти при функціях
знайдемо методом
невизначених коефіцієнтів. Прирівнявши
зліва і справа коефіцієнти при функціях
![]() та
та
![]() матимемо
матимемо
-
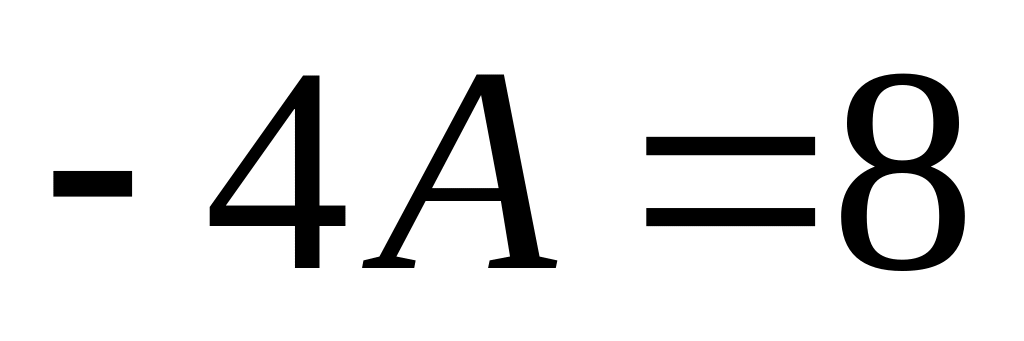 ;
;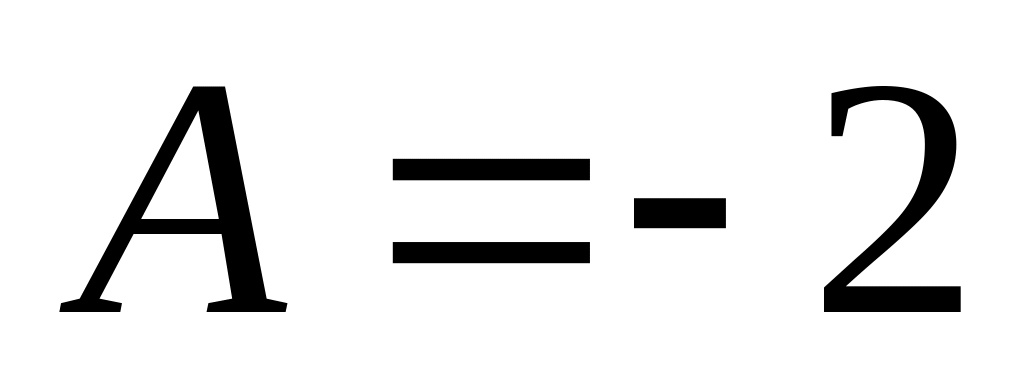
 ;
;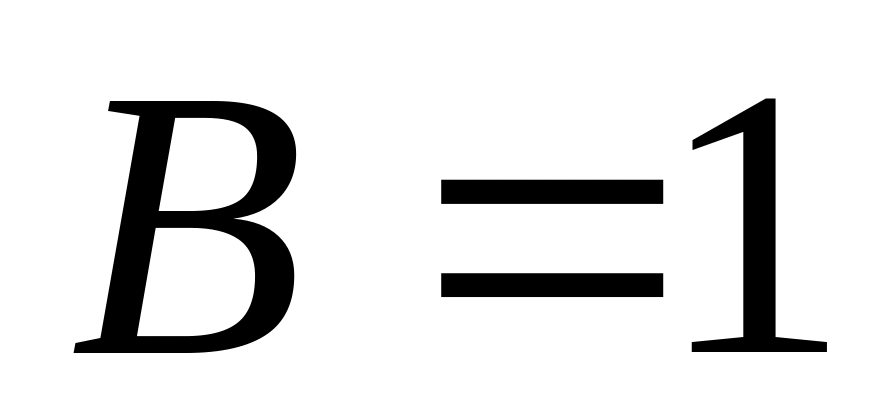
Тоді
![]() ,
а загальний розв’язок
,
а загальний розв’язок
![]() .
.