
- •Раздел 11. Элементы математической статистики
- •11.1 Вариационный ряд и его статистические характеристики.
- •Статистическое распределение выборки
- •Геометрическое представление
- •Выборочные характеристики статистического распределения
- •Задачи для самостоятельного решения:
- •Контрольные вопросы:
- •11.2 Статистические оценки параметров распределения
- •11.3 Статистические методы обработки экспериментальных данных
- •Проверка гипотезы о соответствии эмпирического распределения нормальному закону
- •Отбрасывание «выскакивающих» вариант
- •Сравнение средних арифметических и дисперсий двух вариационных рядов
- •Регрессионный и корреляционный анализ
- •Задачи для самостоятельного решения
- •Контрольные вопросы
11.3 Статистические методы обработки экспериментальных данных
Можно выделить следующие задачи статистического анализа:
По данным выборки дать описание генеральной совокупности, построив доверительные интервалы для параметров распределения.
Определить значимость различия между двумя совокупностями (чаще всего сравнивают опыт с контролем).
Изучить статистическую связь между двумя совокупностями (регрессионный и корреляционный анализ).
Решению любой из этих задач предшествует общая процедура, включающая этапы:
а) Упорядочение эмпирической совокупности. Представление вариационного ряда;
б) Выбор математической модели распределения;
в) Отбрасывание «выскакивающих» вариант (или оценка грубых ошибок).
Процедура построения вариационного ряда подробно рассмотрена в разделе 11.1. Остановимся на процедуре выбора математической модели распределения, ее же можно отнести к задаче проверки гипотез.
Проверка гипотезы о соответствии эмпирического распределения нормальному закону
Рассмотрим один из наиболее распространенных
критериев – критерий
![]() (К.Пирсона)
применительно к нормальному закону с
плотностью распределения:
(К.Пирсона)
применительно к нормальному закону с
плотностью распределения:
![]() .
.
В соответствии с этим критерием, меру
близости эмпирического распределения
к теоретическому (нормальному закону),
с параметрами
![]() и
и
![]() ,
оценивают по величине:
,
оценивают по величине:
![]() ,
где:
,
где:
mi - частоты эмпирического распределения,
npi - частоты предполагаемого теоретического (нормального) распределения;
![]() - число интервалов разбиения в эмпирическом
распределении.
- число интервалов разбиения в эмпирическом
распределении.
Полученное расчетное значение
![]() сравнивают с теоретическим, табличным
значением
сравнивают с теоретическим, табличным
значением
![]() (
(![]() – уровень значимости,
– уровень значимости,
![]() – число степеней свободы, в данном
случае
– число степеней свободы, в данном
случае
![]() .
В случае
.
В случае
![]() ,
нулевая гипотеза Н0 о совпадении
эмпирического распределения с
теоретическим принимается, в противном
случае, если
,
нулевая гипотеза Н0 о совпадении
эмпирического распределения с
теоретическим принимается, в противном
случае, если
![]() ,
гипотеза отвергается, нельзя считать,
что эмпирическое распределение
соответствует теоретическому –
нормальному закону распределения.
,
гипотеза отвергается, нельзя считать,
что эмпирическое распределение
соответствует теоретическому –
нормальному закону распределения.
Замечания: 1) Критерием
![]() можно пользоваться только при достаточно
большом числе вариант (
можно пользоваться только при достаточно
большом числе вариант (![]() ).
).
2) Число степеней свободы v равно разности между значением числа независимых величин, использованных при вычислении этой статистики (в данном случае k), и числом уравнений связи, которых, в случае нормального распределения, три:
![]() ;
;
![]() ;
;
![]() .
.
Эти уравнения связи определяют те
значения характеристик
![]() ,
по которым строилось теоретическое
нормальное распределение.
,
по которым строилось теоретическое
нормальное распределение.
Пример 1. Сравним эмпирическое распределение содержания воды в тканях (см. п.11.1 пример 3) с теоретическим нормальным законом.
Расчеты проводятся по схеме:
Строится интервальный вариационный ряд и вычисляются его выборочные характеристики (см. п.11.1 пример 3).
Находятся новые границы интервалов zi в долях S относительно
 по формуле:
по формуле:
![]() (
(![]() ).
).
При этом начало нового интервала и конец
последнего принимаются, соответственно,
![]() ;
;
![]() .
.
Для каждого zi (
 )
находим значения интегральной функции
Лапласа
)
находим значения интегральной функции
Лапласа
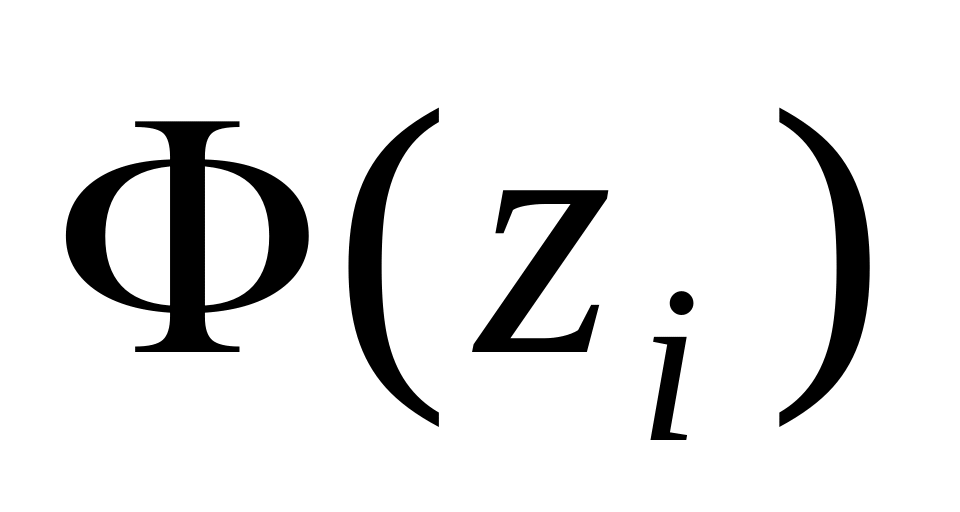 по соответствующей таблице.
по соответствующей таблице.Для каждого интервала определяем:
а) Теоретическую вероятность
![]() .
.
б) Теоретические частоты
![]() (п – объем выборки).
(п – объем выборки).
в) Квадрат разности эмпирической и
теоретической частот
![]() .
.
г) Отношение
![]() .
.
5) Рассчитываем сумму:
![]() .
.
Для нашего примера расчеты по указанной схеме приведены в следующей таблице:
№ интер-вала |
Границы интервалов (ai-1,ai) |
mi |
Границы интервалов (zi-1,zi) |
|
|
|
|
|
1. |
(87.25,87.75) |
4 |
( |
-0.500 |
0.122 |
6.1 |
4.41 |
0.72 |
2. |
(87.75,88.25) |
11 |
(-1.165,-0.640) |
-0.378 |
0.1391 |
6.96 |
16.22 |
2.32 |
3. |
(88.25,88.75) |
11 |
(-0.64,-0.12) |
-0.2389 |
0.1911 |
9.16 |
3.38 |
0.37 |
4. |
(88.75,89.25) |
10 |
(-0.120,0.408) |
-0.0478 |
0.2048 |
10.24 |
0.058 |
0.00 |
5. |
(89.25,89.75) |
6 |
(0.408,0.934) |
0.1570 |
0.1670 |
8.34 |
5.47 |
0.67 |
6. |
(89.75,90.25) |
3 |
(0.934,1.470) |
0.3240 |
0.1052 |
5.26 |
5.11 |
0.97 |
7. |
(90.25,90.75) |
3 |
(1.470,2.000) |
0.4292 |
0.0480 |
2.40 |
0.36 |
0.15 |
8. |
(90.75,91.25) |
0 |
(2.000,2.500) |
0.4772 |
0.0165 |
0.82 |
0.67 |
0.65 |
9. |
(91.25,91.75) |
2 |
(2.500,
|
0.4937 |
0.0063 |
0.32 |
2.82 |
|
СУММА |
50 |
|
|
1.000 |
50.00 |
|
5.85 |
|
В таблице два последних интервала
объединены, границы объединенного
интервала в z
![]() ,
эмпирическая частота в нем равна 2, а
теоретическая – 1,14. Объединение крайних
интервалов рекомендуется в случаях,
когда имеются «пустые» интервалы. Сумма
значений по последнему столбцу
характеризует расчетное значение
критерия
,
эмпирическая частота в нем равна 2, а
теоретическая – 1,14. Объединение крайних
интервалов рекомендуется в случаях,
когда имеются «пустые» интервалы. Сумма
значений по последнему столбцу
характеризует расчетное значение
критерия
![]() .
Число степеней свободы, с учетом
объединения интервалов, равно 8 – 3 = 5.
.
Число степеней свободы, с учетом
объединения интервалов, равно 8 – 3 = 5.
В таблице 5 приложения находим – в
строке, соответствующей степени свободы
5, первое значение, большее
![]() и соответствующее ему
и соответствующее ему
![]() Значению
Значению
![]() соответствует
соответствует
![]() Значит, с вероятностью 1 – 0.2 = 0.8 (или с
надежностью 80%) можно считать, что
исследуемое эмпирическое распределение
совпадает с теоретическим нормальным
законом
Значит, с вероятностью 1 – 0.2 = 0.8 (или с
надежностью 80%) можно считать, что
исследуемое эмпирическое распределение
совпадает с теоретическим нормальным
законом
