
Линеаризация уравнений динамики
Достаточно часто встречаются звенья, имеющие нелинейную зависимость между входной и выходной координатами. Если для малых отклонений от установившегося режима нелинейность несущественна, то в этом случае до составления исходных дифференциальных уравнений САУ выполняют процедуру линеаризации.
Линеаризацией называется замена реальных нелинейных уравнений статических характеристик элементов близкими к ним линейными уравнениями. Линеаризация возможна, если нелинейная характеристика непрерывна и имеет непрерывные частные производные. На рис.2.2 приведена геометрическая интерпретация линеаризации по методу малых отклонений.
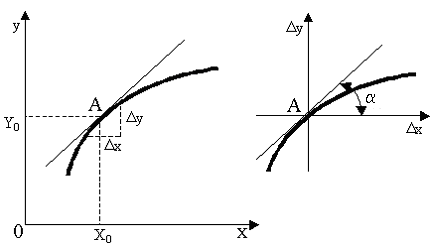
Рис.2.2. Геометрическая интерпретация линеаризации
Разложив функцию y=f(x) в ряд Тейлора, получим
![]() ,
,
где y0 – значение выхода, соответствующее входу x0; dky/dxk – значения производных, взятых в точке А(x0;y0). Тогда для малых отклонений x:
![]()
![]() или
или
![]() ,
,
где
![]() при x=x0.
при x=x0.
Если выходная величина элемента зависит от нескольких входных воздействий, то при линеаризации по методу малых приращений следует определять частные производные по всем воздействиям, а приращение выхода является суммой частных приращений, т.е.
![]() ,
,
где
x1,
x2,
…,xn
– приращения входных воздействий;
![]() - частные производные.
- частные производные.
П р и м е р. Линеаризовать уравнение характеристики элемента умножения y=x1x2 в точке y0=x01x02.
Р е ш е н и е. В соответствии с малыми приращениями
y0+y=(x01+x1) (x02+x2)= x01x02+x01x2+x02x1+x1x2=
=y0+x01x2+x02x1+x1x2 y0+x01x2+x02x1,
пренебрегая малыми высшего порядка.
Тогда, вычитая значение y0 из левой и правой частей, получим
y= x01x2+x02x1=k1 x1+k2 x2, где k1= x02; k2 =x01,
т.е. элемент умножения может быть приближенно представлен в виде сумматора и двух усилителей (линейных звеньев).
При использовании метода осреднения точность линеаризации оценивается величиной относительной погрешности (рис.2.3)
![]() ,
где ул
– уравнение линеаризованной характеристики.
Величина
должна быть
0,1
0,2.
,
где ул
– уравнение линеаризованной характеристики.
Величина
должна быть
0,1
0,2.
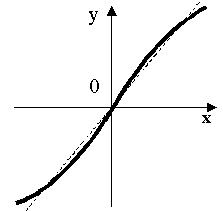
Рис.2.3. График относительной погрешности
Уравнения динамики сау
В общем виде линеаризованное дифференциальное уравнение одномерного элемента можно представить в виде (2.1):
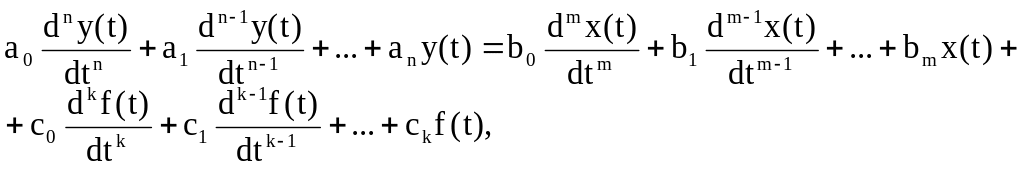
(2.1)
где y(t), x(t), f(t) – выходная, входная и возмущающая величины элемента или системы (в отклонения от состояния равновесия);ai, bi, ci - постоянные коэффициенты; n - порядок уравнения, при этом n m - условие физической реализуемости элемента.
Введем
оператор дифференцирования
![]() .
Тогда уравнение (2.1) может быть представлено
в операторном виде при нулевых начальных
условиях:
.
Тогда уравнение (2.1) может быть представлено
в операторном виде при нулевых начальных
условиях:
![]()
(2.2)
В выражении (2.2) полином, стоящий при выходном параметре Y, называется собственным оператором и обозначается D(p). Полиномы при воздействиях Х и F называются соответственно оператором управляющего воздействия и оператором возмущающего воздействия. Оператор управляющего воздействия обозначим K(p), а оператор возмущающего воздействия обозначим R(p). С учётом введенных обозначений уравнение (2.2) примет вид:
![]()
Если рассматривается только установившийся режим, то уравнение (2.2) примет вид:
Any=bmx + ckf. (2.3)
Таким образом, уравнение (2.2) описывает как динамику, так и статику работы САР, а уравнение (2.3) описывает только статику.
Следует отметить, что используемый выше оператор дифференцирования p имеет тесную связь с оператором интегрального преобразования Лапласа s, который является комплексной величиной. Как известно, для линейных дифференциальных уравнений с постоянными параметрами при нулевых начальных условиях и точностью до обозначения оператор p соответствует оператору s, т.е. p s.
Это обстоятельство позволяет использовать для решения уравнений типа (2.2), а также для моделирования САР интегральное преобразование Лапласа. Для перехода от реальных функций времени - оригиналов к их изображениям по Лапласу и обратно применяются прямое и обратное интегральные преобразования вида:
![]() ,
,
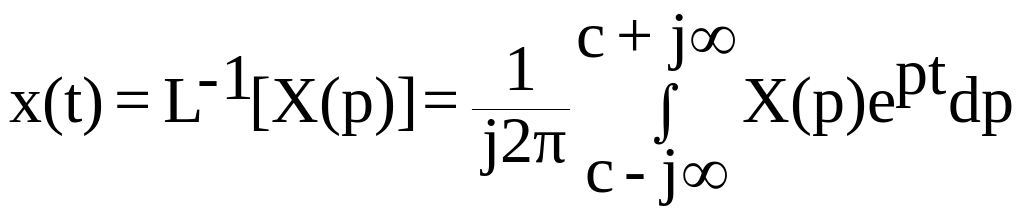 .
.
При этом x (t) называют оригиналом, а X(p) – изображением. Полагают, что функция x ( t ) обладает следующими свойствами:
- x ( t ) определена и кусочно - дифференцируема на всей положительной числовой полуоси (0-);
- x (t) = 0 при t < 0;
-существуют такие положительные числа M и С, при которых выполняется соотношение:
![]()
Для удобства и формализации решений уравнение (2.1) может быть представлено в одной из пяти стандартных форм:
в форме Коши;
в пространстве состояний;
в виде передаточных функций - W(p), Ф(p), Ф (p).
решение относительно регулируемой величины - y(t);
решение относительно ошибки - (t).
Форма Коши - матричная форма записи системы дифференциальных уравнений (ДУ), решенных исключительно относительно первой производной координат САУ.
Пространство состояний - матричная форма записи системы ДУ САУ, адаптированная для теории управления путем выделения из формы Коши алгебраических уравнений, связывающих внутренние координаты САУ с выходной(ыми). Применяется для описания САУ большого порядка, как правило, с несколькими входами / выходами и с перекрестными связями.
Под состоянием системы понимается минимально-необходимый набор переменных величин системы x1,x2,...,xn, способных однозначно и единственным образом определить положение системы в любой момент времени t. Совокупность переменных величин x1,x2,...,xn образует n-мерное пространство состояний Rn. Вектор с компонентами x1,x2,...,xn называется вектором состояния. Рассмотрим систему (рис.2.4) с m входами (u1,u2,...,um), r выходами (y1,y2,...,yr) и n переменными координатами (x1,x2,...,xn).

Рис. 2.4. Обобщенная структурная схема САУ
В общем случае обыкновенных линейных систем, описываемых системой дифференциальных уравнений в нормальной форме, рассматриваемая система может быть представлена следующей векторно-матричной формой
![]() ,
(2.4)
,
(2.4)
где X - вектор состояния системы, Y - вектор выходных управляемых величин, U - вектор входных воздействий (задающих и возмущающих); А, В, С, D - матрицы системы.
Уравнения (2.4) несут большой объем информации о динамических свойствах системы с m входами и r выходами при t0 t T. Первое уравнение из (2.4) определяет динамические характеристики системы и представляет собой компактную запись системы n линейных дифференциальных уравнений, разрешенных относительно производных первого порядка (нормальная форма Коши)
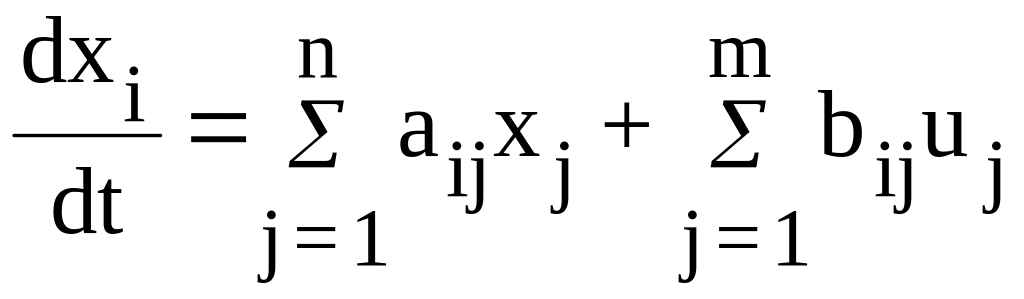 при
i=1,2, ... ,n, (2.5)
при
i=1,2, ... ,n, (2.5)
где aij и bij - постоянные коэффициенты.
Второе уравнение из (2.4) является уравнением выхода системы и представляет собой компактную запись системы r линейных алгебраических уравнений
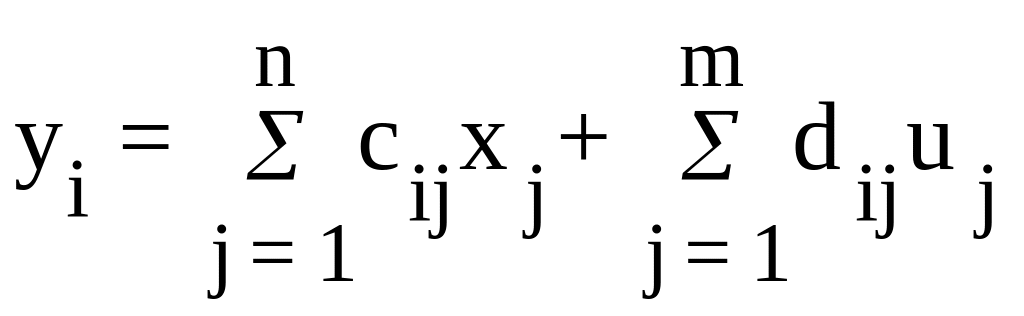 при
i=1,2, ... ,r, (2.6)
при
i=1,2, ... ,r, (2.6)
где cij и dij - постоянные коэффициенты.
В стандартной форме описания (2.4)
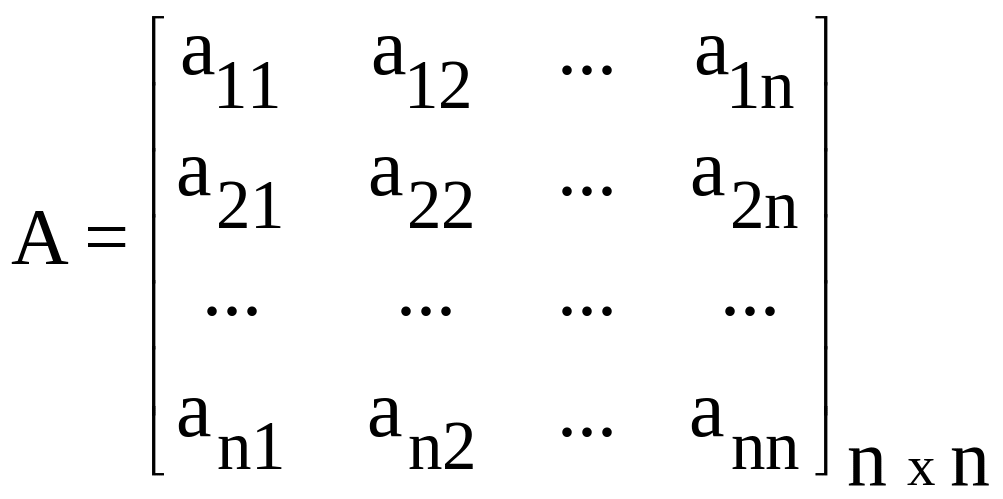 -
матрица системы;
-
матрица системы;
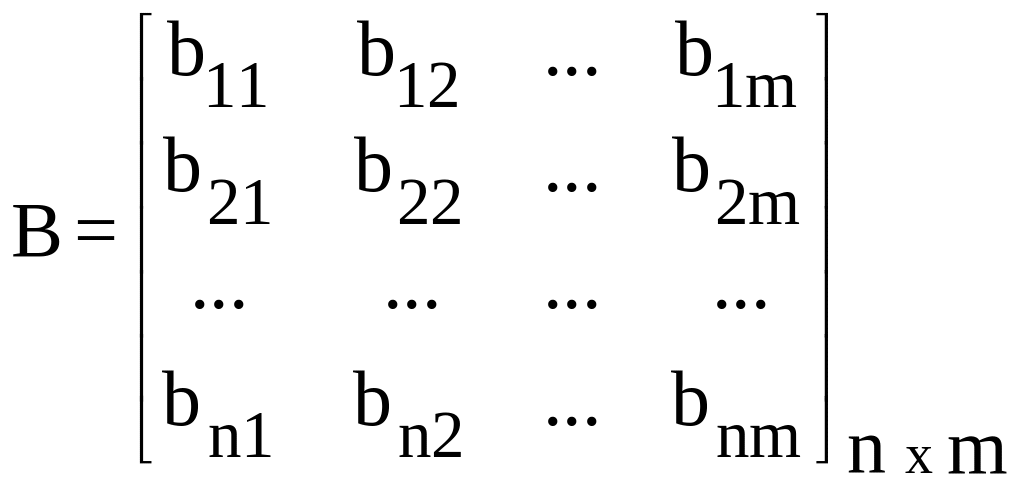 -
матрица управления;
-
матрица управления;
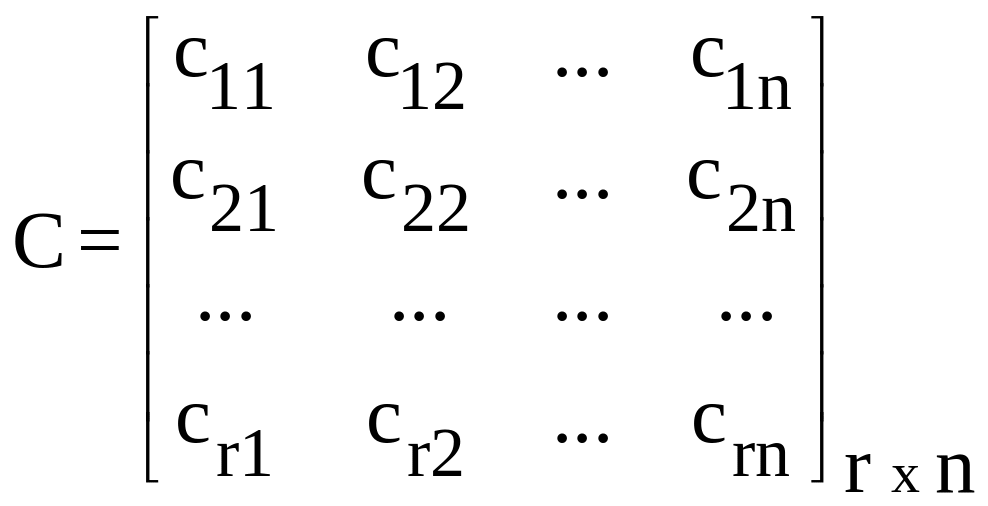 -
матрица наблюдения;
-
матрица наблюдения;
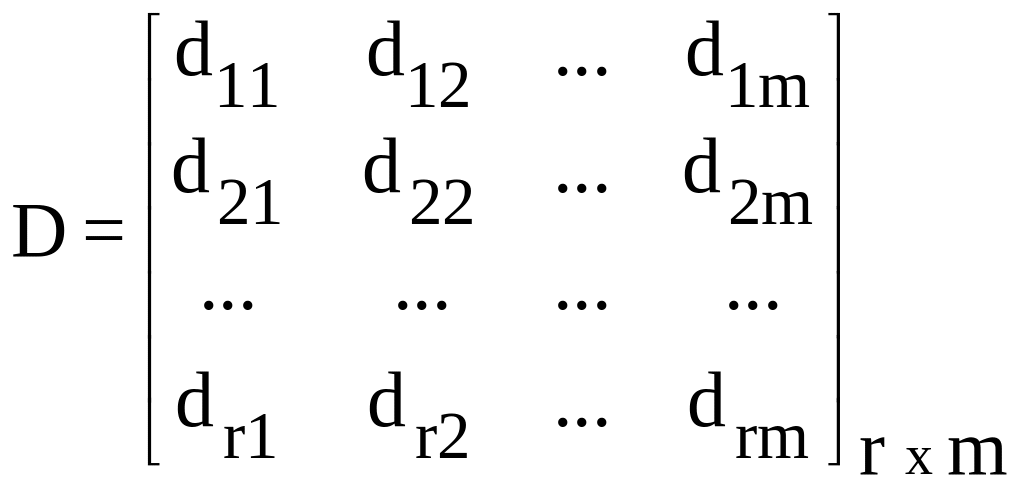 -
матрица связи.
-
матрица связи.
Матрица системы A, элементы которой определяются структурной схемой системы и значениями ее параметров, характеризует динамические свойства системы, ее свободное движение. Матрица управления B характеризует влияние внешних воздействий на переменные состояния системы, т.е. определяет чувствительность системы к внешним воздействиям (задающим и возмущающим). Матрица наблюдения C характеризует связь выходной величины системы с вектором состояния. Обычно не все составляющие вектора состояния являются наблюдаемыми сигналами, т.е. могут быть измерены с помощью каких-либо датчиков, в то время как выходной сигнал всегда наблюдаем. Матрица связи D устанавливает связь выходной величины системы с внешним воздействием. Таким образом, четверка матриц A, B, C, D полностью определяет систему управления.
П р и м е р. Написать уравнения состояния и построить электронную модель системы, имеющей матрицы состояния:
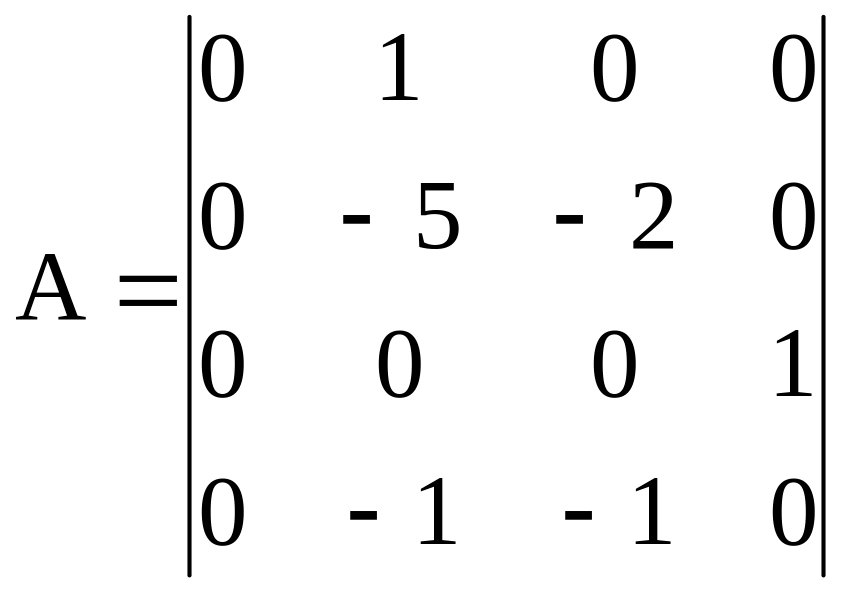 ;
;
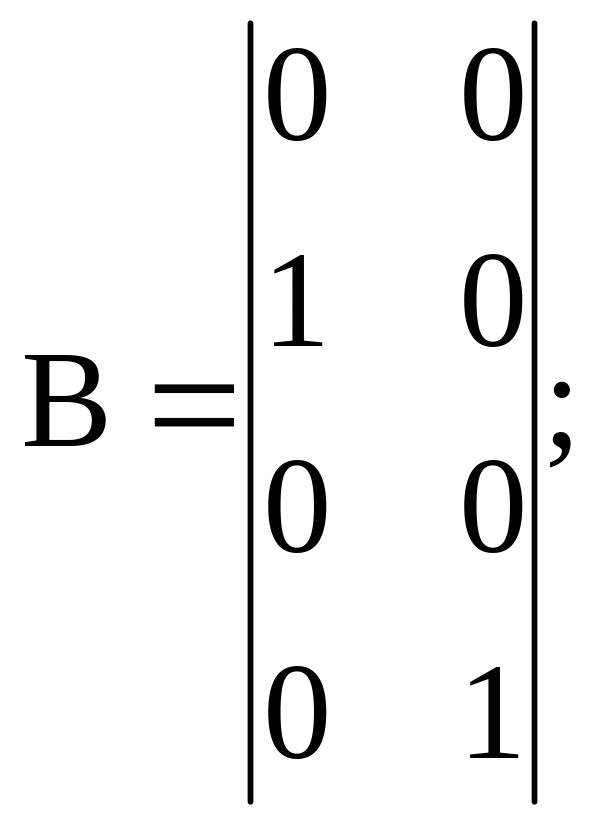 С=
С=![]() .
.
Р е ш е н и е. В соответствии с матрицами А, В и С уравнения состояния запишем в виде:
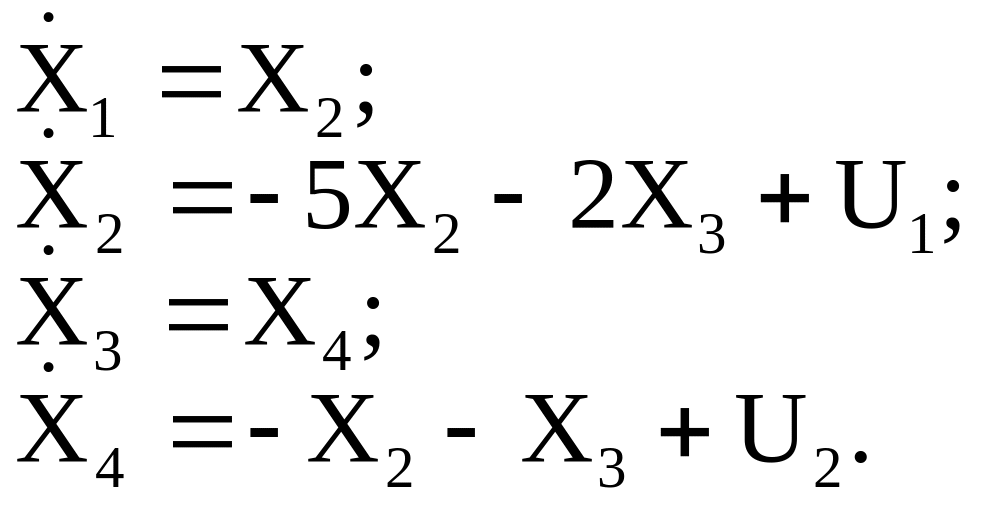
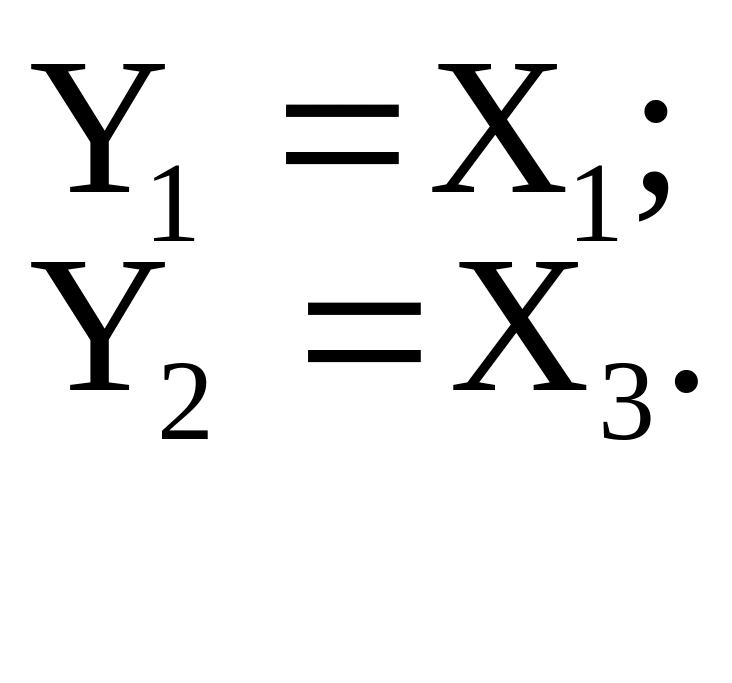
Тогда электронная модель с использованием идеальных интеграторов и усилителей будет иметь вид
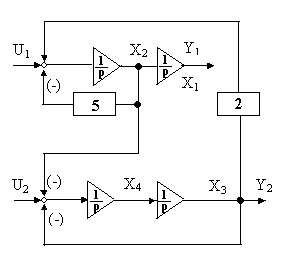
Матричные методы дают возможность обращаться с n уравнениями подобно тому, как это делается с одним уравнением. На рис.2.5 показана структурная схема системы управления, соответствующая стандартной форме описания систем в пространстве состояний; двойные линии на рисунке характеризуют векторные связи.
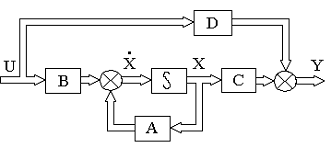
Рис. 2.5. Структурная схема системы в векторной форме:
- блок интеграторов; A,B,C,D - блоки матричных усилителей
Таким образом, уравнения переменных состояния представляют собой наиболее полное математическое описание динамики системы с несколькими входами и выходами и позволяют легко перейти к модели реальной системы и получить решение с применением вычислительной техники. Рассмотрим методику составления векторно-матричных дифференциальных уравнений для систем с одним входом и одним выходом:
![]() (2.7)
(2.7)
Выразим уравнение (2.7) относительно старшей степени р:
![]() (2.8)
(2.8)
Входной сигнал у (t) можно получить путем последовательного интегрирования старшей производной рn y(t). Для этого потребуется n последовательно включенных интеграторов, сигналы на входах которых представляют собой производные от рn y (t) до р y(t) (рис.2.6).
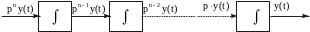
Рис. 2.6. Модель понижения порядка дифференциального уравнения
Согласно уравнению (2.8) очевидно, что старшая производная рn y(t) равна переменной bmf(t) минус сумма выходных сигналов интеграторов, умноженных на коэффициенты а1, а2 ... аn. Тогда получим структурную модель, представленную на рис. 2.7.
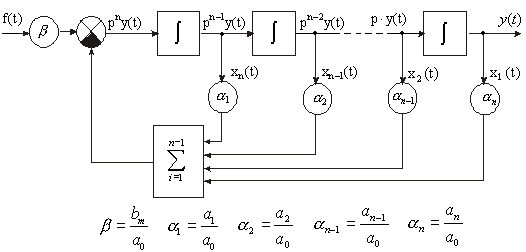
Рис.2.7. Модель САУ
Введем обозначения x1(t)=y(t), x2(t)=py(t)…xn(t)=pn-1y(t) и уравнение n-го порядка (2.7) запишем в виде системы n дифференциальных уравнений первого порядка:
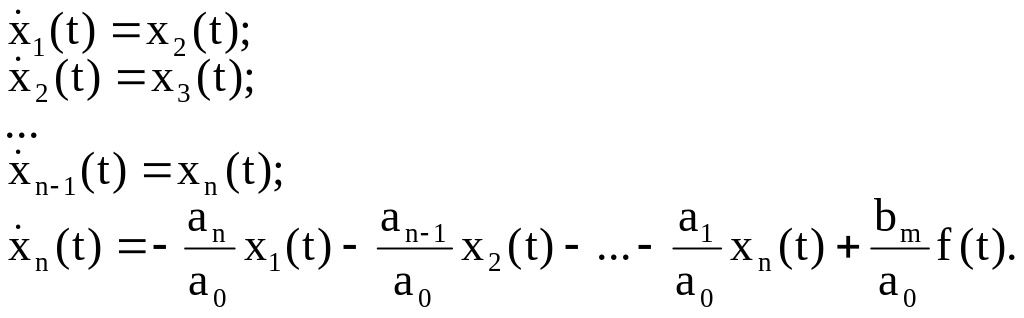
(2.9)
Система уравнений (2.9) является одной из форм представления динамических процессов структурной модели, изображенной на рис. 2.7.
В матричной форме система уравнений (2.9) имеет вид:
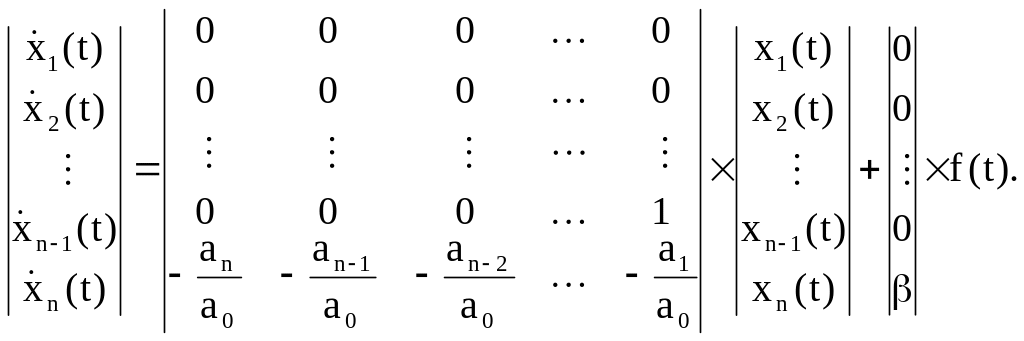
В сокращенном виде матричная форма записывается следующим образом:
![]() x’(t)=Ax(t)+B(t),
x’(t)=Ax(t)+B(t),
где
![]() n-мерный
вектор состояния; A
– квадратная матрица размером n
n;
B -
n-мерный
вектор состояния; A
– квадратная матрица размером n
n;
B -
![]() - вектор-столбец управления.
- вектор-столбец управления.
Ввиду того, что имеется множество эквивалентных (с точки зрения входо-выходных соотношений) способов представления уравнений состояния системы, можно выбрать из них "наилучшие" - наиболее удобные для использования в рассматриваемой задаче. Такие формы записи уравнений называются каноническими. Поскольку может быть много различных приложений, известно и много канонических форм [25]. Наиболее распространенные из них: блочно-диагональная вещественная форма Жордана; управляемая форма Луенбергера (матрица Фробениуса). На рис.2.7 приведен пример представления системы матрицей Фробениуса, когда характеристическое уравнение располагается в последней строке.
Структурная математическая модель динамических процессов САУ обладает рядом преимуществ перед аналитическими описаниями или передаточными функциями. Во-первых, структурная модель дает ясное и наглядное представление понятию "состояние систем", как совокупность сигналов на выходах интеграторов. Во-вторых, однозначно представляется структура взаимодействий между переменными в виде системы с обратными связями, которые и определяют протекание динамических процессов. Одновременно структурные модели оказывают помощь при моделировании САУ на аналоговых или цифровых вычислительных машинах.
П р и м е р. Начертить блок-схему и написать уравнения состояния системы, описываемой дифференциальным уравнением
![]() ,
,
где g – входная величина; y – выходная величина.
Р
е ш е н и е. Разрешим уравнение относительно
старшей производной
![]() и составим блок- схему ее получения
рис.2.8.
и составим блок- схему ее получения
рис.2.8.
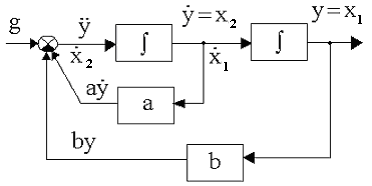
Рис.2.8. Блок-схема системы
В соответствии с выбранными переменными состояния на рис.2.8 запишем уравнения в нормальной форме
![]()
Или в матричной форме
![]()
где
![]()
![]()
![]()
![]()
