Свойства неопределенного интеграла:
1.
.
2.
–
постоянный множитель можно выносить
за знак интеграла.
3.
–
интеграл от суммы функций равен сумме
интегралов от этих функций.
Практика нахождения интегралов, как правило, заключается в таком преобразовании подынтегральной функции, которое позволяет привести данный интеграл к табличному. Рассмотрим приемы преобразования подынтегральных функций на конкретных примерах.
Задача
12.
Найти
интеграл
.
Решение. Преобразуем подынтегральную функцию, а затем применяем свойства неопределенного интеграла и табличные интегралы
и
.
Получаем
=
=
=
=
=
=
=
.
Задача 13.
Найти интеграл
.
Решение.
Чтобы привести данный интеграл к
табличному
,
положим
,
тогда
.
Произведем замену в подынтегральном
выражении
=
=
.
Задача 14.
Найти интеграл
.
Решение.
Чтобы привести данный интеграл к
табличному, положим
.
Тогда
или
.
Отсюда
.
Выполнив замену в подынтегральном
выражении, получаем
=
=
=
=
=
=
=
.
Задача №15.
Найти интеграл
.
Решение.
Чтобы привести данный интеграл к
табличному, положим
.
Тогда
или
.
Выполнив некоторые преобразования
подынтегрального выражения, произведем
замену переменной:
=
=
=
.
Задача
16.
Найти
интеграл
.
Решение.
Чтобы привести данный интеграл к
табличному
,
положим
,
тогда
или
.
Заметив, что числитель подынтегрального
выражения отличается от дифференциала
переменной t
лишь на постоянный множитель,
произведем замену
=
=
=
=
.
Задача
17. Найти
интеграл
.
Решение.
Для нахождения данного интеграла
применим формулу интегрирования по
частям:
.
Положим
,
.
Тогда
,
.
Отсюда
.
В
интеграле применим
подстановку
,
откуда
,
или
.
Следовательно,
=
=
=
.
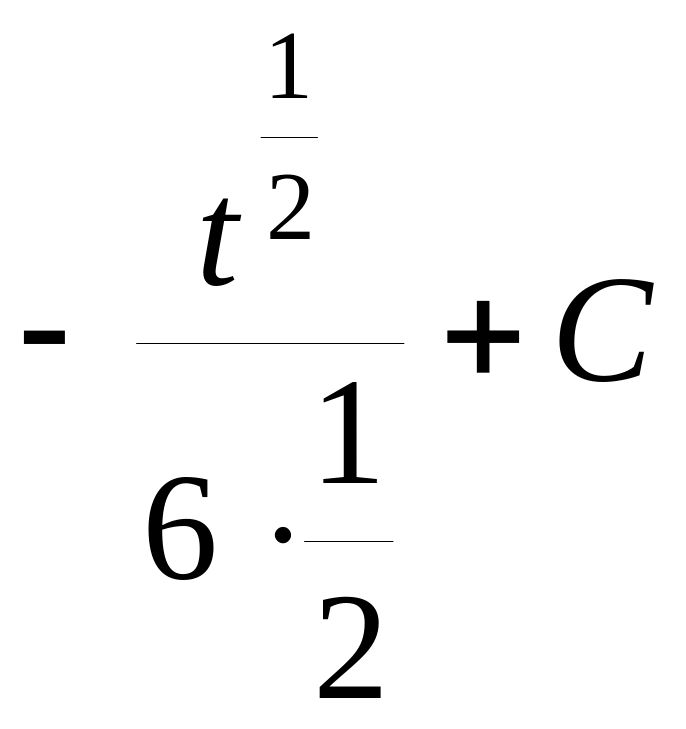Окончательно
имеем:
.
Задача
18.
Найти
интеграл
.
Решение.
Для нахождения данного интеграла также
используем формулу интегрирования по
частям. Положим u=x2
и
dv=sinxdx.
Тогда
du=2xdx
и
.
Отсюда
= -x2cosx
+
= -x2cosx
+
.
Для
нахождения
опять
воспользуемся методом интегрирования
по частям, положив u=x,
а dv=cosx
dx.
Тогда du=dx
и v=sinx.
Окончательно
получим
=
Вопросы для самопроверки
1. Какая функция называется первообразной для данной функции?
2. Дайте определение неопределенного интеграла от данной функции.
3. Сформулируйте основные свойства неопределенного интеграла.
4. В чем сущность интегрирования методом замены переменной?
5. Выведите формулу интегрирования по частям.
Тема 6. Определенный интеграл и его приложения
Литература: 1. Шипачев В.С. Высшая математика. М. Высшая школа. 2008. Гл. 8.
2. Красс М.С. Математика для экономических специальностей. М. Дело. 2002. Гл. 7.
Методические указания
Под определенным
интегралом
от данной непрерывной функции
на данном отрезке [a;
b]
понимается соответствующее приращение
ее первообразной, то есть
.
Числа а
и b
называются соответственно верхним и
нижним пределом интегрирования. Обычно
разность
обозначают как
,
в силу чего формулу определенного
интеграла обычно записывают так
,
причем следует помнить, что сначала подставляется верхний предел интегрирования, а затем нижний.
Определенный интеграл имеет также геометрический смысл, заключающийся в том, что он равен площади криволинейной трапеции, то есть такой трапеции, одна из непараллельных сторон которой представляет собой график функции на интервале [a; b].
Вычисление определенных интегралов также представляет собой приведение с помощью различных приемов данного интеграла к табличному
Задача 19. Вычислить определенный интеграл
.
Решение.
Данный интеграл приводится к табличному
с помощью подстановки t
= lnx.
Отсюда
.
Определим пределы интегрирования новой
переменной. При х
= 1, t
= ln1
= 0, при х
= е, t
= lne
= 1. Произведем замену переменной и
используем формулу Ньютона–Лейбница.
=
=
= arcsin1
– arcsin0
=
.
Задача 20. Найти площадь фигуры, ограниченной линиями:
y
= x2,
,
y
= 0, x
= 2 (x
> 0).
Решение. Данную фигуру можно разбить на две криволинейные трапеции, площади которых соответственно равны: S1 и S2. (Рис. 4).
Тогда S = S1 + S2. Найдем абсциссу точки А –точки пересечения двух линий.
у
2,0
1,5
1,0
0,5 у = 1/х
0 0,5 1,0 1,5 2,0 2,5 х
Рис. 4
Найдем пределы интегрирования, решив систему уравнений
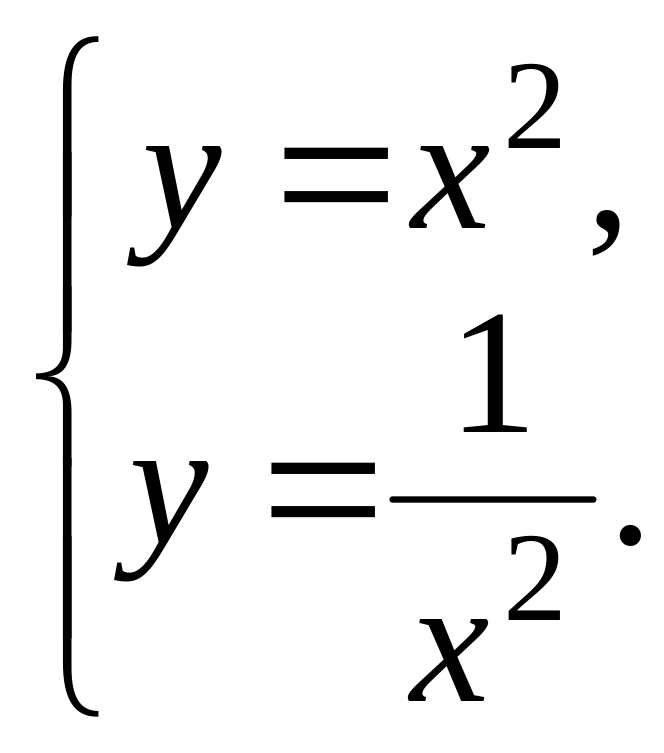
Отсюда
,
или х4
= 1, то есть х1
= –1 и х2
= 1.
Так как по условию x > 0, то абсцисса точки А равна 1. Следовательно,
=
,
и тогда
( кв.ед.).
Задача 21. Найти площадь фигуры, ограниченной параболой
и прямой y
= x
+ 2.
Решение. 1. Изобразим данные линии на чертеже и заштрихуем фигуру, площадь которой нужно найти. Графиком функции является парабола.
Найдем производную данной функции и, приравняв ее к нулю, определим критическую точку.
.
Пусть y′
= 2 – х
= 0. Отсюда х
= 2. Это –
абсцисса вершины параболы. Ордината
вершины
.
Ветви параболы направлены вниз. Найдем
точки пересечения параболы с осью Ох,
положив у
= 0. Тогда
или
.
Решив данное квадратное уравнение,
получим его
корни: х1
= -2 и х2
= 6. Строим параболу (рис. 5).
2. Графиком функции у = х + 2 является прямая, для ее построения достаточно двух точек. При х = 0, у = 2, при х = 2, у = 4. Строим прямую.
3. Площадь фигуры,
ограниченной сверху непрерывной кривой
,
снизу –
непрерывной кривой
находится по формуле:
,
где a и b – абсциссы точек пересечения кривых.
у
8
у = х + 2
6
4
2
–2 0 2 4 6 х
Рис. 5
Для нахождения точек пересечения данных линий, решим систему уравнений
,
или
.
Решая полученное квадратное уравнение, получим х1 = –2 и х2 = 4, следовательно, а = –2; b = 4. Применяя формулу площади, составим интеграл
,
т. е., искомая площадь S = 18 (кв. ед.).
Вопросы для самопроверки
1. Дайте определение определенного интеграла от данной функции на заданном отрезке?
2. Каков геометрический смысл определенного интеграла?
3. Напишите формулу Ньютона-Лейбница.
4. Сформулируйте свойства определенного интеграла.
5. Как используется способ подстановки для вычисления определенного интеграла?
6. Напишите формулу интегрирования по частям для вычисления определенного интеграла.
7. Как вычисляется площадь плоской фигуры в прямоугольной системе координат с помощью определенного интеграла?