Тема 3. Исследование функции с помощью производной
Литература: 1. Шипачев В.С. Высшая математика. М. Высшая школа. 2008. Гл. 6.
2. Красс М.С. Математика для экономических специальностей. М. Дело. 2002. Гл. 5.
Методические указания
Исследование функции предусматривает нахождение области ее определения, точек экстремума и интервалов возрастания и убывания, а также точек перегиба и интервалов выпуклости и вогнутости графиков функции.
Областью
определения функции
называется совокупность значений ее
аргумента, для которых функция имеет
смысл или, как говорят, функция определена.
Например, областью определения функции
является интервал
,
так как при отрицательных значениях х
она не
определена, а функции
–
интервал
,
так как знаменатель дроби не может быть
равным нулю.
Экстремумом
функции
называется собирательное значение
максимума
или минимума
этой функции в какой-либо точке. Согласно
теореме Ферма, если функция
в точке экстремума
имеет производную, то эта производная
равна нулю.
.
Интервал значений аргумента, при котором с увеличением аргумента функция также увеличивается, называется интервалом возрастания функции. И наоборот, интервал, при котором с уменьшением аргумента функция уменьшается – интервалом убывания. На интервале возрастания первая производная функции положительна, соответственно, на интервале убывания – отрицательна.
Точками перегиба
функции
называются такие значения ее аргумента,
при которых рост возрастающей функции
останавливается, но затем, по мере
дальнейшего увеличения аргумента,
возобновляется. Тоже самое относится
и к убывающей функции. В точках перегиба
функции, и ее первая, и вторая производные
равны нулю.
.
Интервалом вогнутости функции называется совокупность значений аргумента, при которых возрастает ее первая производная, то есть вторая производная функции положительна. Аналогично, интервал выпуклости функции, это совокупность значений аргумента при которых убывает первая производная, и, соответственно, вторая производная отрицательна.
Рассмотрим исследование функции на конкретном примере.
Задача
9. Исследовать
функцию
с помощью производной и построить ее
график.
Решение. 1. Находим область определения функции.
Выражение
имеет смысл при любом действительном
значении аргумента х,
следовательно, областью определения
функции является множество действительных
чисел
.
2. Находим первую производную заданной функции
или
.
3. Критическими
точками функции
называются точки, в которых производная
равна нулю или не существует. Найдем
их:
,
т. е.
или
.
Согласно решению
квадратного уравнения
,
и
.
Других критических точек нет.
4. Обращение производной функции в нуль или ее отсутствие в точках, где функция определена, есть лишь необходимое условие существования экстремума функции в этих точках.
Достаточным условием существования экстремума функции в критической точке, входящей в область определения функции, является изменение знака производной первого порядка при переходе через эту точку. В частности, если производная меняет знак с плюса на минус, то в критической точке функция имеет максимум. Если же при переходе через критическую точку производная меняет знак с минуса на плюс, то в этой точке функция имеет минимум.
Определим, являются ли точки и точками экстремума. Они разбивают всю числовую ось на три промежутка, (рис. 1), знак производной в которых определим с помощью «пробной» точки.
●
●
1 5 х
Рис. 1
В интервале (–∞; 1) возьмем, например, точку х = 0. Тогда
.
В интервале (1; 5) возьмем точку х = 2. Очевидно
.
Наконец, в интервале (5; ∞) возьмем точку х = 6. Тогда
.
Следовательно, точка х = 1 есть точка максимума данной функции, а точка х = 5 – точка минимума. Найдем значение функции в точках экстремума:
уmax
= y(1)
=
(13
– 9∙12
+ 15∙1 – 3 ) = 1.
уmin = у(5) = (53 – 9∙52 + 15∙5 – 3) = – 7.
5. Если производная функции положительна внутри некоторого промежутка, то функция возрастает на этом промежутке. Если же производная отрицательна внутри некоторого промежутка, то функция убывает на этом промежутке.
Очевидно, данная функция возрастает на промежутках (–∞; 1) и (5; ∞), а убывает на промежутке (1; 5).Результат исследований п. 4 и п. 5 удобно представить в виде схемы.
6. Найдем вторую производную у″(х) данной функции
у″(х) = (3х2 – 18х + 15)′ = (6х – 18).
Найдем точки, в которых вторая производная функции равна нулю
(6х - 18) = 0, откуда х = 3.
+
–
+
•
•
1
5 х
max min
Рис. 2
Точка х = 3 разбивает всю числовую ось на два интервала (–∞; 3) и (3; ∞). В интервале (–∞; 3) возьмем, например, точку х = 0 и определим в ней знак второй производной
у″(0)
=
(6∙0 – 18) =
< 0.
В интервале (3; ∞) возьмем, например, точку х = 4, тогда
у″(4)
=
(6∙4 – 18) =
> 0.
Если вторая производная f″(х) положительна внутри некоторого промежутка, то график этой функции на этом промежутке вогнутый вверх (или выпуклый вниз). Если же вторая производная f″(х) внутри некоторого промежутка отрицательна, то график функции на этом промежутке выпуклый вверх (или вогнутый вниз).
Очевидно, на интервале (–∞; 3) график данной функции выпуклый вверх, а на промежутке (3; ∞) – вогнутый вверх.
7. Если вторая
производная f″(х)
в некоторой точке х0,
принадлежащей области определения
функции, обращается в нуль и при переходе
через эту точку меняет знак, то точка
является точкой перегиба графика
функции
.
Итак, х
= 3 – абсцисса точки перегиба. Найдем ее
ординату
у(3) = (33 – 9∙32 + 15∙3 – 3) = (–12) = –3.
Таким образом, точка (3; -3) - точка перегиба графика функции.
8. Строим график функции у = (х3 – 9х2 + 15х – 3) (рис. 3).
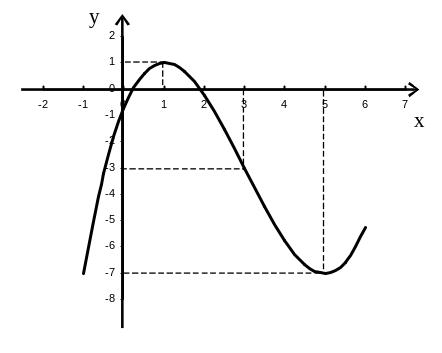
Рис. 3
Вопросы для самопроверки
1. Сформулируйте признаки возрастания (убывания) функции в данном промежутке.
2. Какие точки называются критическими? Как найти эти точки?
3. Сформулируйте необходимые условия существования экстремума функции.
4. Сформулируйте достаточные признаки существования экстремума функции.
5. Дайте определение выпуклости, вогнутости кривой.
6. Что называется точкой перегиба графика функции?
7. Какова схема исследования функции на экстремум с помощью производной?