Тема 2. Производная и дифференциал функции
Литература: 1. Шипачев В.С. Высшая математика. М. Высшая школа. 2008. Гл. 5.
2. Красс М.С. Математика для экономических специальностей. М. Дело. 2002. Гл. 4.
Методические указания
Производной
функции
называется выражение, характеризующее
быстроту изменения функции при изменении
ее аргумента. Например, если мы имеем
функцию
,
то, очевидно, быстрота ее изменения
равна 5, то есть изменение аргумента на
единицу приводит к изменению значения
функции на 5 единиц. (
,
а
).
В общем случае
производная
функции
определяется
как предел отношения приращения функции
к приращению
ее аргумента
.
Очевидно,
что если
,
то
,
и
.
Производная функции
обозначается штрихом около символа
функции
.
Таким образом, согласно определению
.
Рассмотрим несколько примеров нахождения производных некоторых функций.
1. Степенная функция.
Пусть
.
Тогда, согласно определению,
.
Для устранения неопределенности раскроем скобки в числителе
Теперь
возьмем
.
Тогда
.
Также раскрываем скобки в числителе и
получаем
.
Производные функций с показателями степени, превышающие третью можно получить с помощью бинома Ньютона
,
где
- число сочетаний из n
по k.
В развернутом виде формула бинома
Ньютона имеет вид
,
где,
в нашем случае,
,
Легко проверить,
что если
,
то
.
Отсюда следует общая формула производной
степенной функции
.
Нахождение производной функции называется
дифференцированием.
Основные формулы дифференцирования
1.
.
11.
.
2.
.
12.
.
3.
.
13.
.
4.
.
14.
.
5.
.
15.
.
6.
.
16.
.
7.
.
17.
.
8.
.
18.
.
9.
.
19.
.
10.
20.
Рассмотрим примеры нахождения производных различных функций на конкретных примерах.
Задача 6. Найти производную функции
.
Решение. Применяем формулу (5) дифференцирования произведения
.
Далее используем формулу (2) и формулу (3) дифференцирования алгебраической суммы
.
При дифференцировании алгебраической суммы к первому слагаемому применим формулу (7), ко второму (4), к третьему (1), получим
.
Затем используем формулу (11)
=
.
Задача 7. Найти производную функции
.
Решение. Используем формулу (3) дифференцирования алгебраической суммы
.
К первому слагаемому применяем формулу (6) дифференцирования частного, а ко второму формулу (11)
.
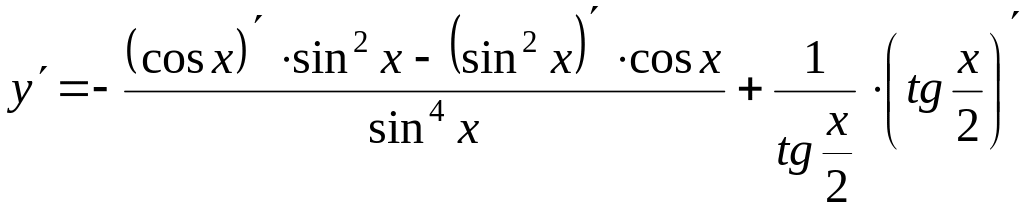Далее используем формулы (13), (7) и (14)
.
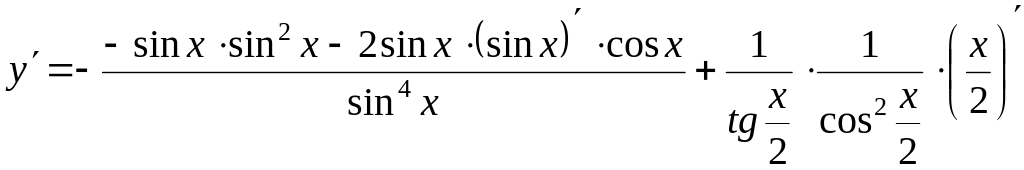Для получения окончательного ответа осталось использовать формулы (12), (4) и (2), а также выполнить преобразования
=
=
=
.
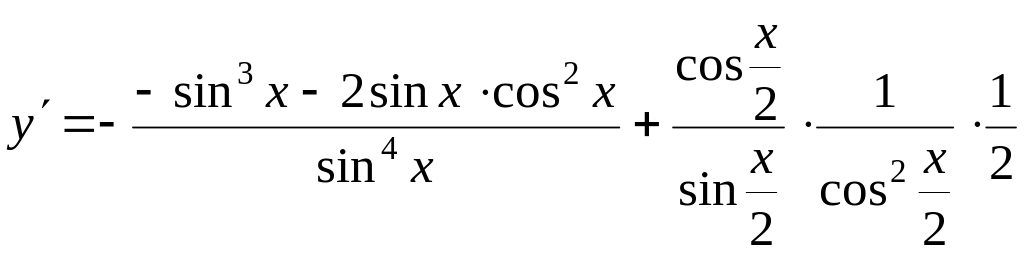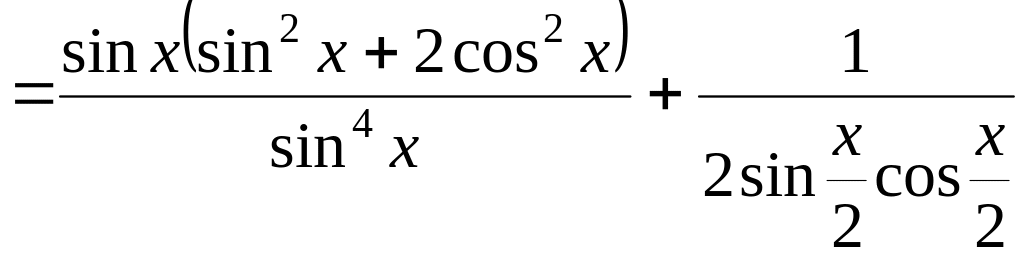Задача 8. Найти производную функции
.
Решение. В данном случае удобнее вначале упростить данную формулу, используя свойства логарифмов
=
=
.
Далее, пользуясь правилами дифференцирования и таблицей производных, получаем
=
=
=
.
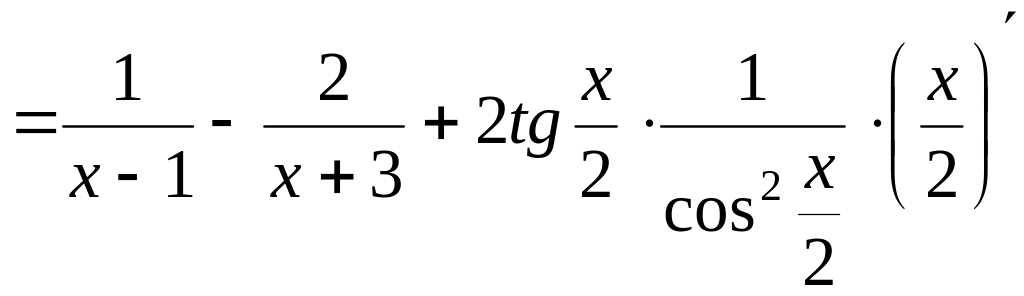
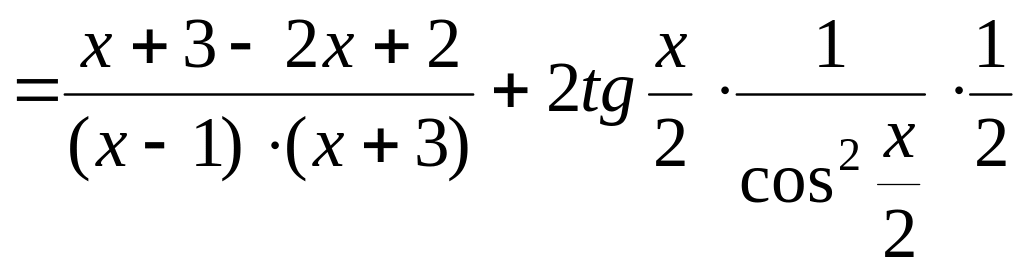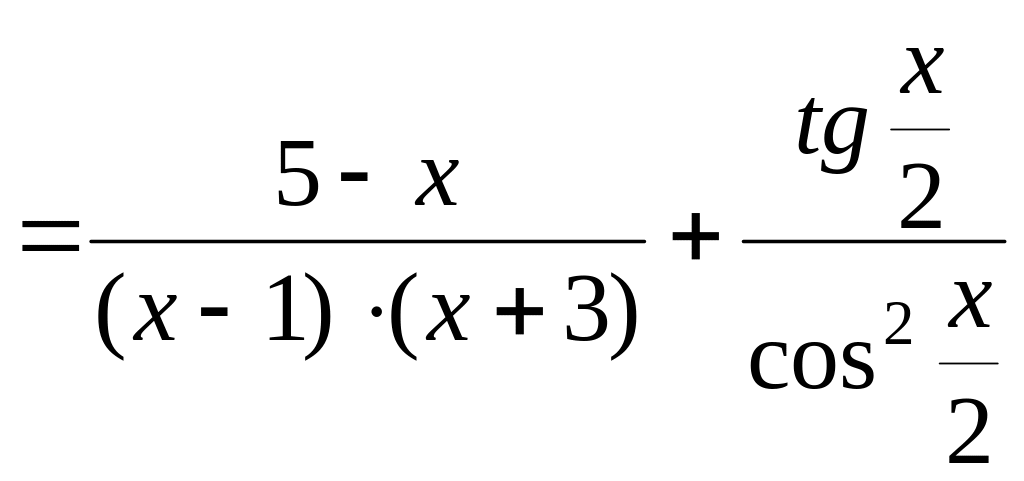Вопросы для самопроверки
1. Дайте определение производной функции.
2. Каков геометрический смысл производной?
3. В чем заключается физический смысл производной?
4. Сформулируйте правила дифференцирования суммы, произведения, частного.
5. Приведите формулы дифференцирования основных элементарных функций.
6. Сформулируйте правило дифференцирования сложной функции.
7. Что называется дифференциалом функции? Каков его геометрический смысл?
8. Что называется производной второго порядка? Каков физический смысл производной второго порядка?