9.Нахождение наибольшего и наименьшего значения непрерывной функции на отрезке.

Определение 9.1

Пусть функция y=f( x ), определена и непрерывна на промежутке [a,b], достигает на нем своего наибольшего (наименьшего) значения, если существует точка c, принадлежащая этому промежутку, такая, что для всех х из [a,b] выполняется неравенство

.

Функция, непрерывная на отрезке, достигает на нем своего наибольшего и наименьшего значений.

Наибольшее значение М и наименьшее значение m непрерывной функции могут достигаться как внутри отрезка, так и на его концах. Если наибольшего (наименьшего) значения функция достигает во внутренней точке отрезка, то эта точка является точкой экстремума.

Алгоритм отыскания наибольшего и наименьшего значений непрерывной функции y = f( x ) на отрезке [a,b]:

1. Найти ;

2. Найти точки, в которых или не существует, и отобрать из них те, что лежат внутри отрезка [a,b];

3. Вычислить значения функции y=f( x ) в точках, полученных в п.2, и на концах отрезка и выбрать из них наибольшее и наименьшее; они и будут соответственно наибольшим и наименьшим значениями функции y=f( x ) на отрезке [a,b], которые можно обозначить так: .

Если поставлена задача найти для непрерывной на ( a,b ) функции y=f( x ), то она решается по тому же правилу, что соответствующая задача для отрезка [a,b].

Замечание: на третьем этапе вместо вычисления значений функции на концах отрезка находят пределы функции при приближении к концам интервала.

Иногда для отыскания наибольшего или наименьшего значения непрерывной функции y=f( x ) на промежутке (a,b)полезны два утверждения:

1. Если функция y=f( x ) имеет в промежутке Х только одну точку экстремума x=c , причем это точка максимума, то f(c)- наибольшее значение функции на промежутке Х;

2. Если функция y=f( x ) имеет в промежутке Х только одну точку экстремума x=c, причем это точка минимума, то f(c)- наименьшее значение функции на промежутке Х.

III.Применение производной

Применение физического смысла производной при решении физических задач

Применение производной в физике очень обширно. Рассмотрим несколько примеров применения производной в физических задачах.

Механическое движение - это изменение положения тела в пространстве относительно других тел с течением времени.

Основной характеристикой механического движения служит скорость:

Алгоритм нахождения скорости тела с помощью производной.

Если закон движения тела задан уравнением:

s = s ( t ),

то для нахождения мгновенной скорости тела в какой-нибудь определенный момент времени надо:

1.Найти производную s' (t )

2. Подставить в полученную формулу заданное значение времени.

Пример:

Автомобиль приближается к мосту со скоростью 72 км/ч. У моста висит дорожный знак "36км/ч". За 7 сек до въезда на мост, водитель нажал на тормозную педаль. С разрешаемой ли скоростью автомобиль въехал на мост, если тормозной путь определяется формулой :

s=20t - t²

тогда действуя по алгоритму, написанному выше, запишем решение:

S'(t)= (20t- t²)'=20-2t

V=s'(t)=20-2 7=6 м/c.

Да, т.к. скорость через 7 сек. будет равна 6м/с (21,6 км/ч).

Производная в электротехнике

В наших домах, на транспорте, на заводах: всюду используется электрический ток.

Под электрическим током понимают направленное движение свободных электрически заряженных частиц.

Количественной характеристикой электрического тока является сила тока.

В цепи электрического тока электрический заряд меняется с течением времени по закону q=q (t). Сила тока I есть производная заряда q по времени.

В электротехнике в основном используется работа переменного тока.

Электрический ток, изменяющийся со временем, называют переменным. Цепь переменного тока может содержать различные элементы: нагревательные приборы, катушки, конденсаторы.

П олучение переменного электрического тока основано на законе электромагнитной индукции, формулировка которого содержит производную магнитного потока.

Пример:

Заряд, протекающий через проводник, меняется по закону

Найти силу тока в момент времени t = 5 секунд

Решение:

q'=2 cos(10-2t)

I=2 = 2

Ответ: Сила тока равна 2 А.

А также :

Сила есть производная работы по перемещению,

т.е. F=A ^'(x)

Теплоемкость – есть производная теплоты по температуре, т.е.

C(t) = Q (t)

Пример

Пусть Q ( t )-количество теплоты, которое необходимо для нагревания тела массой 1 кг, от 0⁰С до температуры t⁰ (по Цельсию).

Известно, что в диапазоне 0⁰ до 95⁰, формула

Q ( t ) = 0,396t + 2,08110^-3t² - 5,02410^-7t ³

дает хорошее приближение к истинному значению. Найдите, как зависит теплоёмкость воды от t.

Решение. C ( t ) = Q ( t ) = 0,396 + 4,162*10 ^-3 t – 15,072*10 ^-7 t²

Производная в химии

И в химии нашло широкое применение дифференциальное исчисление для построения математических моделей химических реакций и последующего описания их свойств.

Химия – это наука о веществах, о химических превращениях веществ.

Химия изучает закономерности протекания различных реакций.

Скоростью химической реакции называется изменение концентрации реагирующих веществ в единицу времени.

Так как скорость реакции v непрерывно изменяется в ходе процесса, ее обычно выражают производной концентрации реагирующих веществ по времени.

Если C(t) – закон изменения количества вещества, вступившего в химическую реакцию, то скорость v(t) химической реакции в момент времени t равна производной:

Сопоставим понятия:

Понятие на языке химии	Обозначение	Понятие на языке математики
Количество вещества в момент t0	c = c(t)	функция
Интервал времени	∆t = t2 – t1	приращение аргумента
Изменение количества вещества	∆c = c(t+ t ) – c(t)	Приращение функции
Средняя скорость химической реакции		Отношение приращения функции к приращению аргумента

Скорость химической реакции в данный момент времени, определяется по формуле:

V (t) = c (t) , (где с-конценрация).

Найти скорость реакции в момент времени t = 10сек, если концентрация исходного продукта меняется по закону:

v( t )= 10

Подставим значение времени в полученное выражение:

Скорость реакции в данный момент времени приблизительно будет равна 1.37.

Производная в биологии.

Сопоставим понятия на языке биологии и математики и заметим, что и в этой сфере также широко применяется производная.

Понятие на языке биологии	Обозначение	Понятие на языке математики
Численность в момент времени t1	x = x( t )	Функция
Интервал времени	∆t = t2 – t1	Приращение аргумента
Изменение численности популяции	∆x = x(t2) – x(t1)	Приращение функции
Скорость изменения численности популяции		Отношение приращения функции к приращению аргумента
Относительный прирост в данный момент		Производная

Производная в демографии.

Идея социологической модели Томаса Мальтуса состоит в том, что прирост населения пропорционально числу населения в данный момент времени t через N(t), . Модель Мальтуса неплохо действовала для описания численности населения США с 1790 по 1860 годы. Ныне эта модель в большинстве стран не действует.

Выполним ряд простейший преобразований и выведем формулу для вычисления численности населения на ограниченной территории в момент времени t.

Опираясь на данную модель знаменитого демографа, попробуем выяснить возможность применения производной в этой сфере.

Пусть у = у(t)- численность населения.

Рассмотрим прирост населения за t = t-t₀

y = k y t, где k = k_р – k_с –коэффициент прироста (k_р – коэффициент рождаемости,

k_с – коэффициент смертности)

=k y

При t 0 получим = y

у = к у

Вследствие, проведенных нами преобразований можно сделать вывод, что и здесь производная широко применима и дает устойчивую систему решений определенных вопросов в этой сфере.

Производная в экономике.

В особенности применение производной востребовано в экономике.

Давайте рассмотрим применение производной к решению следующей экономической задачи:

Р - ежегодное потребление продукта на душу занятых в производстве;

x- число занятых в производстве рабочих.

Величины Р и x связаны следующей функциональной зависимостью

, M ,b- постоянные, характеризующие производственные возможности хозяйства.

При M=250,b=8464 определить число рабочих, соответствующее наибольшему значению Р в хозяйствах с 80,90,120 и 150 рабочими местами.

Решение

(раскроем скобки и представим дробь в виде разности трёх переменных).

Исследуем функцию на наибольшее значение при х >0. Для этого найдём производную и прировняем её к нулю:

Так как х >0, то .

Исследуя знак производной, легко убедиться в том, что функция монотонно возрастает, а при х >92- монотонно убывает .

Следовательно, на отрезке от 1 до 80 функция возрастает, и её наибольшее значение достигается на правом конце х=80.

А на отрезках от 1 до 120 и от 1до 150 функция меняет характер монотонности, отсюда следует, что наибольшее значение достигает в точке

х = 92.

Производная помогла определить, что хозяйству нет смысла набирать 120 и 150 человек для достижения наибольшей прибыли.

2.П (t) = υ (t) - производительность труда,

где υ (t) - объем продукции

J(x) = y (x) - предельные издержки производства,

где y– издержки производства в зависимости от объема выпускаемой продукции x.

2.Оборот производительности труда за истекший год описывается через функцию  U(t)=0,15t³ – 2t² + 200, где t – месяцы,U -денежные единицы

Исследуйте оборот предприятия за 9 и 10 месяцы.

Решение. Исследуем оборот предприятия с помощью производной: U'(t)=0,45t² - 4t 

V(t)=U (t)

Подставим t:

V( )=0.45

V( )=0.45

V( )<v( )

Сравнивая показатели, обнаружим что оборот производительности труда предприятия на 9 месяце был значительно меньше, чем на 10.

3.Функция спроса имеет вид Q_D=100 – 20p, постоянные издержки TFC (total fixed costs) составляют 50 денежных единиц, а переменные издержки TVC (total variable costs) на производство единицы продукции – 2 денежные единицы. Найти объём выпуска, максимизирующий прибыль монополиста.

Решение: Прибыль есть выручка(TR) минус издержки (TC):

П=TR – TC,

где TR= p*Q (p-цена товара,Q-количество товара);

TC=TFC+TVC (TFC-фиксированные издержки ,TVC-переменные издержки)

Найдём цену единицы продукции:

20p=100 – Q p=5 – Q/20.

Тогда

П=(5 – Q/20)Q – (50 + 2Q)= – Q² + 60Q - 1000

Найдём производную: П'(Q)= –2Q+60.

Приравняем производную к нулю: –2Q+60=0 Q=30.

При переходе через точку Q=30 функция П(Q) меняет свой знак с плюса на минус, следовательно, эта точка является точкой максимума, и в ней функция прибыли достигает своего максимального значения. Таким образом, объём выпуска, максимизирующий прибыль, равен 30 единицам продукции.

Применение производной в практической деятельности

Геодезия.

При изучении геометрии мы встречаемся со способом определения высоты предмета с помощью угломерных инструментов. При топографических съемках местности аналогичный прием используется для определения превышения одной точки земной поверхности над другой. Этот способ дает хороший результат, если рассматриваемые точки находятся на незначительном расстоянии. В противном случае начинает сказываться кривизна Земли и возникает существенная погрешность.

Если расстояние между точками В и С достаточно велико, то к найденному (с помощью угломерных инструментов) значению превышения точки В над точкой С прибавляют так называемую поправку на кривизну Земли:

, где R – радиус Земли, l — длина горизонтальной проекции BC.

Пример

Объясните происхождение указанной выше формулы для поправки h.

Решение

Рис. 1

Рассмотрим рис. 1, на котором штрихами изображена поверхность океана, точка О – центр Земли. Пусть, для простоты, точка С лежит на поверхности океана, а точка В принадлежит горизонтальной плоскости, проходящей через точку С. Так как в таком случае угол между лучом СВ и горизонтальным направлением (оно определяется с помощью отвеса) равен нулю, то из точки С нам покажется, что точки В и С имеют одинаковую высоту. Согласившись с этим, мы допустим погрешность: ∆h = АВ = ОВ – О А = – R.

Величина l относительно мала по сравнению с R. Поэтому для вычисления можно воспользоваться приближенной формулой , полученной в курсе "Алгебра и начала анализа 10–11" автор А.Н. Колмогоров. Положив в этой формуле x₀ = R², х = l ², мы получим

∆h = – R +

где R – радиус Земли, l – длина горизонтальной проекции отрезка ВС.

Транспорт.

В практике проектирования сети автомобильных дорог часто возникает необходимость устройства узла разветвления. Местоположение узла и взаимное расположение проходящих через него дорог определяется комплексом экономических и географических условий, но первый, предварительный этап решения этой задачи учитывает лишь затраты рабочего времени на перевозки, причем в качестве вспомогательной решается вначале следующая задача.

Пример

Каким должен быть угол примыкания (рис. 2) дороги СЕ к автомагистрали АВ, чтобы затраты времени на перевозки по маршруту AEC были наименьшими, если скорость движения автомобилей по магистрали планируется равной V_m, а по подъездной дороге – Va(V_m > Va).

Рис. 2

Проведем из точки С перпендикуляр к прямой АВ и обозначим длину отрезка CD через h, а длину отрезка AD через l. Тогда получим:

СЕ = , DE = h • ctg

Отсюда находим время движения автомобиля по маршруту AEC:

Так как точка А в наших рассуждениях зафиксирована условно, определяя лишь направление движения по магистрали, то может изменяться в промежутке (0; ).

Задача свелась к отысканию наименьшего значения функции t( ) на указанном промежутке.

Найдем производную: t'( ) = ( ).

Так как 0 < < 1, то производная на рассматриваемом промежутке обращается в нуль лишь в одной точке

₀ = arccos ,      (1).

Причем t'( ) < 0 при (0; ) и t'( ) > 0 при ( ; ).

Это означает, что на промежутке (0; ₀] функция t убывает, а на промежутке [ ; ) – возрастает. Следовательно, рассматриваемая функция t при = достигает наименьшего значения.

Ответ: угол примыкания определяется по формуле = arccos

Мелиорация.

Площадь поперечного сечения канала (целиком заполнен водой) называют его живым сечением, а длину X границы такого сечения называют смоченным периметром канала. С помощью теоретических расчетов и эксперимента установлено, что из всех каналов с заданным живым сечением наибольшей пропускной способностью и одновременно наименьшей фильтрацией отличаются каналы с наименьшим смоченным периметром. Про такие каналы говорят, что они имеют гидравлически наивыгоднейший профиль.

В мелиоративной практике часто сооружаются каналы или лотки с поперечным сечением в форме прямоугольника, треугольника, трапеции и сегмента круга. Поэтому представляет интерес расчет гидравлически наивыгоднейшего профиля для каналов такой формы.

Пример

При каком отношении глубины к ширине канал прямоугольного сечения имеет гидравлически наивыгоднейший профиль?

Решение

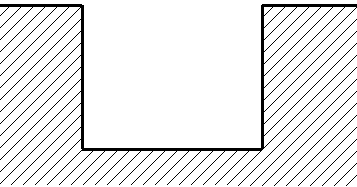
Рис. 3

Пусть х – ширина канала, - его живое сечение. Тогда глубина канала , а его смоченный периметр ( рис. 3 ) : X(x) = x + , X'(x) =

Так как Х'( ) = 0, Х'(х) < 0 при 0 < х < и X'(х) >0 при х > , то функция X в точке достигает наименьшего значения.

Итак, ширина канала в рассматриваемом случае должна быть , глубина

Ответ : .

Строительство.

При монтаже промышленных и сельскохозяйственных зданий небольшой высоты широко используются автомобильные краны. Для правильного выбора крана необходимо знать многие исходные данные о сооружаемом объекте. В частности, габаритные данные объекта позволяют заранее определить требуемую длину стрелы крана. Рассмотрим эту задачу

Пример

Вывести формулу для определения длины стрелы автомобильного крана, с помощью которого можно построить здание высоты Н и ширины 2 c плоской крышей.

Решение

Так как автомобильный кран может перемещаться вокруг всего здания, то крюк его крана достанет до любой точки здания, если он достанет (рис. 4) до середины крыши (имеется в виду середина по ширине).

Рис. 4

Рассмотрим кран, который находится в точке О, подает деталь на середину крыши. Пусть угол наклона стрелы при этом составляет . Тогда BC= = ; AC = = , где h = АО – высота подвеса стрелы крана. В таком случае длина стрелы крана l= + (1)

Из формулы (1) видно, что для совершения указанной работы краном, установленным в другой точке (ближе к зданию или дальше от него), потребуется кран с другой длиной стрелы, поскольку при таком перемещении меняется угол . Определим наивыгоднейшее место установки крана, т.е. такое место, с которого заданная работа может быть выполнена краном с наименьшей длиной стрелы. Для этого, очевидно, достаточно определить, при каком, из промежутка (0; ) функция l принимает наименьшее значение.

Найдем производную функции

Производная обращается в нуль лишь в одной точке = arctg и функция l достигает своего наименьшего значения при = arctg .

Найдя из полученной формулы значение и подставив его в формулу (1), мы и получим наименьшее возможное значение стрелы. Эти формулы и используются на практике.

Деревообработка.

Важное народнохозяйственное значение имеет рациональный раскрой древесины. Комплексное решение таких задач требует применения довольно глубоких методов классической и современной математики. Однако отдельные задачи такого рода можно решить, используя только производную.

Пример

На лесопильных рамах (они предназначены для продольного пиления) бревна часто распиливают на квадратный брус и четыре доски (рис. 5) с максимально возможной площадью поперечного сечения. Какой должна быть расстановка пил для такой распиловки?

Решение

Рис. 5

Из рис. 9 видно, что для ответа на вопрос задачи достаточно определить толщину выпиливаемых досок. Так как сторона квадрата, вписанного в окружность радиуса r, равна r , то ОА = .

Пусть толщина доски АВ = х, тогда ее ширина 2ВС = = , а площадь поперечного сечения:

S(x) = 2 = .

Требуется узнать, при каком х из отрезка [0; ] функция S достигает наибольшего значения.

Найдем производную : S'(x) = .

Критическая точка: x₀= Так как S(0) = S , а S(x₀)' > 0, то доски толщиной 0,10d имеют наибольшую площадь поперечного сечения.

Ответ: 0,10d.

Сельское хозяйство и животноводство.

Усилению политехнической и трудовой направленности обучения математике способствует решение задач практического характера. Многие из этих задач сводятся, как известно, к нахождению наибольшего или наименьшего значения функции на некотором промежутке.

Пример

Пастбищные водопоильные желоба для коров иногда устраивают из трех одинаковых досок, сбивая их под некоторым тупым углом величины . Каким должен быть угол , чтобы получился желоб наибольшей вместимости? (рис. 6)

Рис. 6

Решение

Обозначим через х величину угла BAD, а через h ширину досок, тогда

АВ = ВС = CD = h, AE = h·cosx, AD = h + 2h·cosx, BE = h·sinx.

Желоб представляет собой призму, основанием которой служит трапеция ABCD, а высота равна длине сбиваемых досок. Обозначив длину досок через l, найдем объем желоба. V(x) = l h² (1+cosx)sinx. Требуется узнать при каком значении х из интервала (0; ) функция V принимает наибольшее значение.

Найдем производную функции V:

V' = l h² (cosx·(l + cosx) – sin²x) = l ·h² (2cos²x + cosx – 1) =

2 l h² (cosx – )· (cosx +1),

замечаем, что на рассматриваемом интервале производная существует и обращается в нуль только при х = , причем при 0 < х < производная положительна, а при < х < отрицательна. Значит, функция V достигает своего наибольшего значения на интервале (0; ) при х = .

Зная оптимальное значение x, найдем искомое значение : .

Ответ:

Пример

Каким должно быть отношение диаметра основания к высоте закрытой цилиндрической цистерны, чтобы при заданном объеме на изготовление цистерны шло как можно меньше материала?

Решение

Пусть r – радиус основания, V – объем цистерны, тогда ее высота равна , а полная поверхность S(r) = 2( г² + ). Требуется узнать, при каком r из промежутка (0;+ ), функция S достигает наименьшего значения.

Найдем производную: S' (r) = 2·(2 = ).

Замечаем, что производная всюду на рассматриваемом интервале существует и обращается в нуль только в точке, = причем S'(r) < 0 при 0 < < и S'(x) > 0 при > .

Функция S при r = r₀ достигает наименьшего значения. При величине радиуса г = г₀ высота цистерны h₀ = = , т.е. высота цилиндра должна быть равна его диаметру, а отношение равно 1.

Ответ: 1.

Защита

Задача 1

Дан равнобедренный треугольник со сторонами а. Найти наибольшую площадь треугольника.

Запишем формулу для нахождения площади равнобедренного треугольника:

B

Р ассмотрим треугольник АВК,

a a

A K C

Из данной формулы выведем несколько значений, которые в дальнейшем нам помогут в решении задачи :

1.

2.

Произведем несколько элементарных преобразований.

По формуле половинного угла

, тогда получаем

Исследуем функцию на экстремум:

	( 0, )		( )
	+	0	-

Воспользуемся первым достаточным условием экстремума функции:

Пусть x_о - критическая точка. Если f ( x ) при переходе через точку x_о меняет знак плюс на минус, то в точке x_о функция имеет максимум, в противном случае - минимум.

Вывод: наибольшая площадь треугольника будет достигаться тогда, когда угол будет равен

Задача 2

Что больше:

Преобразуем:

Введем функцию:

Найдем производную функции:

F’(x )=

x=e

на заданном точками интервале функции найдем экстремум,что будет и ответом

x	( 0,e )	[ e ]	(e;+ )
f (x)	+	0	-
f(x)

В ывод: точка e является точкой локального максимума на всем промежутке (0;+∞),отсюда сделаем вывод, так как > e,что равносильно _,

следовательно .

Задача 3

Аналогично предыдущему заданию сравним величины:

Что больше?

Введем функцию

F’(x) =

x=e

Найдем промежутки возрастания и убывания функции f

x	( 0,e )	[ e ]	(e;+ )
f (x)		0
f(x)

Ответ: так как 100 и 101∊ (0;+∞) и функция строго убывает на этом интервале и 100<101, то отсюда следует, что:

это равносильно ,

следовательно .

Заключение

Дифференциальное исчисление - это описание окружающего нас мира, выполненное на математическом языке. Производная помогает нам успешно решать не только математические задачи, но и задачи практического характера в разных областях науки и техники.

В наше время, в связь с научно-техническим прогрессом, в частности с быстрой эволюцией вычислительных систем, дифференциальное исчисление становиться всё более актуальными в решении как простых, так и сверхсложных задач.

Применение производной довольно широко, и его можно полностью охватить в работе такого типа, однако я попыталась раскрыть основные базовые моменты.

Мы убедились в важности изучения темы "Производная", ее роли в исследовании процессов науки и техники, в возможности конструирования по реальным событиям математические модели, и решать важные задачи.

Литература

[1]- Кудрявцев Л.Д, «Курс математического анализа»/Л.Д.Кудрявцев-1998.

[2]- Фихтенгольц Г.М, «Основы математического анализа»/Г.М Фихтенгольц-1999

[3]- Бохан К.А, «Курс математического анализа» / К.А Бохан- «Просвещение»,1972

[4]- Петров В.А, «Математический анализ в производственных задачах» / В.А Петров- «Просвещение»,1990