Вираз фокальних радіусів точки гіперболи

Директриса гіперболи. Теорема про фокальні властивості гіперболи

Директрисами гіперболи називаються прямі, які перпендикулярні до фокальної осі гіперболи і лежать на відстані від центра гіперболи.

Рівняння директрис гіперболи (13.1.2) мають вигляд

Оскільки то директриси гіперболу не перетинають.

Теорема 13.6.1 (про фокальну властивість гіперболи). Відношення фокальних радіусів цієї точки до відповідних директрис є величина стала і дорівнює ексцентриситету гіперболи:

(13.6.1)

Мал. 13.6.1

Нехай у — це гіпербола (див. мал. 13.6.1), яка мас ексцентриситет с задається канонічним рівнянням:

Її директриси:

і

а фокуси - і

Не порушуючи загальності, нехай - точка кривої , яка належить першій чверті.

Міркуючи аналогічно (як і для еліпса), маємо:

і

Звідки

(13.6.2)

. (13.6.3)

Виражаємо

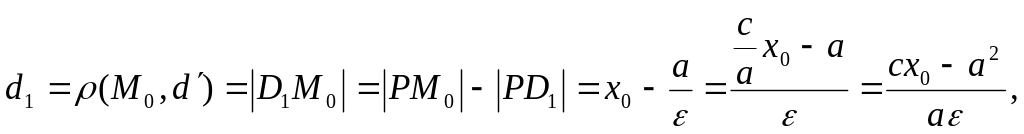(13.6.4)

(13.6.5)

Підставляючи (13.6.2) і (13.6.3) в (13.6.4) і (13.6.5), отримуємо

і

Виразивши з цих рівностей , отримаємо рівність (13.6.1) для гіперболи.

Теорему доведено.

Побудова точок гіперболи за допомогою циркуля та лінійки

Розглянемо спосіб побудови точок гіперболи, якщо вона задана фокусами та і дійсною віссю

Нехай - коло з центром і довільним радіусом - коло з центром і довільним радіусом Тоді, згідно з означенням, точка належить гіперболі з дійсною віссю і фокусною відстанню

Б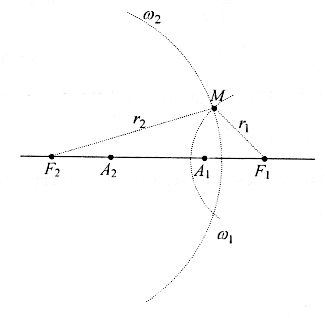 еручи різні значення , ми отримуємо різні значення точки тієї ж вітки гіперболи.

Якщо довільним брати радіус , а , то отримаємо точки іншої вітки гіперболи.

Отже, для побудови гіперболи досить побудувати кола і . Обидві їх точки перетину належать гіперболі.

Дотична до гіперболи

Теорема 1. Дотична до гіперболи в точці задається рівнянням

Доведення. Оскільки пряма проходить через точку :

І має вектор напрямку то її параметричні рівняння мають вигляд:

Доведемо, що пряма з гіперболою має лише одну спільну точку (точніше: дві співпадаючі). Для цього розглянемо систему:

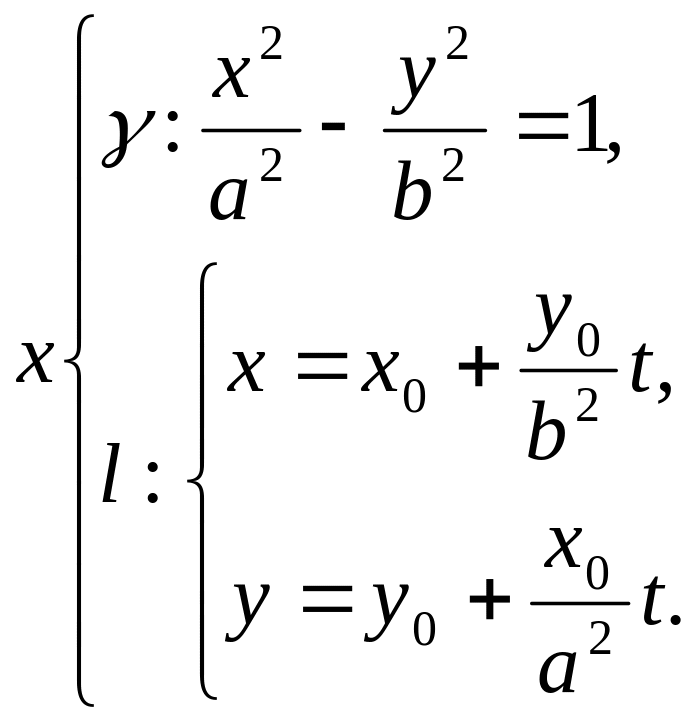
Після підстановки в перше рівняння двох інших виразів отримаємо:

Звідки:

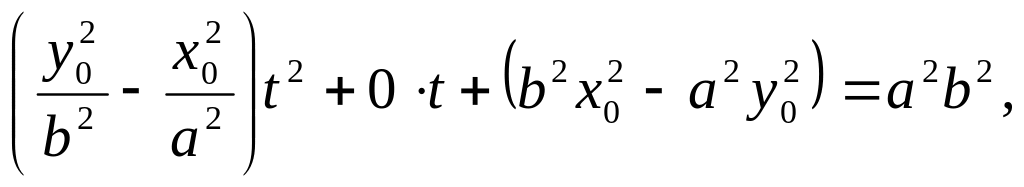тобто

Отже, пряма з гіперболою має лише одну спільну точку

Оптичні властивості гіперболи. Теорема про оптичну властивість гіперболи.

Теорема 13.9.1. Дотична до гіперболи утворює однакові кути з фокальними радіусами точки дотику.

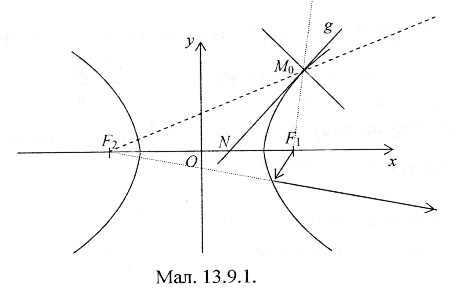
Доведення. Враховуючи симетрії гіперболи, міркування досить провести для точки дотику, яка належить першій координатній чверті .

Нехай в прямокутній Декартовій системі координат гіпербола задана канонічним рівнянням

Дотична до в точці записується рівнянням

Знайдемо точку перетину з віссю

Тоді

і

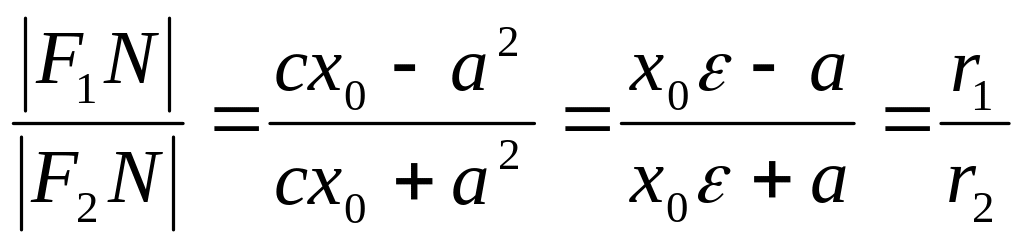
Використовуючи відому з шкільного курсу властивість бісектриси кута трикутника, робимо висновок, що відрізок є бісектрисою трикутника що й вимагалось довести.

Фізичний зміст оптичної властивості гіперболи: всі промені, що виходять з одного фокуса при дзеркальному відбиванні від гіперболи здаються такими, що виходять з іншого фокуса (див. мал. 13.9.1).