Змістовий модуль 6. Поверхні другого порядку. Загальна теорія поверхонь другого порядку. Геометричні перетворення простору.

Лекція № 15. Поверхні іі порядку. Циліндричні і конічні поверхні. Прямолінійні твірні поверхонь іі порядку.

Циліндричні поверхні

Означення 4.1. Поверхня, утворена внаслідок руху прямої, яка перетинає задану криву і залишається паралельною даній прямій, називається циліндричною поверхнею.

Прямі, які повністю лежать на цій поверхні і паралельні заданій прямій, називаються твірними циліндричної поверхні, а крива L, яку перетинають ці твірні, називається напрямною цієї поверхні (рис. 7).

П рипустимо, що напрямна крива циліндричної поверхні розміщена в деякій площині, а твірні циліндричної поверхні перпендикулярні до цієї площини. Введемо прямокутну систему координат так, щоб напрямна крива L містилась у площині ОХY, а твірні були паралельні до осі 0Z (рис. 8)

Рис. 7

Припустимо, що крива L у плоскій системі координат ОХY задана рівнянням

F(х; y) = 0. (9)

Н ехай М(х; у; z) — довільна точка циліндричної поверхні, тоді її проекція на площину ОХY М'(х; у; 0) лежить на кривій L. Тому F(х; у) = 0. Отже, координати довільної точки М циліндричної поверхні задовольняють рівняння (9).

Якщо ж деяка точка М₁(х₁; у₁; z₁) не лежить на даній циліндричній поверхні, то її проекція на площину ОХY М₁^’(х₁; у₁, 0) не лежить на кривій L і, отже, F(х₁; у₁) ≠ 0.

Таким чином, рівняння (9) задовольняють координати довільної точки циліндричної поверхні і тільки вони, тому це рівняння буде рівнянням даної циліндричної поверхні.

Аналогічно встановлюємо, що коли напрямна крива задана рівнянням F(х; z) = 0 у площині ОХZ, то в просторовій системі координат це рівняння задає циліндричну поверхню, твірні якої паралельні до осі ОY.

Якщо ж крива задана рівнянням F(у; z} = 0 у площині ОYZ, то в просторовій системі координат це рівняння буде рівнянням циліндричної поверхні, твірні якої паралельні до осі ОХ.

У результаті можна дійти такого висновку: якщо в рівнянні поверхні відсутня одна зі змінних, то ця поверхня є циліндром., твірні якого паралельні до тієї координатної осі, змінна якої відсутня в даному рівнянні.

Приклади.

1. Еліптичний циліндр (рис. 9).

Його рівняння

Н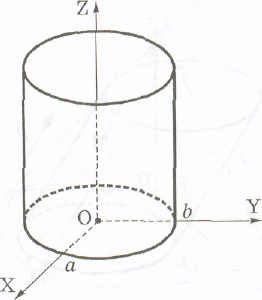 апрямною є еліпс з півосями а і b.

2. Гіперболічний циліндр (рис. 10).

Рівняння

Напрямною є гіпербола з дійсною піввіссю a і уявною піввіссю b.

Рис. 9

3. Параболічний циліндр (рис. 11).

Його рівняння у² = 2рх.

Напрямною є парабола.

На прикладі покажемо, як можна знайти рівняння циліндричної поверхні, твірні якої мають довільний напрям.

Приклад. Скласти рівняння циліндричної поверхні, напрямна якої лежить в площині OXY і має рівняння х² + 2ху + 3у² - х = 0, а твірні паралельні вектору р(1; 0; 1).

Розв'язання. Рівняння напрямної L у просторі матиме вигляд:

(10)

Рис. 10

Н ехай М (х; у; z) - довільна точка циліндричної поверхні. Проведемо через неї твірну MM', де М' точка перетину цієї твірної з площиною OXY, а отже, - і з напрямною L (рис. 12). Нехай координати точки М'(х';у'; 0). Оскільки М' є L, то її координати задовольняють рівняння (10), тому

х ^΄2 + 2х΄у΄ + Зy΄² - х΄ = 0. (11)

Рис.11

Запишемо параметричні рівняння твірної MM', заданої точкою М'(х', у', 0) і напрямним вектором P(1;0;1)

(12)

Змінні (х; у; z) в цьому рівнянні є координатами точок твірної, а отже, й координатами точок циліндричної поверхні. Координати точки М'(х'; у'; 0) задовольняють рівняння (11) і (12).

Тому, виключаючи х', у', z' з рівнянь (11) і (12), дістаємо співвідношення між координатами точок циліндра, тобто рівняння циліндра.

Рис.12 Маємо:

Отже, рівняння даної циліндричної поверхні. (х – z)²+ 2(х - z)y + Зу² - (х - z) = 0.