П.2. Случайная погрешность.

Случайная составляющая погрешности измерений определяется принципом действия, конструкцией, схемой и характеристиками измери­тельного средства, случайными процессами в контролируемом объекте и ок­ружающей среде, ее источником могут быть также условия эксплуатации, действия персонала, производящего измерения, и другие случайные при­чины. Способы расчета величины случайной погрешности измерений осно­вываются на методах математической статистики.

Предполагается, что каждому из источников случайной погрешности соответствует свой закон распределения вероятности возникновения опреде­ленной величины погрешности. На практике обычно рассматривают некое приближение к реальному закону распределения, наиболее простому для анализа и расчетов. В случае технических измерений в качестве такого при­ближения (аппроксимации) обычно используют либо закон нормального рас­пределения, либо закон равномерного распределения, который хорошо опи­сывает погрешности аналоговых стрелочных и самопишущих приборов, а также треугольный закон распределения, распространенный среди цифровых приборов.

П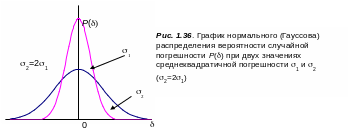 .2.1. Свойства нормального распределения.

Случайная погрешность измерений наиболее часто описы­ваются зако­ном нормального распределения.

С точки зрения процесса измерений:

• нормальное распределение погрешностей есть результат одно­временном действия большого числа независимых факторов, каждый из которых незначительно и независимо от других ока­зывает в влияние на суммарную погрешность измерений.

С точки зрения математической ста­тистике и теории вероятности:

• нормальное распределение есть распределение вероятности суммы независимых случайных величин с конечными диспер­сиями при неограниченном увеличении числа слагаемых

Дисперсия есть среднеквадратичное отклонение измеряемой величины от ее истинного значения и равна:

В реальности мы всегда имеем дело с ограниченным числом источни­ков погрешностей. Однако, при сложении даже только четырех-пяти случай­ных величин с различными законами распределения, но с соизмеримыми дисперсиями (т.е. со сравнимыми величинами погрешностей), мы приходим к закону распределения погрешностей, близкому к нормальному. Особенно, если плотность вероятности достаточно велика

Нормальное распределение плотности вероятности p() центрирован­ной случайной погрешности  описывается функцией Гаусса:

(1.4)

Где:  - величина случайной погрешности, p() – вероятность того, что слу­чайная погрешность окажется равной именно , параметр  называется среднеквадратическим отклонение измеряемой величины от истинной.

Графики нормального распределения вероятности при двух  значениях приведены на рис.1.6. Из формулы Гаусса следует:

• Функция p() четная, т.е. симметрична относительно оси ординат.

• С увеличение  максимальное значение p() уменьшается, кривая расширя­ется, становится более пологой.

• Площадь, ограниченная графиком и осью абсцисс, всегда остается неизмен­ной и равной 1 при любых значениях , что соответствует тому, что вероятность появления ошибки, отличной от нуля равна р(0)=1:

(1.5)

• вероятность того, что погрешность окажется в интервале от =- до =+а, определяется соотношением:

(1.6)

Если принять, что  = t, где t – безразмерный коэффициент, т.е. по сути связать величину погрешности = со среднеквадратичным отклоне­нием, то интеграл ( ) можно преобразовать к виду, который определяет веро­ятность нахождения величины погрешности в интервале =t и называется интегралом ошибок:

(1.7)

Значения интеграла ошибок Ф(t) заранее вычислены, затабулированы и широко используются в практических расчетах: