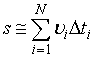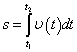1. Средняя и мгновенная скорость материальной точки

Средней скоростью называется физическая величина равная отношению изменения координаты точки к интервалу времени, в течение которого это изменение произошло.

Пусть за интервал времени от t₀ до t₁ координата точки изменилась от x₀ до x₁. Если мы вычислим скорость по прежнему правилу

, (1)

то получим величину (она называется средней скоростью), которая описывает быстроту движения «в среднем» - вполне возможно, что за первую половину времени движения точка сместилась на большее расстояние, чем за вторую.

Мгновенной скоростью называется отношение изменения координаты точки к интервалу времени, за которое это изменение произошло, при интервале времени, стремящемся к нулю ^[1]:

, при Δt → 0 .

2. Вычисление пройденного пути

Из выражения (3.5) следует, что при малых ∆t

(4.1)

Последнее приближенное равенство выполняется тем точнее, чем меньше ∆t. Если известна величина скорости v как функция времени t, можно вычислить путь, пройденный точкой с момента t1 до момента t₂. Для этого разобьем промежуток времени t₁-t₂ на N малых промежутков: ∆t₁, ∆t₂, …, ∆t_N, которые могут быть различными по величине. Весь путь s, пройденный точкой, можно представить как сумму путей: ∆s₁, ∆s₂, …, ∆s_N пройденных за соответствующие промежутки времени ∆t;

[1]

В соответствии с (4.1) каждое из слагаемых ∆s_і (і — любое число от 1 до N) может быть приближенно представлено в виде

где ∆t_і — промежуток времени, за который был пройден ∆s_і, a v_i — одно из значений скорости за время ∆t_і. Таким образом,

(4.2)

Написанное равенство выполняется тем точнее, чем меньше промежутки времени. В пределе при стремлении всех ∆t_і к нулю (количество промежутков ∆t_і будет при этом неограниченно возрастать) сумма, стоящая справа, станет точно равна s:

(4.3)

Скорость есть функция времени: υ=υ(t). В математике выражения вида:

составленное для значений х, заключенных в пределах от а до b, называют определенным интегралом и записывают символически следующим образом;

Следовательно, путь, пройденный точкой за промежуток времени от t₁ до t₂ равен определенному интегралу

(4.4)

Покажем, что величину пройденного пути можно представить как площадь фигуры, которая ограничена кривой зависимости величины скорости v от времени t. Построим график функции v=v(t) (рис. 22). Произведение υ_і∆t_і численно равно площади заштрихованной (і-й) полоски. Сумма таких произведений будет равна площади, ограниченной осью t прямыми t=t₁ и t=t₂, а также ломаной линией, образованной верхними краями

всех подобных полосок. При стремлении ∆t_і к нулю ширина всех полосок убывает (одновременно число их растет) и ломаная линия в пределе сольется с кривой

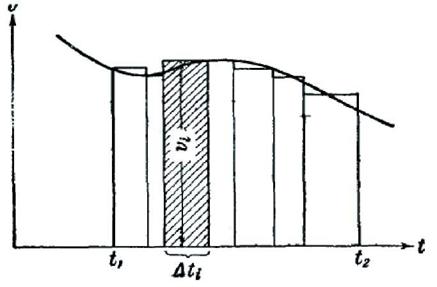
Рис.22

Таким образом, путь, пройденный за время с момента t₁ до момента t₂ численно равен площади фигуры, ограниченной графиком υ=υ(t), осью времени t и прямыми t=t₁ и t=t₂.

 

3. Тангенциальное, нормальное и полное ускорение точки

Тангенциа́льное ускоре́ние  — компонента ускорения, направленная по касательной к траектории движения. Совпадает с направлением вектора скорости при ускоренном движении и противоположно направлено при замедленном. Характеризует изменение модуля скорости. Обозначается обычно или ( , итд в соответствии с тем, какая буква выбрана для обозначения ускорения вообще в данном тексте).

Величину тангенциального ускорения - в смысле проекции вектора ускорения на единичный касательный вектор траектории - можно выразить так:

где - путевая скорость вдоль траектории, совпадающая с абсолютной величиной мгновенной скорости в данный момент.

Если использовать для единичного касательного вектора обозначение , то можно записать тангенциальное ускорение в векторном виде:

Центростремительное ускорение — часть полного ускорения точки, обусловленного кривизной траектории и скоростью движения по ней материальной точки. Такое ускорение направлено к центру кривизны траектории, чем и обусловлен термин. Формально и по существу термин центростремительное ускорение в целом совпадает с термином нормальное ускорение.

или

где  — нормальное (центростремительное) ускорение,  — (мгновенная) линейная скорость движения по траектории,  — (мгновенная) угловая скорость этого движения относительно центра кривизны траектории,  — радиус кривизны траектории в данной точке. (Cвязь между первой формулой и второй очевидна, учитывая ).

Выражения выше включают абсолютные величины. Их легко записать в векторном виде, домножив на  — единичный вектор от центра кривизны траектории к данной ее точки:

Эти формулы равно применимы к случаю движения с постоянной (по абсолютной величине) скоростью, так и к произвольному случаю.

Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:

(согласно теореме Пифагора для прямоугольно прямоугольника).

Направление полного ускорения также определяется правилом сложения векторов:

= _τ + _n