Раздел 7

Математическое моделирование, как основной метод исследования энергетических КА на начальном этапе проектирования

Вопрос 2 Математические модели и их классификация

При математическом моделировании исследуются математиче­ские зависимости, описывающие явление, взамен изучения и исследования оригинала.

Математическая модель должна строиться для решения кон­кретной задачи исследования. В зависимости от цели исследования те или иные связи и стороны явления могут оказаться основными или второсте­пенными.

В математической форме математическая модель может быть пред-­ ставлена следующим образом:

где F-- выбранный показатель качества системы; - оператор це­левой функции; - информация, вводимая в модель, которая не может изме­ниться по воле исследователя; - управляющие параметры, которые вы­бираются в процессе решения задачи; - оператор ограничений.

Математическая модель реальной системы является абстрактным, формально описанным объектом, изучение которого возможно математи­ческими методами.

Сложность и многообразие процессов функционирования реальных систем не позволяют строить для них абсолютно адекватные математиче­ские модели. Формализованная математическая модель отображает лишь наиболее существенные закономерности изучаемого процесса или системы, оставляя в стороне второстепенные задачи.

Сложность реальных систем может сильно затруднить представление цели и ограничений в аналитическом виде. Поэтому очень важно умень­шить «размерность» решаемой задачи таким образом, чтобы обеспечить возможность построения подходящей модели. Несмотря на слишком боль­шое число переменных и ограничений, которые на первый взляд необхо­димо учитывать при анализе реальных ситуаций, лишь небольшая их часть оказывается существенной для описания поведения исследуемых систем.

Поэтому при упрощенном описании реальных систем, на основе ко­торого будет строиться та или иная модель, прежде всего следует иденти­фицировать (селектировать) доминирующие переменные, параметры и ограничения.

Изобразим схематические уровни абстракции, соответствующие пе­реходу от системы-оригинала к ее модели.

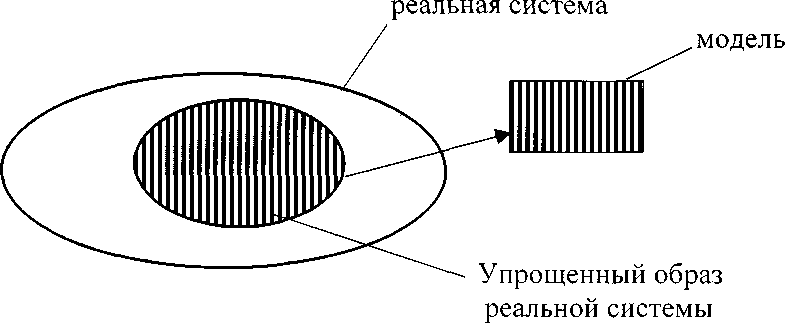
Рис. 2.3. Уровни абстракции при переходе от системы-оригинала к ее модели

Упрощенный образ реальной системы отличается от системы-оригинала тем, что в нем находят отражение только доминирующие фак­торы (переменные, ограничения и параметры), определяющие основную линию поведения реальной системы. Модель, будучи дальнейшим упро­щением образа системы-оригинала, представляет собой наиболее существенные для описания системы соотношения в виде целевой функции и со­вокупности ограничений.

Правил, определяющих переход от реальной системы к модели, не существует. Сведение множества факторов, управляющих поведением сис­темы, к относительно небольшому количеству доминирующих факторов и переход от упрощенного образа системы-оригинала к модели - в большей мере искусство, чем наука. Степень адекватности построенной модели ре­альной системе зависит прежде всего от творческих способностей и интуи­ции членов исследовательской группы. Ясно, что проявление этих чисто индивидуальных качеств нельзя отразить в рамках формализованных пра­вил построения моделей.

К основным признакам классификации математических моделей следует отнести: 1) форму операторов и ;

2) характер учета времени;

3) наличие или отсутствие случайных факторов;

4) степень адекватности реальной системе;

5) возможности и методы исследования математических моделей;

6) характер этапа жизнедеятельности системы;

7) цель исследования системы.

По форме операторов и математические модели разделяют на:

1) аналитические и статистические;

2) линейные и нелинейные;

3) с ограничениями и без ограничений.

В аналитических моделях показатель качества связывается с вели­чинами и аналитическими зависимостями. В статистических моде­лях показатель качества можно вычислить только для конкретных значе­ний величин и (их случайных реализаций). Математическое ожидание и в общем случае функция распределения показателя качества вычисляют­ся статистической обработкой значений показателя, найденных для ряда случайных реализаций величин и .

Если целевая функция F и ограни­чения линейны, то есть, если, например, их можно записать в следующем виде

,

где - исходные данные, то модель является линейной.

Если же целевая функция F или ограничения нелинейны относительно

управляющих параметров , то математическая модель относится к классу нелинейных.

В зависимости от наличия или отсутствия ограничений, наклады­ваемых на значения управляющих параметров, математические модели можно разделить на два вида: с ограничениями и без ограничений.

По характеру учета времени математические модели можно разде­лить на статические, кинематические и динамические.

В статических моделях не учитывается изменение характеристик системы во времени. Статическая модель описывает связь между компонентами состояния или между этими компонентами и другими характеристиками системы в условиях равновесия и других условиях «заморажива­ния» изменения состояния.

Динамической называется модель, в которой в той или иной форме раскрываются причинно-следственные связи, определяющие развивающийся во времени процесс перехода системы из одного состояния в дру­гое.

Кинематической моделью называется модель динамической систе­мы, описывающая изменение состояния как функции времени и не раскры­вающая причинно-следственные связи, вызывающие это изменение.

Из перечисленных выше моделей наибольшими потенциальными возможностями адекватного отражения свойств реальных систем обладают динамические модели.

В зависимости от наличия или отсутствия случайных факторов ма­тематические модели можно разделить на:

детерминированные;

вероятностные (стохастические); теоретико-игровые.

Детерминированная модель строится в тех случаях, когда исходные факторы ( ), влияющие на принятый показатель качества и определяющие ограничения модели, поддаются точной оценке, а случайные факторы либо отсутствуют, либо ими можно пренебречь.

В стохастических моделях исходная информация ( ) описывается теми или иными характеристиками случайных величин: математическим ожиданием, дисперсией, функцией распределения и др. Построение таких моделей возможно, если имеется достаточный фактический материал для описания вероятностных распределений.

В теоретико-игровых моделях учитываются недостаточность ис­ходной информации и необходимость принимать решения в условиях не­определенности. Исследуются такие модели на базе теории игр. Теоретико-игровой подход по существу состоит в том, что выявляется наименее бла­гоприятное распределение значений неуправляемых переменных и нахо­дится оптимальное решение в этих наименее благоприятных условиях.

Как уже упоминалось в предыдущей лекции, по степени соответствия реальной системе математические модели разделяются на изоморфные и гомоморфные.

Математическая модель, которая включает в себя все черты, теорети­чески присущие данной реальной системе, называется изомофной (струк­турный, элементный и поведенческий изоморфизм). Достаточно очевидно, что в тех случаях, когда исследуемая система очень сложна, создание изо­морфной модели невозможно. Однако, к счастью, для практических целей, в этом нет необходимости. Может случиться, что иногда будет более эф­фективно рассмотрение некоторых упрощенных вариантов модели реаль­ной системы, чем попытка создания детализированной совершенной моде­ли.

Во многих ситуациях оказывается необходимым и удобным объеди­нить при моделировании связанные переменные в одну, принимать некото­рые достаточно широкие и общие предположения, пытаясь получить на модели некоторые общие черты поведения рассматриваемой системы (гомоморфная модель) , а не ее детальное поведение. Все это облегчает создание модели и осмысление полученных результатов.

Один из самых главных вопросов, возникающих при применении не­изоморфных моделей, состоит в выборе уровня гомоморфизма, то есть уровня приближения к действительности, при котором еще возможно дос­тижение желаемых результатов.

По возможностям и методам исследования математические моде­ли разделяются на:

1. модели, исследуемые аналитическими методами;

2. модели, для исследования которых применяются численные мето­ды;

3) модели, для исследования которых используется метод Монте-Карло (метод статистических испытаний).

По характеру этапа жизнедеятельности системы математиче­ские модели могут быть моделями проектирования системы, моделями эксплуатации системы, моделями применения системы по назначению и так далее.

По цели исследования системы математические модели можно раз­делить на модели 1) анализа процесса функционирования системы и 2) оптими­зационные модели.