6. Система n линейных уравнений с n переменными (общий вид).

Системой n линейных уравнений с n переменными называется система вида:

,

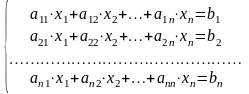Где a_ij (i=1,2,...,n; j=1,2,...,n) - коэффициенты при переменных;b_i (i=1,2,...,n) - свободные члены. Запишем систему линейных уравнений в матричной форме..Имеем 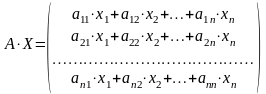- матрица-столбец. Следовательно, по определению равенства матриц, систему уравнений можно записать в виде AX=B , где A - матрица коэффициентов при переменных, Х - матрица столбец переменных, B - матрица-столбец свободных членов.

 Решением системы уравнений называется такой упорядоченный набор (k₁, k₂, ... , k_n) чисел, при подстановке которых вместо переменных x₁, x₂, ... , x_n каждое уравнение системы обращается в верное числовое равенство.

 Система уравнений называется совместной, если она имеет хотя бы одно решение.

 Система уравнений называется несовместной, если она не имеет решений.

 Совместная система уравнений называется определенной, если она имеет единственное решение.

Совместная система уравнений называется неопределенной, если она имеет более одного решения.

 Две системы уравнений называются равносильными или эквивалентными, если они имеют одно и то же множество решений

7. Решение системы n линейных уравнений с n переменными по формулам Крамера

Пусть дана система двух линейных уравнений с двумя переменными:

.

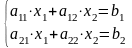Умножим первое уравнение на a₂₂, второе уравнение на (-a₁₂) и сложим их. Получим уравнение (a₁₁a₂₂-a₂₁a₁₂)x₁=b₁a₂₂-b₂a₁₂ .

Умножим первое уравнение на (-a₂₁), второе уравнение на a₁₁ и сложим их. Получим уравнение (a₁₁a₂₂-a₂₁a₁₂)x₂=a₁₁b₂-a₂₁b₁.

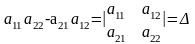
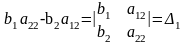
Заметим,что 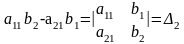т.е. система имеет вид .

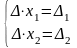Если 0, то система имеет единственное решение , .

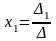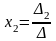Если =0, а ₁0 или ₂0 то система несовместная.

Если =0, ₁=0 и ₂=0 , то система неопределенная и имеет бесконечное множество решений.

Теорема Крамера. Пусть  - определитель матрицы A системы n линейных уравнений с n переменными, _j - определитель матрицы, полученной из матрицы A заменой j-го столбца столбцом свободных членов (j=1,2,...,n). Тогда, если 0, то система имеет единственное решение, определяемое по формулам , , . . . , 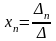(формулы Крамера).

8. Решение системы n линейных уравнений с n переменными

с помощью обратной матрицы (вывод формулы X=A^-1B)

В матричной форме система n линейных уравнений с n переменными записывается в виде AХ=B..

Если A0, то существует обратная матрица А^-1. Умножая слева обе части матричного равенства AХ=B на матрицу А^-1, получим А^-1(АХ)=А^-1В. Но А^-1(АХ)= (А^-1А)Х=ЕХ=Х.

Следовательно, решением системы n линейных уравнений с n переменными методом обратной матрицы является матрица-столбец А^-1В.

9. Метод Гаусса решения системы n линейных уравнений с n переменными. Понятие о методе Жордана-Гаусса

Метод Гаусса - метод последовательного исключения переменных - заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последней переменной, находятся все остальные переменные.

Пусть дана система n линейных уравнений с n переменными:

(1) .

Шаг 1. Предположим, что a₁₁0. Умножаем первое уравнение на 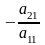, прибавляем его ко второму уравнению. Аналогично исключаем переменную x₁ из остальных уравнений:

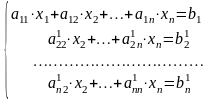(2) .

Шаг 2. Предположим, что a₂₂0. Исключаем переменную x₂ из всех уравнений, начиная с третьего.

После (n-1)-го шага получаем систему треугольного вида

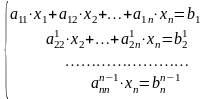(n) .

Переход от системы (1) к равносильной системе (n) называется прямым ходом метода Гаусса.

Если 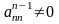, то .

Далее, если 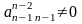, то 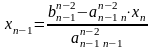. Продолжая, находим все остальные переменные. Нахождение переменных из системы (n) называется обратным ходом метода Гаусса.

Замечание. Преобразования Гаусса удобно проводить не с самими уравнениями, а с матрицей их коэффициентов

,

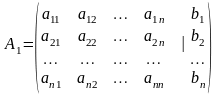называемой расширенной матрицей системы (1)

10. Система m линейных уравнений с n переменными. Теорема Кронекера-Капелли. Условия определенности и неопределенности совместной системы линейных уравнений

Пусть дана система m линейных уравнений с n переменными:

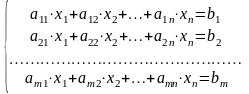. Теорема Кронекера-Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы.

Для совместных систем линейных уравнений верны следующие теоремы:

1. Если ранг матрицы совместной системы равен числу переменных, то система имеет единственное решение.

2. Если ранг матрицы совместной системы меньше числа переменных, то система имеет бесконечное множество решений.

Замечание. На практике обычно производят (методом Гаусса) преобразования расширенной матрицы системы, что позволяет одновременно решить вопрос о совместности и определенности системы линейных уравнений

11. Базисные (основные) и свободные (неосновные) переменные системы m линейных уравнений с n переменными. Базисное решение

Пусть r < n. r переменных x₁, x₂, ... , x_r называются основными (базисными), если определитель матрицы из коэффициентов при них отличен от нуля. Остальные n - r переменных называются неосновными (свободными).

 Решение системы m линейных уравнений с n переменными, в котором все n - r неосновных переменных равны нулю, называется базисным.

Заметим, что совместная система m линейных уравнений с n переменными (m < n) имеет бесконечное множество решений, среди которых базисных решений конечное число, не превосходящее , где r  m.

12. Система линейных однородных уравнений

Cистома m линейных уравнений с n переменными называется системой линейных однородных уравнений, если все их свободные члены равны нулю

Такая система всегда совместна, так как имеет нулевое решение. Выясним, когда система линейных однородных уравнений имеет ненулевые решения.

Если m = n, а главный определитель системы отличен от нуля, то, по теореме Крамера, система имеет единственное решение, т.е. нулевое решение.

Следовательно, верна теорема

Теорема 1.  Система линейных однородных уравнений имеет ненулевые решения тогда и только тогда, когда ранг ее матрицы при переменных меньше числа переменных, т.е. r(A)<n.