Билет1. Понятие матрицы.

Матрицей размера mn называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.

Две матрицы одного размера mn называются равными, если они совпадают поэлементно, т.е. А=В  a_ij=b_ij для любых i=1,2,...,m; j=1,2,...,n.

.

Матрица называется квадратной матрицей n-го порядка, если число ее строк равно числу ее столбцов и равно n .

Элементы a_ij матрицы A, у которых номер строки i равен номеру столбца j, называются диагональными. Они образуют главную диагональ матрицы.

Квадратная матрица называется диагональной, если все недиагональные элементы равны нулю.

Единичной матрицей n-го порядка называется диагональная матрица n-го порядка, у которой все диагональные элементы равны 1.

Матрица любого размера называется нулевой, если все ее элементы равны 0.

Матрица A’, которая получается из матрицы A заменой строк столбцами, называется транспонированной по отношению к матрице А.

Из определения следует, что если матрица A имеет размер mn, то транспонированная матрица A' имеет размер nm .

Произведением матрицы A на число  называется матрица B=A, элементы которой b_ij=a_ij для любых i=1,2,...,m; j=1,2,...,n .

Суммой двух матриц A и B одного размера называется матрица C=A+B, элементы которой с_ij=a_ij+b_ij для любых i=1,2,...,m; j=1,2,...,n

Если число столбцов матрицы A равно числу строк матрицы B и равно k, то произведением матриц A и B называется матрица C=AB, каждый элемент которой с_ij равен сумме произведений элементов i-ой строки матрицы A на соответствующие элементы j-го столбца матрицы B, т.е. с_ij=a_i1b_1j+a_i2b_2j+...+a_ikb_kj для любых i=1,2,...,m; j=1,2,...,n

Многие свойства операций над числами справедливы и для операций над матрицами (это проверяется по определению операций):

1)A+B=B+A;2)(A+B)+C=A+(B+C);3)(A+B)=A+B;4)A(BC)=(AB)C;5)(AB)=(A)B=A(B);

6) (A+B)C=AC+BC;7) A(B+C)=AB+AC.

Билет2. Определители 2-го и 3-го порядков.

Определителем матрицы 2-го порядка (определителем 2-го порядка) называется число, которое вычисляется по формуле..

 Определителем матрицы 3-го порядка A (определителем 3-го порядка) называется число, которое вычисляется по формуле.Заметим, что определитель 3-го порядка матрицы A есть алгебраическая сумма 3!=6 слагаемых, каждое из которых есть произведение трех множителей, взятых в точности по одному из каждой строки и каждого столбца матрицы А.

Определителем квадратной матрицы n-го порядка A (определителем n-го порядка) называется число, которое вычисляется по формуле, где r(J) - число инверсий в перестановке J из номеров столбцов матрицы (когда номера строк записаны в порядке возрастания), а сумма берется по всем перестановкам J .

Заметим, что определитель n-го порядка матрицы A есть алгебраическая сумма n! слагаемых, каждое из которых есть произведение n множителей, взятых в точности по одному из каждой строки и каждого столбца матрицы А.

Свойства определителей

Позволяют существенно упростить вычисление определителя, особенно для определителей высоких порядков. При этом основной целью преобразований является получение определителя, в котором как можно больше элементов равно нулю.

1. Если какая-либо строка (столбец) матрицы состоит из одних нулей, то ее определитель равен 0,

2. Если все элементы какой-либо строки (столбца) матрицы умножить на число , то ее определитель умножится на это число .

3. При транспонировании матрицы ее определитель не изменяется, т.е. А'=A.

4. При перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.

5. Если квадратная матрица содержит две одинаковые строки (столбца), то ее определитель равен 0.

6. Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен 0.

7. Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна 0.

8. Определитель матрицы не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число.

9. Сумма произведений произвольных чисел b₁, b₂, ..., b_n на алгебраические дополнения элементов любой строки (столбца) равна определителю матрицы, полученной из данной заменой элементов этой строки (столбца) на числа b₁, b₂, ..., b_n.

10. Определитель произведения двух квадратных матриц одного размера равен произведению их определителей, т.е. С=AB, где C=AB .

Теорема Лапласа о разложении определителя по элементам строки или столбца

 Минором M_ij элемента a_ij матрицы n-го порядка A называется определитель матрицы (n-1)-го порядка, полученной из матрицы A вычеркиванием i-ой строки и j-го столбца.

 Алгебраическим дополнением A_ij элемента a_ij матрицы n-го порядка A называется его минор M_ij , взятый со знаком (-1)^i+j , т.е. A_ij=(-1)^i+j  M_ij .

Теорема Лапласа.

 Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:

A=a_i1A_i1+a_i2A_i2+...+a_inA_in(разложение по элементам i-ой строки);

A=a_1jA_1j+a_2jA_2j+...+a_njA_nj(разложение по элементам j-го столбца).

4. Понятие минора k-го порядка. Ранг матрицы (определение). Вычисление ранга матрицы с помощью элементарных преобразований

 Пусть задана матрица A размером mn и число k  min (m, n). Минором k-го порядка матрицы A называется определитель квадратной матрицы k-го порядка, полученной из матрицы A вычеркиванием каких-либо m-k строк и n-k столбцов.

Например, из матрицы A размером 34 можно получить миноры 1-го, 2-го и 3-го порядков..

 Рангом матрицы A называется наивысший порядок отличных от нуля миноров этой матрицы. Ранг матрицы A обозначается символом rang(A) или r(A).

Ясно, что: 1) r(A)  min (m, n); 2) r(A)=0  A - нулевая матрица;

3) если A - квадратная матрица n-го порядка, то r(A)=n  A0.

Определение ранга матрицы перебором всех миноров достаточно трудоемко. Для облегчения решения этой задачи используют преобразования, сохраняющие ранг матрицы.

 Элементарными преобразованиями матрицы называют следующие преобразования:

1) отбрасывание нулевой строки (столбца);

2) умножение всех элементов строки (столбца) на число, не равное нулю;

3) транспонирование матрицы;

4) изменение порядка строк (столбцов) матрицы;

5) прибавление к каждому элементу строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.

Теорема. Ранг матрицы при элементарных преобразованиях не изменяется.

Доказательство. Из свойств 1-4, 8 определителей следует, что при элементарных преобразованиях квадратных матриц их определители либо сохраняются, либо умножаются на число, не равное нулю. Таким образом, сохраняется наивысший порядок отличных от нуля миноров данной матрицы.

Обычно с помощью элементарных преобразований можно привести матрицу к ступенчатому виду, при котором легко определяется ранг матрицы.

 Матрица A называется ступенчатой, если она имеет вид ,

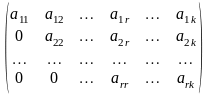где a_ii0 при i=1, 2, ..., r; rk.

Легко получить, что ранг ступенчатой матрицы равен r.