27. Общее уравнение прямой на плоскости, его исследование. Условия параллельности и перпендикулярности прямых

Определение 1. Уравнение с двумя переменными Ax + By + C = 0, где A и B не равны 0 одновременно, называется общим уравнением прямой на плоскости.

Теорема 1. Любая прямая на плоскости может быть задана общим уравнением.

Если В0, то 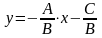, т.е. y=кх+b . При этом:

а) если А=0, то y=b;

б) если А=0 и С=0, то y=0;

в) если С=0, то y=кх .

Если В=0 и А0, то 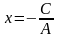, т.е. х=а - если С0 и х=0 - если С=0.

Теорема доказана.

Точка пересечения двух прямых A₁x + B₁y + C₁ = 0 и A₂x + B₂y + C₂ = 0 есть решение системы линейных уравнений

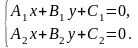
Пусть две прямые заданы уравнениями с угловыми коэффициентами y=к₁х+b₁ и y=к₂х+b₂, т.е. k₁=tg₁ и k₂=tg₂ , где ₁ и ₂ - углы наклона прямых к оси Ох.

Рассмотрим угол =₂-₁ - угол между данными прямыми. Тогда, по формуле тангенса разности, 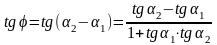, т.е. .

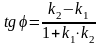Если прямые параллельны, то  = 0 , tg = 0.

Итак, условием параллельности двух прямых является равенство их угловых коэффициентов, т.е. k₁= k₂ .

Если прямые перпендикулярны, то  = /2 , ctg = 0.

Итак, условием перпендикулярности двух прямых является равенство k₁ k₂ =-1.

Замечание. Можно показать, что если две прямые заданы общими уравнениями A₁x + B₁y + C₁ = 0 и A₂x + B₂y + C₂ = 0, то:

условие параллельности прямых: ;

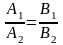условие перпендикулярности прямых: A₁A₂ + B₁B₂ = 0.

Кривые второго порядка, их общее уравнение. Нормальное уравнение окружности. Каноническое уравнение эллипса. Геометрический смысл параметров окружности и эллипса

Определение 1. Кривой второго порядка называется множество точек на плоскости, координаты которых удовлетворяют уравнению второго порядка с двумя переменными

Ax² + Bxy + Cy² + Dx + Ey + F = 0,

где A, B, C, D, E, F – действительные числа, причем A, B и C одновременно не равны нулю.

Определение 2. Уравнение Ax² + Bxy + Cy² + Dx + Ey + F = 0 называется общим уравнением кривой второго порядка.

В зависимости от коэффициентов A, B, C, D, E, F можно задать четыре типа невырожденных кривых: окружность, эллипс, гиперболу или параболу.

Рассмотрим уравнение, в котором B=0, коэффициенты A и C одновременно не равны нулю (A² + C²  0):

Ax² + Cy² + Dx + Ey + F = 0.

Для задания невырожденной кривой второго порядка (оси которой параллельны координатным осям) необходимо выполнение условий:

1. если A = C, то уравнение определяет окружность;

2. если AC>0, то уравнение определяет эллипс;

3. если AC<0, то уравнение определяет гиперболу;

4. если AC=0, то уравнение определяет параболу.

Определение 3. Окружностью называется геометрическое место точек плоскости, равноудаленных от фиксированной точки, называемой центром окружнсти.

Определение 4. Нормальным уравнением окружности радиуса R с центром в точке называется уравнение (x-x₀)² + (y-y₀)² = R².

В частности, уравнение окружности радиуса R с центром в начале координат имеет вид x² + y² = R² и называется каноническим уравнением окружности.

Определение 5. Эллипсом называется геометрическое место точек плоскости, сумма расстояний от которых до двух точек F₁ и F₂, есть величина постоянная, равная 2a, т.е. для любой точки M эллипса выполняется соотношение:

F₁M + F₂M = 2a.

Точки F₁(c,0) и F₂(-c,0) называются фокусами эллипса.

Определение 6. Каноническим уравнением эллипса (в канонической системе координат) называется уравнение .

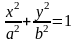В этом случае оси координат являются осями симметрии эллипса, а начало координат является его центром симметрии.

Вершинами эллипса являются точки A₁(a,0), A₂(-a,0), B₁(0,b) и B₂(0,-b).

Если параметры a и b удовлетворяют условию a > b, то они называются соответственно большой и малой полуосью эллипса.

Расстояние от начала координат до фокусов равно c и определяется соотношением .

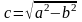Если параметры a и b удовлетворяют условию a < b, то фокусы эллипса расположены на оси Oy в точках F₁(0, c) и F₂(0, -c), а .

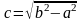Если центр эллипса смещен относительно начала координат в точку O(x₀,y₀), то уравнение эллипса будет иметь вид 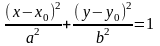и называться нормальным уравнением эллипса.

Приведение общего уравнения эллипса к нормальному виду проводится методом выделения полных квадратов по переменным x и y.

29. Канонические уравнения гиперболы и параболы, геометрический смысл их параметров. Уравнение асимптот гиперболы. График обратно пропорциональной зависимости и квадратного трехчлена

Определение 1. Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний от которых до двух точек F₁ и F₂, есть величина постоянная, равная 2a, т.е. для любой точки M гиперболы выполняется соотношение:

F₁M - F₂M = 2a.

Точки F₁(c,0) и F₂(-c,0) называются фокусами гиперболы.

Определение 2. Каноническим уравнением гиперболы (в канонической системе координат) называется уравнение .

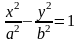В этом случае оси координат являются осями симметрии гиперболы, а начало координат является его центром симметрии.

Вершинами гиперболы являются точки A₁(a,0), A₂(-a,0), лежащие на оси Ox.

Параметры a и b называются соответственно действительной и мнимой полуосью гиперболы.

Расстояние от начала координат до фокусов равно c и определяется соотношением .

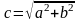Прямые 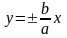называются асимптотами гиперболы.

Уравнение вида 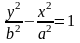также называется каноническим уравнением гиперболы.

В этом случае вершины A₁(0,b) и A₂(0,-b), а также фокусы F₁(0,c) и F₂(0,-c) гиперболы лежат на оси Oy.

Если центр гиперболы смещен относительно начала координат в точку O(x₀,y₀), то уравнение гиперболы будет иметь вид 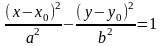или 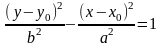и называться нормальным уравнением гиперболы.

Приведение общего уравнения гиперболы к нормальному виду проводится методом выделения полных квадратов по переменным x и y.

Определение 3. Параболой называется геометрическое место точек плоскости, равноотстоящих от данной точки (фокуса F) и данной прямой (директрисы):

MF = MN.

Определение 4. Каноническим уравнением параболы (если вершина параболы находится в начале координат) называется уравнение y² = 2px.

Точка 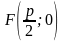называется фокусом параболы, а прямая 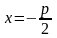- её директрисой.

При p > 0 ветви параболы направлены вправо, при p < 0 - влево.

Ось абсцисс является осью симметрии параболы.

Если в уравнении параболы поменять местами переменные x и y, то получим уравнение параболы x² = 2py с вершиной в начале координат и осью симметрии Oy.

При p > 0 ветви параболы направлены вверх, при p < 0 - вниз.

Если центр параболы смещен относительно начала координат в точку O(x₀,y₀), то уравнение параболы будет иметь вид (y-y_o)² = 2p(x-x₀) или (x-x_o)² = 2p(y-y₀) и называться нормальным уравнением параболы.

Приведение общего уравнения гиперболы к нормальному виду проводится методом выделения полного квадрата по переменной x или y.

25. Положительно и отрицательно определенная, знакоопределенная квадратичные формы. Критерии знакоопределенности квадратичной формы (через собственные значения ее матрицы и по критерию Сильвестра)

Определение 1. Квадратичная форма называется положительно (отрицательно) определенной, если при всех значениях переменных, из которых хотя бы одно отлично от нуля, выполняется неравенство

L(x₁, x₂, … , x_n)>0 (L(x₁, x₂, … , x_n)<0).

Теорема 1 (критерий определенности квадратичной формы). Для того чтобы квадратичная форма L=XAX была положительно (отрицательно) определена, необходимо и достаточно, чтобы все собственные значения_i матрицы A были положительны (отрицательны).

Теорема 2 (критерий Сильвестра). Для того чтобы квадратичная форма L=XAX была положительно определена, необходимо и достаточно, чтобы все главные миноры матрицы A были бы положительны, т.е.

, , …, .

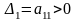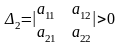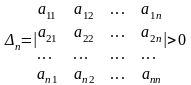Для того чтобы квадратичная форма L=XAX была отрицательно определена, необходимо и достаточно, чтобы знаки главных миноров матрицы A чередовались, начиная со знака «минус» для минора первого порядка, т.е.

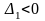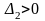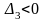, , и т.д.