
Классификация и критерии выбора методов
Конструирование вычислительных алгоритмов для конечно-разностного моделирования течений предполагает решение получающихся при этом взаимосвязанных систем линейных алгебраических уравнений. Поэтому естественно, что выбор численного метода их решения должен определять в значительной степени эффективность вычислительного комплекса в целом. Хотя методы решения сеточных уравнений можно рассматривать отдельно от физического содержания задач, следует отметить их взаимосвязь со структурой расчетного алгоритма. Действительно, с одной стороны, структура матрицы коэффициентов и типа разностного уравнения оказывают влияние на выбор метода его решения. С другой стороны, стремление добиться наибольшей эффективности вычислительного процесса стимулирует применение сложных трудоемких методов решения, которые требуют изменения самого расчетного алгоритма.
Следуя классификации, приведенной в работе [49], различают методы одновременного, или блочного, неявного решения систем разностных уравнений, последовательного, или явного, решения систем уравнений без учета взаимосвязи отдельных блоков и гибридные методы. Главная идея алгоритма расчета течений вязкой несжимаемой жидкости — сохранение взаимосвязи между уравнениями изменения количества движения и уравнением неразрывности, при этом уравнение для давления или уравнение для поправки давления явно не выводят и не решают. Вместо них конструируют вычислительный процесс одновременного определения скорости и давления, который автоматически использует взаимосвязь этих параметров течения. Систему разностных уравнений получают в рамках конечно-объемного подхода в сочетании с шахматной структурой расположения расчетных узлов. Для представления конвективных членов уравнения переноса используют противопоточную схему первого порядка аппроксимации. Записанную в блочной, матричной формулировке систему нелинейных алгебраических уравнений линеаризуют методом Ньютона и решают прямым численным методом обращения матриц.
Методы последовательного решения систем разностных уравнений сочетаются с положенной в основу распространенных расчетных алгоритмов концепцией расщепления по физическим процессам на конечно-разностном уровне [56,57].
Гибридные методы решения уравнений построены на основе частичного учета взаимосвязи исходных разностных уравнений. Например, в связанном виде рассматривают уравнения изменения количества движения или/и уравнения для характеристик турбулентности [43,58,61].
Как видно из представленной классификации численных методов, их выбор определяется во многом ресурсами имеющейся ЭВМ. Хотя тенденция совершенствования ЭВМ всех разновидностей указывает на рост производительности, однако ее еще не вполне достаточно, чтобы применять в расчетной практике прямые методы решения алгебраических уравнений. Отметим, что повышение точности расчетных процедур, как правило, также связано с задействованием дополнительных объемов памяти. Поэтому в подавляющем большинстве численных исследований используются различные итерационные методы решения разностных уравнений.
Из итерационных методов выделим методы линейного сканирования (LBL) и неявный метод переменных направлений (ADI) [39,52,59]. Метод линейного сканирования, известный в отечественной литературе как метод блочной итерации, основывается на сочетании скалярных трехточечных прогонок по линиям (метода скалярной прогонки) с итерационным методом Гаусса-Зайделя. Метод переменных направлений связан с расщеплением разностных параметров по координатным направлениям, причем при решении расщепленных уравнений также используется метод скалярной прогонки. Обе расчетные процедуры характеризуются высокой сходимостью, которая обеспечивается благодаря распространению влияния границ повсюду в расчетной области при завершении итерационного шага.
Итерационный процесс решения разностного уравнения заканчивается, когда удовлетворяется выбранный критерий сходимости для рассматриваемого разностного уравнения.
Изложим основные принципы наиболее широко распространенного численного метода решения системы уравнений на примере уравнений, описывающих двумерные нестационарные несжимаемые течения, — метода маркеров и ячеек (MAC) [39,53], разработанного Харлоу и Вэлчем.
Уравнения, описывающие двумерные нестационарные несжимаемые течения, имеют вид:
 (1.31)
(1.31)
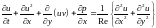 (1.32)
(1.32)
 (1.33)
(1.33)
Для
нестационарных течений требуется
определить начальные условия
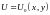 и
и
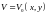 ,
удовлетворяющие уравнению (1.31). Граничные
условия на твердой поверхности заключаются
в отсутствии относительного движения
жидкости и твердого тела, что определяет
компоненты скорости. Граничные условия
для давления на твердой поверхности
задавать не надо. Так как компоненты
скорости определены на всей границе
области расчета, необходимо выполнить
условия
,
удовлетворяющие уравнению (1.31). Граничные
условия на твердой поверхности заключаются
в отсутствии относительного движения
жидкости и твердого тела, что определяет
компоненты скорости. Граничные условия
для давления на твердой поверхности
задавать не надо. Так как компоненты
скорости определены на всей границе
области расчета, необходимо выполнить
условия
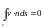 (1.34)
(1.34)
где
 - граница области расчета.
- граница области расчета.
Уравнение
(1.34) является глобальным выражением
(1.31) для всей расчетной области. На
входной границе ставится два граничных
условия, для скоростей
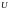 и
и
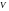 .
На выходной границе можно положить
.
На выходной границе можно положить
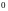 производные от скорости, граничные
условия для давления ставить не надо.
Поскольку в уравнение входят лишь
производные от давления, его величина
может быть определена в одной точке,
относительно которой будет осуществляться
отсчет давления.
производные от скорости, граничные
условия для давления ставить не надо.
Поскольку в уравнение входят лишь
производные от давления, его величина
может быть определена в одной точке,
относительно которой будет осуществляться
отсчет давления.
Процесс построения вычислительного решения системы (1.31-1.33) можно определить по пунктам:
исходные ДУЧП и граничные условия,
дискретизация,
СЛАУ,
алгоритм решения,
приближенное решение , , .
Первый этап (дискретизация) заключается в замене ДУЧП, описывающих непрерывный процесс, дискретной системой алгебраических уравнений, построенных для узлов расчетной сетки. Процесс построения расчетной сетки представляет для областей сложной конфигурации отдельную непростую задачу, однако, если границы совпадают с основными осями координат, то построение сетки очевидно. Рассмотрим элемент расчетной сетки для иллюстрации процесса дискретизации. Используется конечно-разностная аппроксимация производных по пространству, и разность вперед по времени [39,61].
Например, частные производные, входящие в уравнение (1.32), представляются так:
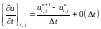

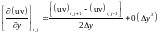 (1.35)
(1.35)
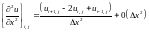
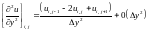

Для решения (1.32) может быть получен следующий явный алгоритм:
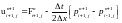 (1.36)
(1.36)
 (1.37)
(1.37)
Аналогично в дискретном виде представляется уравнение (1.33):
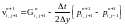 (1.38)
(1.38)
 (1.39)
(1.39)
В уравнения (1.36) и (1.38) давление
 входит неявно, однако
определяется до решения (1.36) и (1.38)
следующим образом. Уравнение неразрывности
(1.31) записывается в разностном виде:
входит неявно, однако
определяется до решения (1.36) и (1.38)
следующим образом. Уравнение неразрывности
(1.31) записывается в разностном виде:
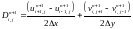 (1.40)
(1.40)
где
 - дилатация в ячейке
- дилатация в ячейке
Подстановка всех и из уравнений (1.36 - 1.38) позволяет представить (1.40) в виде разностного уравнения Пуассона для давления
При
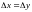
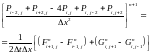 (1.41)
(1.41)
Т.о.
уравнения (1.41), записанные для каждого
узла расчетной сетки, представляют
собой СЛАУ, которая решается на каждом
шаге по времени итерационным, либо
прямым методом. После того, как
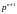 получено из решения (1.41), подстановка
этого значения в (1.36) и (1.38) позволяет
определить
получено из решения (1.41), подстановка
этого значения в (1.36) и (1.38) позволяет
определить
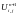 и
и
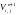 ,
которые автоматически удовлетворяет
уравнению неразрывности (1.40).
,
которые автоматически удовлетворяет
уравнению неразрывности (1.40).
Поскольку выражения (1.36) и (1.38) являются
формулами для определения
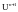 и
и
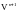 ,
имеется ограничение на максимальный
шаг по времени, связанное с устойчивостью
решения
,
имеется ограничение на максимальный
шаг по времени, связанное с устойчивостью
решения
 (1.42)
(1.42)
