
- •Понятие вероятности и классическое определение вероятности.
- •Некоторые элементы комбинаторики
- •Условная вероятность. Формула умножения вероятностей.
- •Формула Байеса
- •Аксиоматическое построение теории вероятностей
- •Последовательность независимых испытаний (схема Бернулли)
- •Случайные величины и функции распределения
- •Ф ункция распределения случайных величин
- •Плотность распределения случайной величины
- •Числовые характеристики случайных величин
- •Момент, дисперсия, среднеквадратичное отклонение
- •Зависимые и независимые случайные величины
- •Система произвольного числа случайных величин
- •Законы распределения и числовые характеристики функции случайных величин
- •Теоремы о числовых характеристиках
- •Закон распределения монотонной функции одного случайного элемента.
- •Предельные теоремы теории вероятностей
- •Закон больших чисел в форме теоремы Чебышева
- •Обобщённая теорема Чебышева и теорема Маркова
- •Характеристические функции
- •Основные свойства характеристических функций
- •Центральная предельная теорема для суммы одинаково распределённых слагаемых
- •Математическая статистика
- •Весовые характеристики статистического распределения
- •Доверительный интервал
- •Проверка статистических гипотез
- •Метод наименьших квадратов
Зависимые и независимые случайные величины
Случайная величина Y
называется независимой от случайной
величины X,
если закон распределения Y
не зависит от того, какое значение
приняла X
(т.е
![]() .
.
![]() .
.
Момент порядка
![]() ,
центральный момент:
,
центральный момент:
![]()
![]() .
Дли дискретного распределения
.
Дли дискретного распределения
![]()
![]() .
.
Посчитаем некоторые моменты:
![]() .
Аналогично
.
Аналогично
![]() .
.
![]() – корреляционный момент.
– корреляционный момент.
Пусть x и y
– независимые величины. Тогда
![]() и
и
![]()
![]() .
.
Две величины называют некоррелированными, если их корреляционный момент равен 0, иначе – коррелированными.
Система произвольного числа случайных величин
Функция распределения:
![]() .
.
Плотность распределения:
![]() .
.
Функция вероятности одной величины:
![]() ;
плотность вероятности одной величины:
;
плотность вероятности одной величины:
![]() .
.
Частная функция распределения:
![]() .
.
Условные вероятности:
![]() .
.
Числовые характеристики:
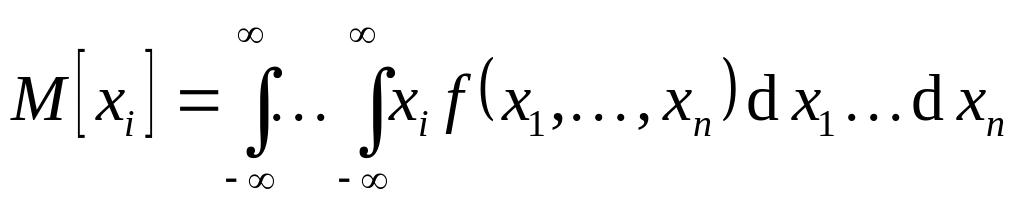 .
.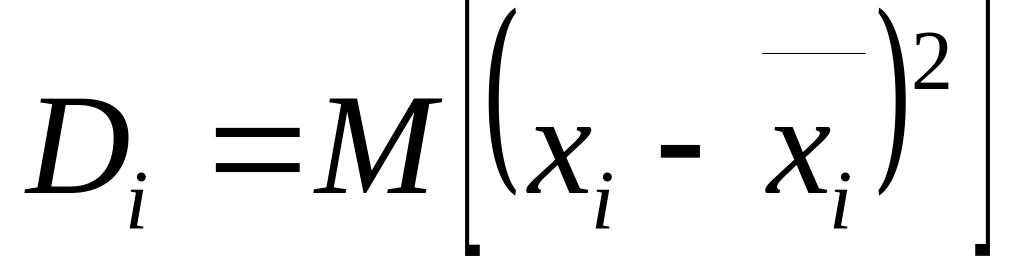 .
.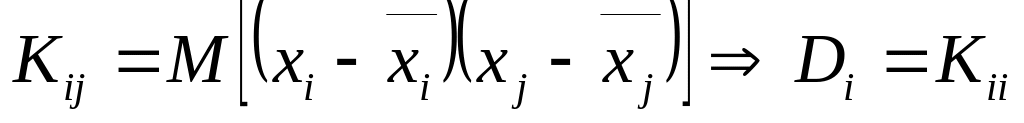 .
.Корреляционная матрица:
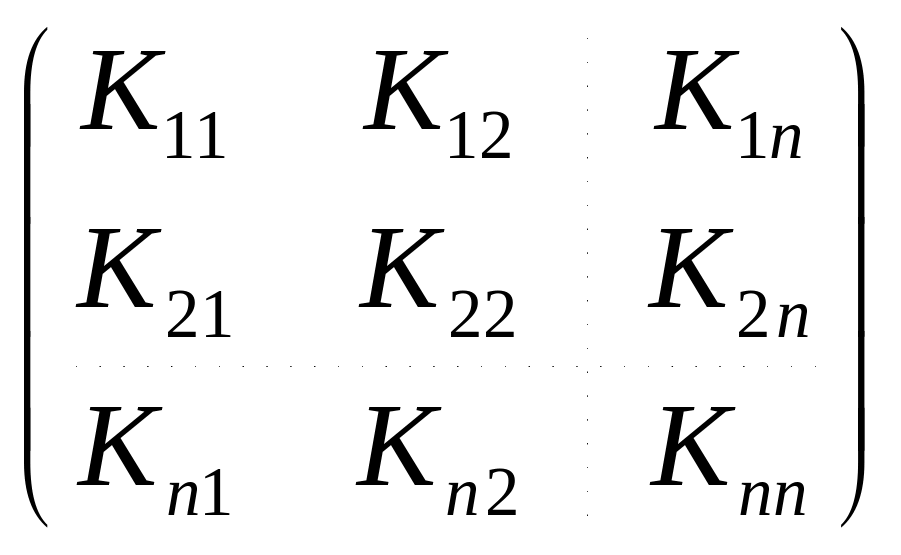 .
Эта матрица симметрична:
.
Эта матрица симметрична:
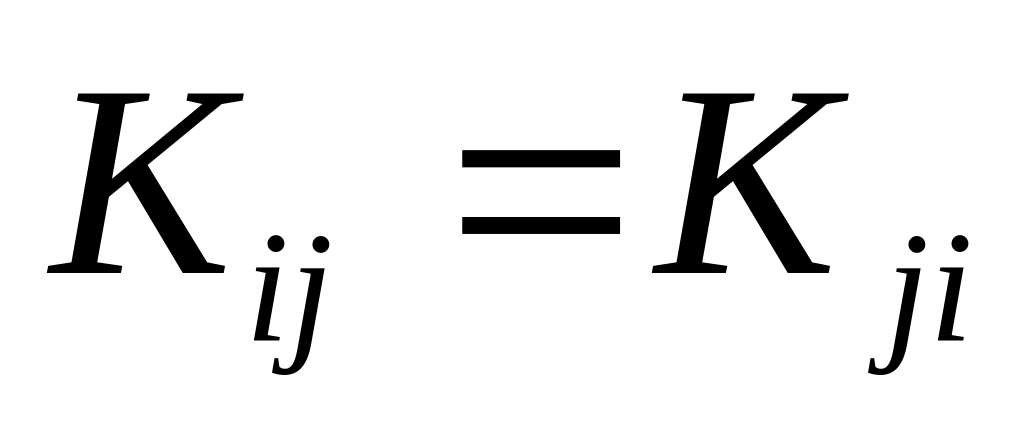 .
Если она диагональная, то система
независима.
.
Если она диагональная, то система
независима.
Нормальное распределение для двумерной
случайной величины:
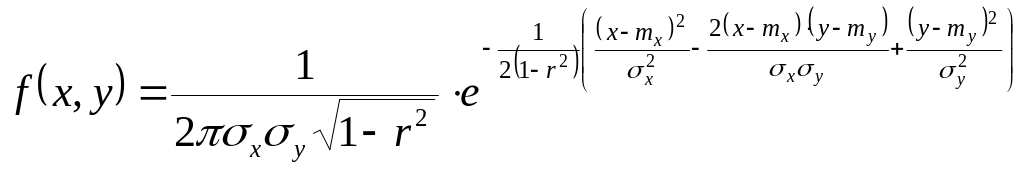 ,
где
,
где
![]() .
При этом
.
При этом
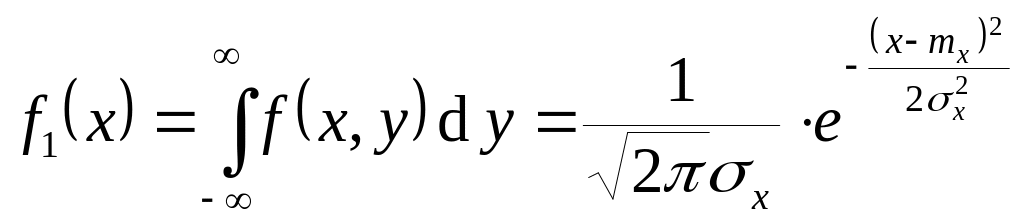 ,
,
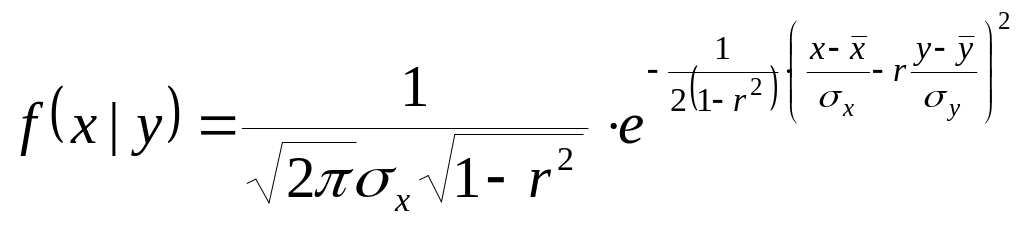 .
.
Законы распределения и числовые характеристики функции случайных величин
Будем рассматривать функцию одной
переменной:
![]() .
В случае дискретного x
задаётся ряд, т.е. каждому
ставится в соответствие вероятность
его выпадения
.
В случае дискретного x
задаётся ряд, т.е. каждому
ставится в соответствие вероятность
его выпадения
![]() .
Тогда по закону
.
Тогда по закону
![]() можно величинам
можно величинам
![]() поставить в соответствие те же вероятности
.
При этом их надо упорядочить в монотонно
возрастающем порядке и, если
поставить в соответствие те же вероятности
.
При этом их надо упорядочить в монотонно
возрастающем порядке и, если
![]() и
и
![]() ,
то
,
то
![]() .
.
Математической ожидание:
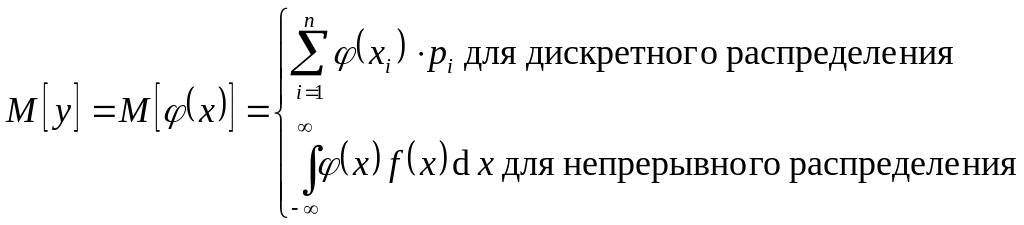 .
.
Теоремы о числовых характеристиках
, где C – не случайная величина.
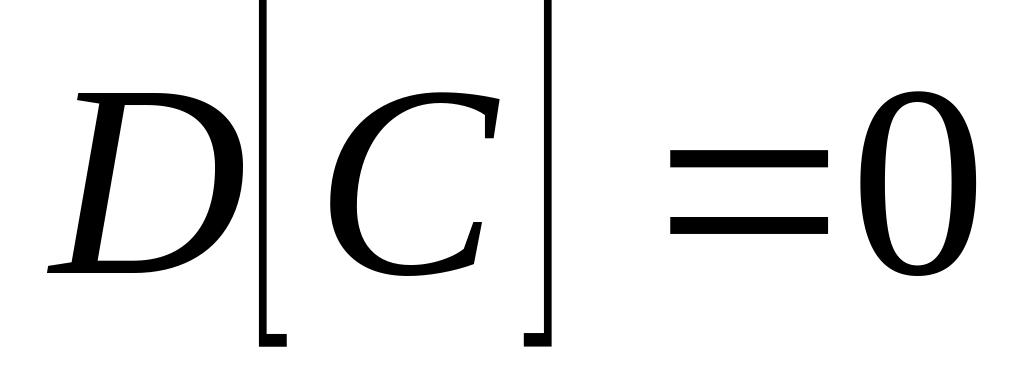 ,
где C
– не случайная величина.
,
где C
– не случайная величина..
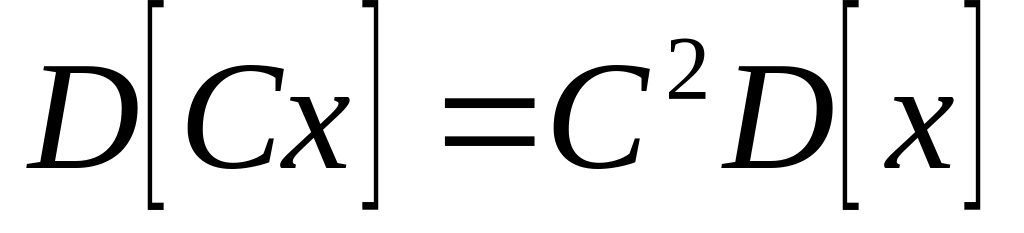 .
.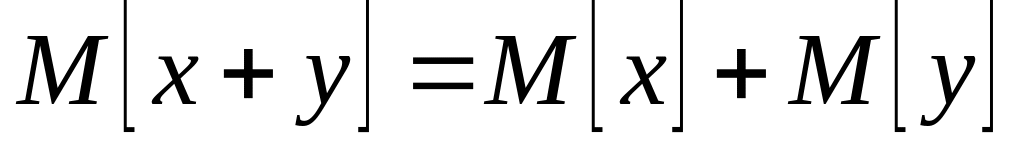 .
.
Доказательство последнего пункта:
![]()
![]() .
.
Аналогично
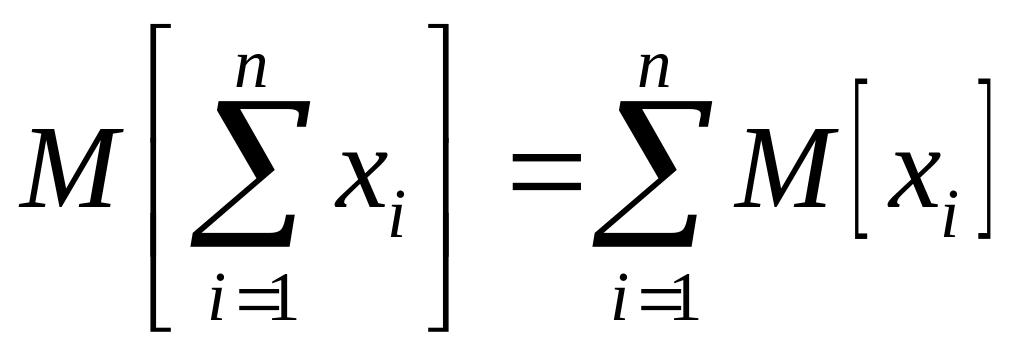 .
.
Если
 ,
то
,
то
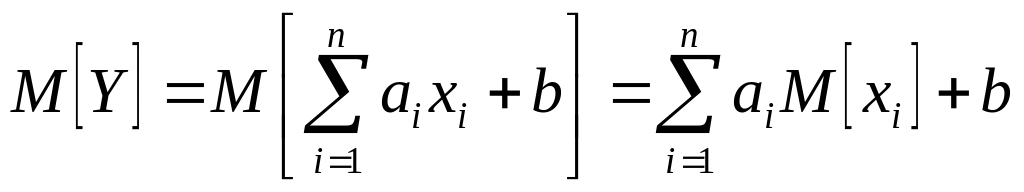 .
.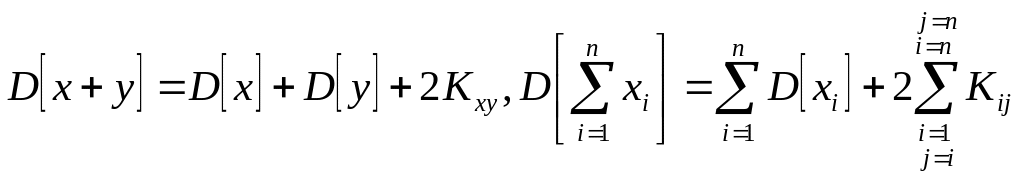 .
.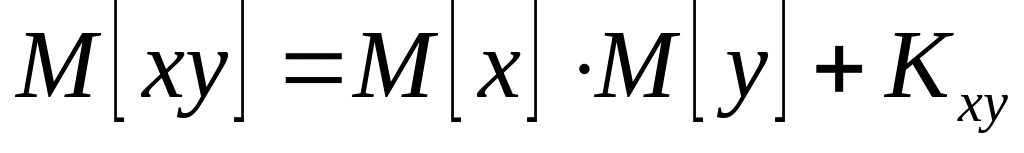 .
.
Закон распределения монотонной функции одного случайного элемента.
Пусть функция
![]() задана так:
задана так:
![]() , причём
, причём
![]() монотонно возрастает на
монотонно возрастает на
![]() .
Тогда Плотность распределения
.
Тогда Плотность распределения
![]() ,
где
,
где
![]() – функция распределения Y,
– функция распределения Y,
![]()
![]() ,
где
,
где
![]() – функция распределения величины X,
t – просто переменная
интегрирования. Т.к.
монотонна, то существует функция
– функция распределения величины X,
t – просто переменная
интегрирования. Т.к.
монотонна, то существует функция
![]() ,
обратная ей. Тогда
,
обратная ей. Тогда
![]() .
Если
.
Если
![]() убывает, то
убывает, то
![]() ,
ну а в общем случае
,
ну а в общем случае
![]() .
.
Закон распределения немонотонной функции одного случайного аргумента
Ф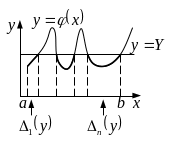 ункция
распределения
ункция
распределения
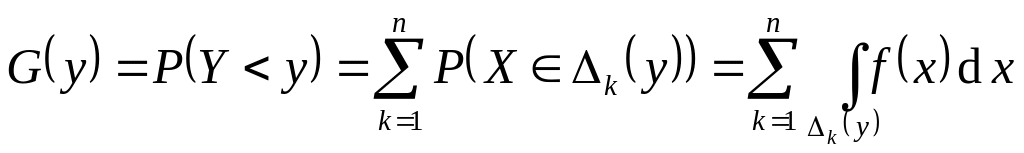 .
Плотность распределения
.
.
Плотность распределения
.
Закон распределения функции двух случайных величин
![]() .
Будем рассматривать более простой
случай
.
Будем рассматривать более простой
случай
![]() .
.
Ф ункция
распределения
ункция
распределения
![]() .
Плотность распределения
.
.
Плотность распределения
.
Закон распределения суммы двух случайных величин. Композиция законов распределения.
![]()
![]() .
Если x и y
– независимы, то
.
Если x и y
– независимы, то
![]()
![]() .
.
Если
![]() и
и
![]() – нормальные распределения, то
– нормальные распределения, то
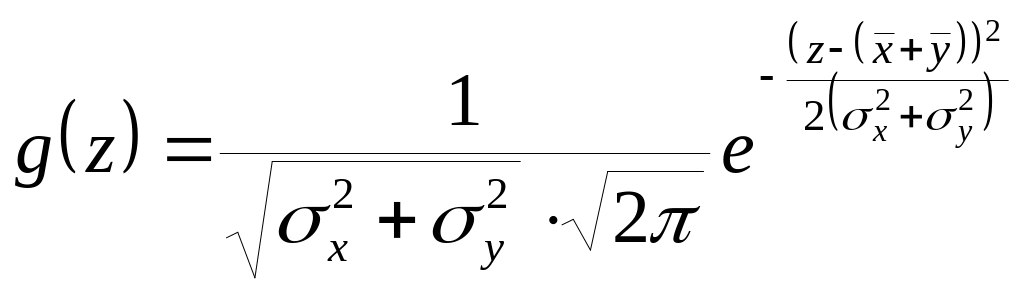 .
Видно, что распределение нормальное,
причём
.
Видно, что распределение нормальное,
причём
![]() .
.
Предельные теоремы теории вероятностей
Неравенство Чебышева: Каково
бы ни было
![]() ,
вероятность того, что X
отличается от своего математического
ожидания не меньше, чем на ,
ограничено сверху выражением
,
вероятность того, что X
отличается от своего математического
ожидания не меньше, чем на ,
ограничено сверху выражением
![]() .
.
![]()
![]() .
.
