
- •Понятие вероятности и классическое определение вероятности.
- •Некоторые элементы комбинаторики
- •Условная вероятность. Формула умножения вероятностей.
- •Формула Байеса
- •Аксиоматическое построение теории вероятностей
- •Последовательность независимых испытаний (схема Бернулли)
- •Случайные величины и функции распределения
- •Ф ункция распределения случайных величин
- •Плотность распределения случайной величины
- •Числовые характеристики случайных величин
- •Момент, дисперсия, среднеквадратичное отклонение
- •Зависимые и независимые случайные величины
- •Система произвольного числа случайных величин
- •Законы распределения и числовые характеристики функции случайных величин
- •Теоремы о числовых характеристиках
- •Закон распределения монотонной функции одного случайного элемента.
- •Предельные теоремы теории вероятностей
- •Закон больших чисел в форме теоремы Чебышева
- •Обобщённая теорема Чебышева и теорема Маркова
- •Характеристические функции
- •Основные свойства характеристических функций
- •Центральная предельная теорема для суммы одинаково распределённых слагаемых
- •Математическая статистика
- •Весовые характеристики статистического распределения
- •Доверительный интервал
- •Проверка статистических гипотез
- •Метод наименьших квадратов
Последовательность независимых испытаний (схема Бернулли)
Вероятность того, что в m
опытах из n произойдёт
какое-то событие
![]() .
.
Рассмотрим
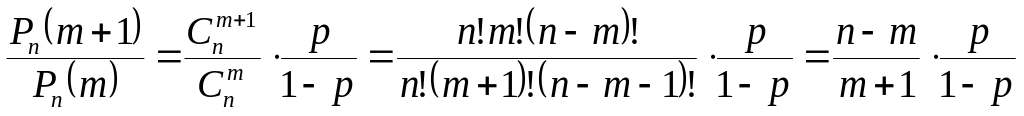 .
Очевидно, что
.
Очевидно, что
![]() .
Если
.
Если
![]() – целое число, то максимум достигается
в точках
– целое число, то максимум достигается
в точках
![]() и
и
![]() ,
иначе в точках
,
иначе в точках
![]() .
.
Если
![]() ,
то
,
то
![]() ,
т.е.
,
т.е.
![]() .
.
Локальная предельная теорема
Муавра-Лапласа: Если
вероятность наступления некоторого
события A
в n
независимых испытаний постоянна и
равна p,
то вероятность
![]() того, что в этих испытаниях событие A
наступит ровно m
раз, удовлетворяет при
того, что в этих испытаниях событие A
наступит ровно m
раз, удовлетворяет при
![]() соотношению
соотношению
![]() равномерно для
равномерно для
![]() ,
для которых
,
для которых
![]() находится в каком-либо конечном
интервале.
находится в каком-либо конечном
интервале.
![]() при
.
Далее,
при
.
Далее,
![]() .
Таким образом,
.
Таким образом,
![]()
![]() ,
где
,
где
![]()
![]() (т.к. при
(т.к. при
![]() )
)
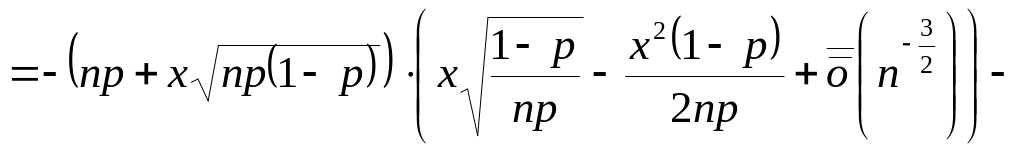
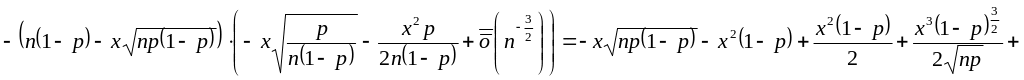
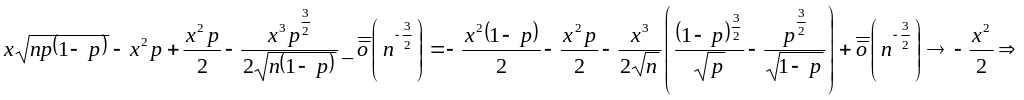
![]() и
и
![]() .
.
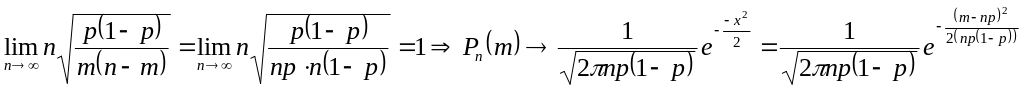 .
.
Вероятность того, что при n
испытаниях событие произойдёт от
![]() до
до
![]() раз:
раз:
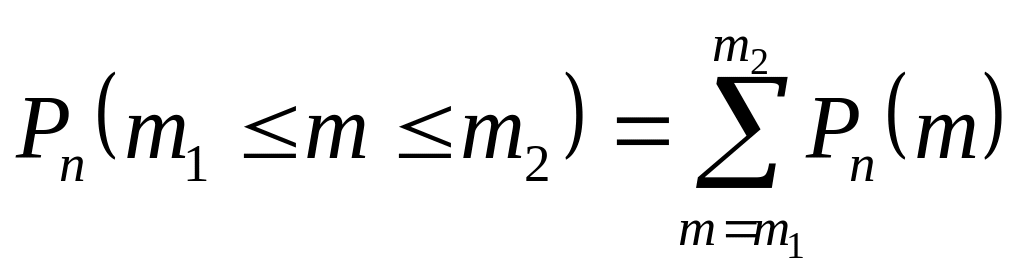 .
.
Интегральная теорема Муавра-Лапласа:
Если m
– число наступлений события при n
независимых испытаний, в каждом из
которых вероятность этого события –
p
![]() ,
то равномерно относительно a
и b
,
то равномерно относительно a
и b
![]() при
будет:
при
будет:
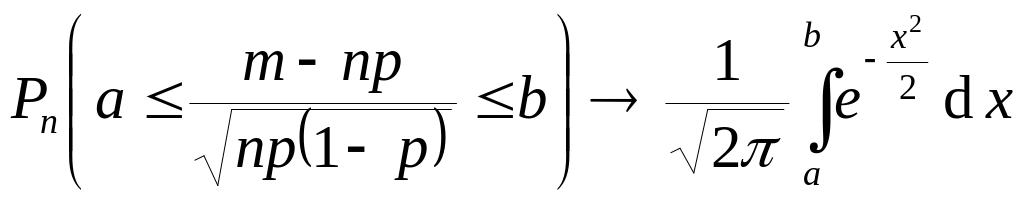 ,
где
,
где
![]()
![]() .
.
Из локальной предельной
теоремы Муавра-Лапласа следует, что
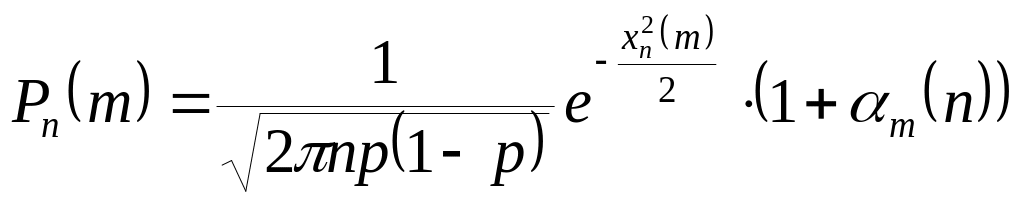 ,
где
,
где
![]() при
.
Рассмотрим разность
при
.
Рассмотрим разность
![]()
![]() .
Тогда
.
Тогда
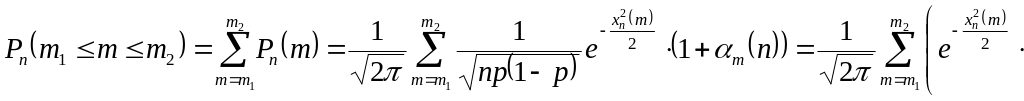
![]() .
Следовательно,
.
Следовательно,
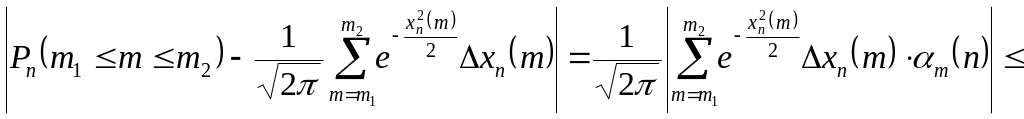
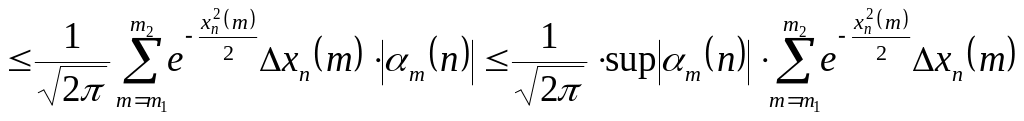 .
При
.
При
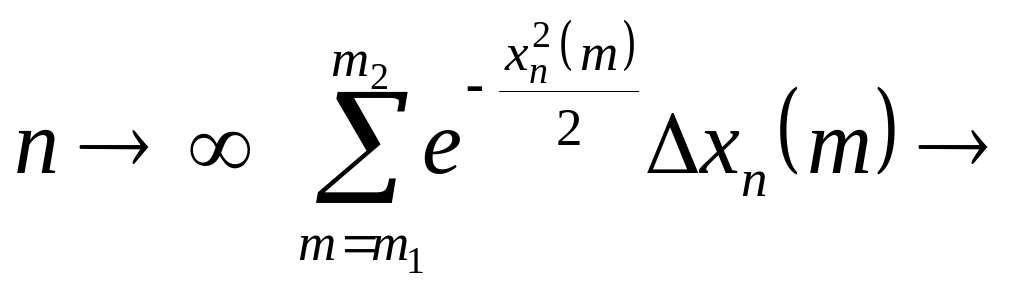
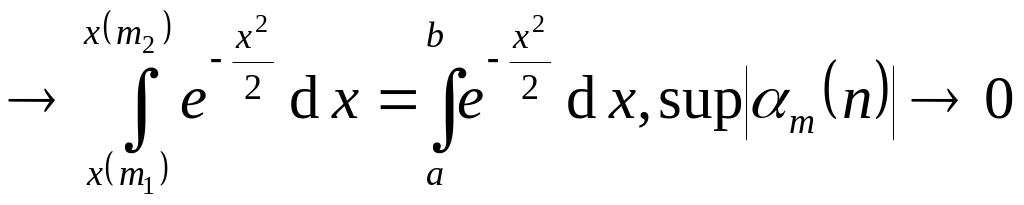 ,
следовательно,
,
следовательно,
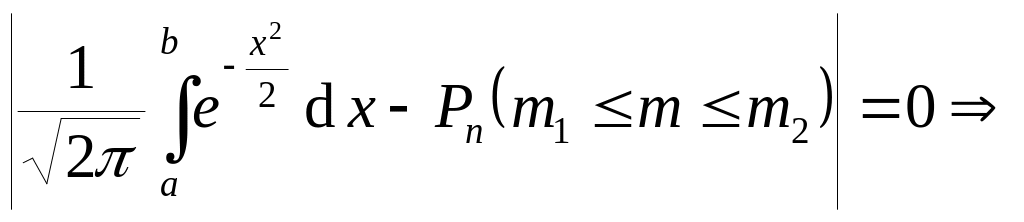
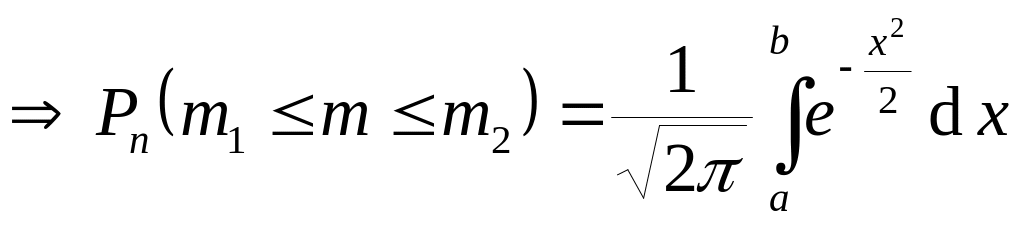 .
.
![]() – функция Гаусса.
– функция Гаусса.
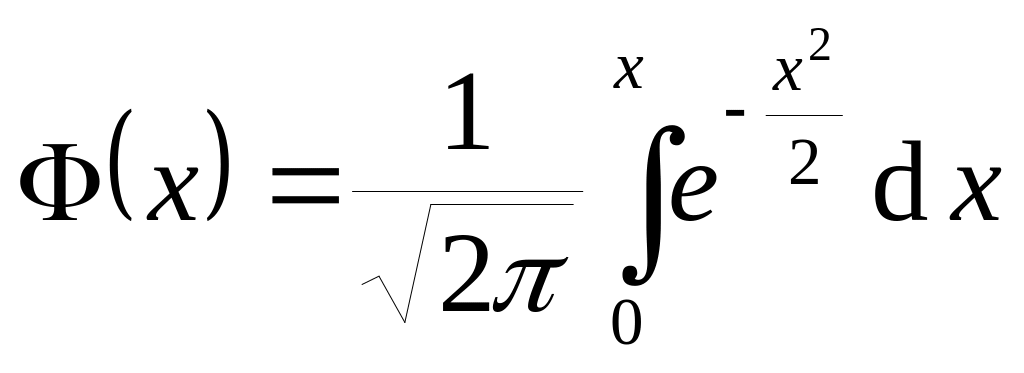 – функция Лапласа.
– функция Лапласа.
Таким образом,
![]() .
.
Для
![]() для
для
![]() будет
будет
![]() ,
где p
– вероятность появления события в
одном испытании,
,
где p
– вероятность появления события в
одном испытании,
![]() – классическая вероятность этого
события.
– классическая вероятность этого
события.
Рассмотрим
![]()
![]() (т.к.
(т.к.
![]() – нечётная функция) =
– нечётная функция) =
![]()
![]() ,
следовательно,
.
,
следовательно,
.
Эти формулы наиболее
эффективны при p
близком к
![]() или при очень
больших n.
или при очень
больших n.
Теорема Пуассона: Пусть
в схеме независимых испытаний величина
![]() остаётся постоянной при
.
Тогда для
остаётся постоянной при
.
Тогда для
![]() и
будет:
и
будет:
![]() – формула Пуассона.
– формула Пуассона.
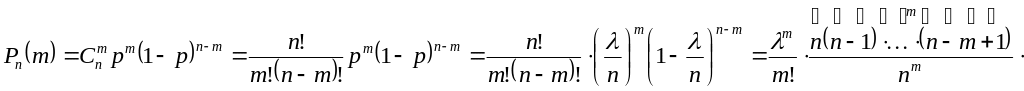
![]() .
.
![]() ,
следовательно, максимум получается
при
,
следовательно, максимум получается
при
![]() ,
т.е. наивероятнейшее количество удачных
опытов
,
т.е. наивероятнейшее количество удачных
опытов
![]() ,
если – дробное
и
,
если – дробное
и
![]() и
и
![]() ,
если – целое.
,
если – целое.
Случайные величины и функции распределения
Величина является случайной, если она в результате опыта может принять то или иное значение, которое заранее предсказать невозможно.
Функция, заданная на
пространстве событий
является случайной величиной (![]() ,
где
– элементарное событие).
,
где
– элементарное событие).
![]() – реализация случайной величины.
– реализация случайной величины.
X |
|
|
… |
|
P |
|
|
… |
|
Многоугольник (полигон) распределения:
Ф ункция распределения случайных величин
Функция распределения
– это вероятность того, что величина
X
попадёт в интервал
![]() (интегральный закон распределения).
Для дискретного X
(интегральный закон распределения).
Для дискретного X
![]() .
.
Свойства функции распределения:
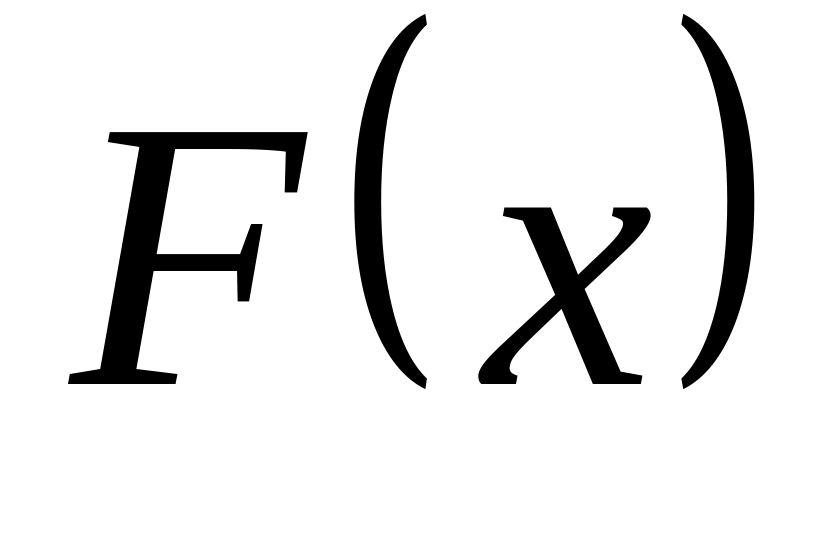 не убывает, т.е. если
не убывает, т.е. если
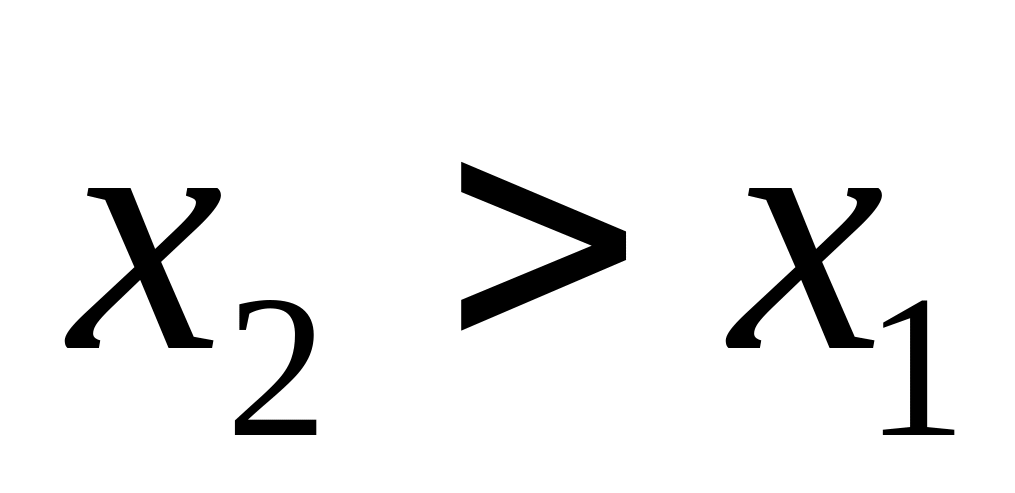 ,
то
,
то
 .
.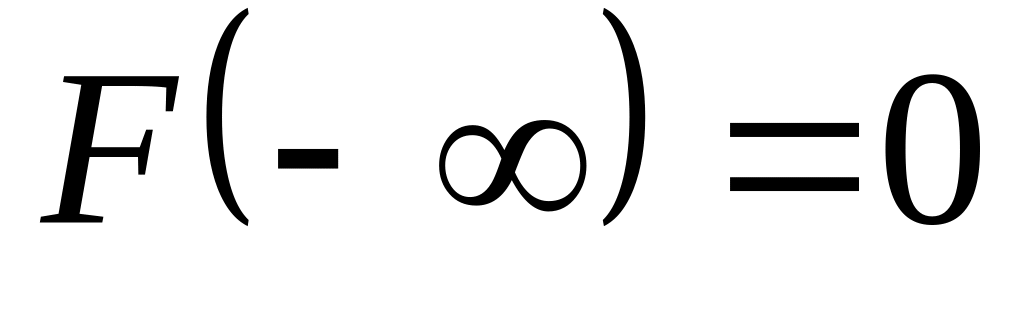 .
.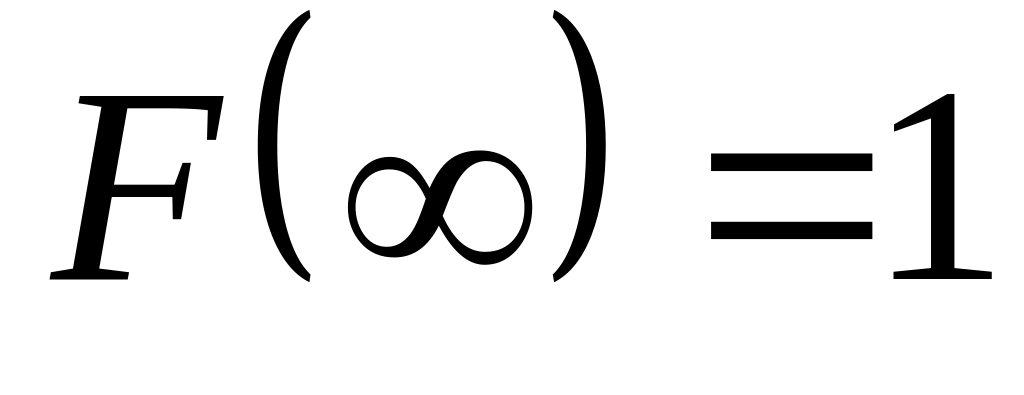 .
.
Вероятность попадания
случайной величины на заданный участок
![]() .
.
Пусть
![]() .
Тогда
.
Тогда
![]()
![]() ,
следовательно,
,
следовательно,
![]() .
.
