§ 4. Соленоидальное векторное поле и его свойства.
Уравнение неразрывности. Оператор Лапласа
Определение
1. Если векторное поле
таково, что в каждой его точке
,
то поле называется незаряженным или
соленоидальным.
Принимая во внимание механический смысл дивергенции векторного поля, нетрудно сделать вывод, что в соленоидальном поле нет источников и стоков.
Р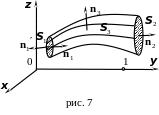
ассмотрим
теперь в соленоидальном векторном поле
некоторую замкнутую поверхность,
образованную векторной трубкой
и её двумя поперечными сечениями
и
.
Обозначим через
,
и
соответственно внешние нормали к
поверхностям
,
и
.
Так как поле вектора
соленоидально, то поток вектора
через замкнутую поверхность в силу
теоремы Остроградского равен нулю.
Поток
через рассматриваемую поверхность
равен сумме трёх потоков соответственно
через поверхности
,
и
, т.е.
.
Заметим, что поток через поверхность
векторной трубки
равен нулю, т.к. в каждой точке векторной
трубки вектор поля, соотнесенный этой
точке, касается поверхности этой трубки,
следовательно, его проекция на нормаль
к поверхности равна нулю.
Следовательно имеем:
.
Изменим
направление нормали
на противоположное, тогда получим
Следовательно, мы можем сделать вывод, что поток соленоидального векторного поля через поперечное сечение векторной трубки есть величина постоянная и не зависит от площади сечения. Эта величина называется напряжением векторной трубки.
Если
соленоидальное поле является полем
скоростей текущей несжимаемой жидкости
,
то мы имеем
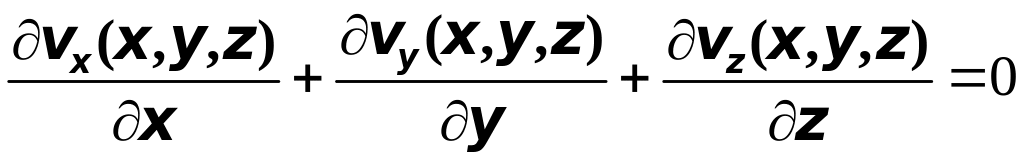(1)
Значит, если в пространстве, где течёт жидкость, нет ни источников, ни стоков, то проекции скоростей связаны соотношением (1), которое называется уравнением неразрывности.
Рассмотрим
теперь некоторое скалярное поле
и найдём его градиент:
.
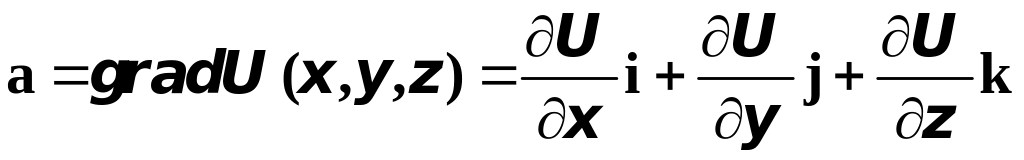Найдём далее дивергенцию векторного поля :
.
Определение
2. Оператор
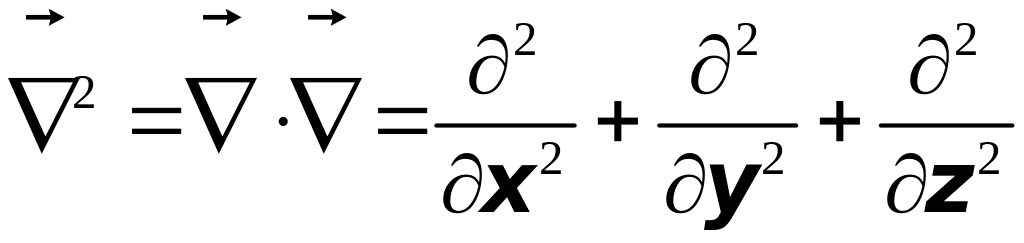называется оператором Лапласа
и обозначается символом
,
т.е.
,
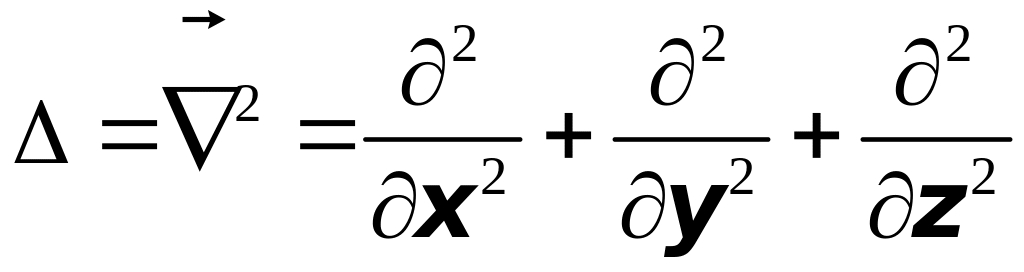а
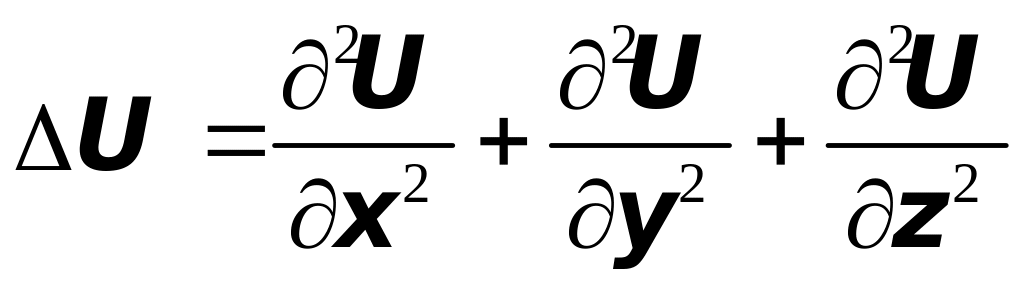
называется Лапласианом функции .
Определение 3. Если функция такова, что
,
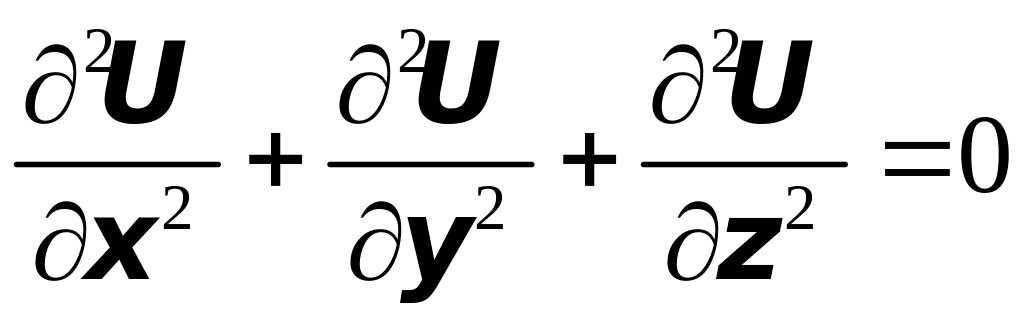т.е.
,
то функция называется гармонической.
Теорема. Для того, чтобы поле градиента какой-нибудь скалярной функции было соленоидальным, необходимо и достаточно, чтобы эта функция была бы гармонической.
Доказательство.
Необходимость. Поле градиента
соленоидально, т.е.
,
но
.
Значит,
,
а это означает, что функция
гармоническая.
Достаточность. Пусть функция - гармоническая, т.е.
,
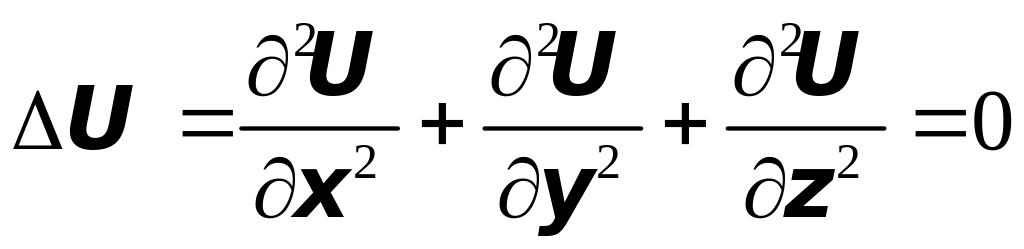но
,
а это и означает, что поле градиента
соленоидально.
§ 5. Циркуляция векторного поля по замкнутому контуру. Вихрь векторного поля. Векторная форма теоремы Стокса.
Пусть в поле вектора
лежит кривая
,
имеющая в каждой своей точке касательный
вектор
.
Обозначим
пр
.
Тогда криволинейный интеграл
называется линейным интегралом
(рис. 8). В том случае, когда кривая
замкнутая, интеграл называется циркуляцией векторного поля по замкнутому контуру.
Определение.
Вектор
называется вихрем векторного поля
и обозначается так:
.
Выразим
векторное произведение
через определитель:
.
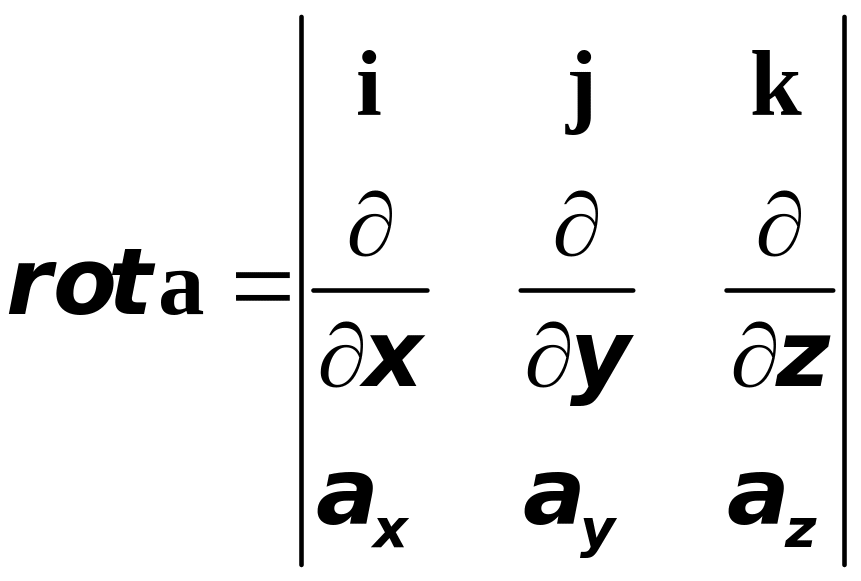Раскрыв этот определитель, получим такое выражение для вихря векторного поля:
.
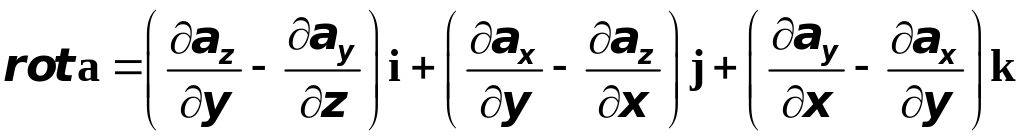Теорема.
Вихревое поле соленоидально, т.е.
.
Доказательство.
Заметим, что с очевидностью следует,
что
,
т.к. "векторы"
,
и
компланарны.
Докажем,
однако, эту теорему подробнее. Обозначим
,
тогда
,
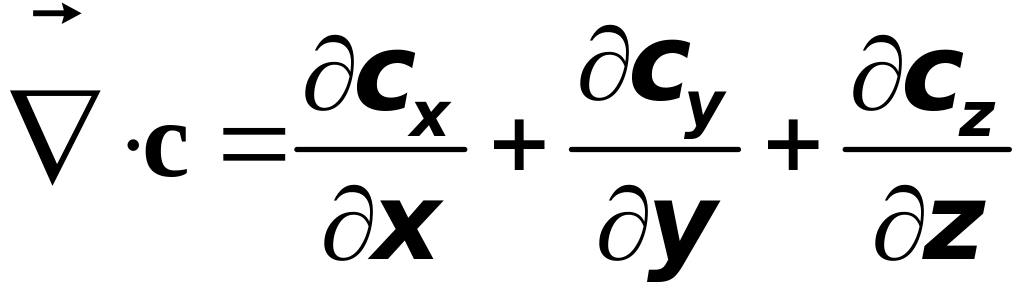но координаты вихря
,
,
.
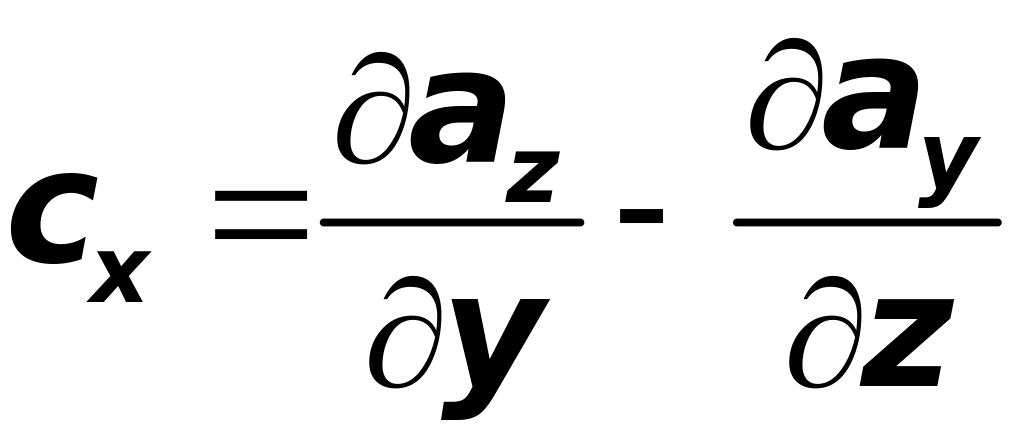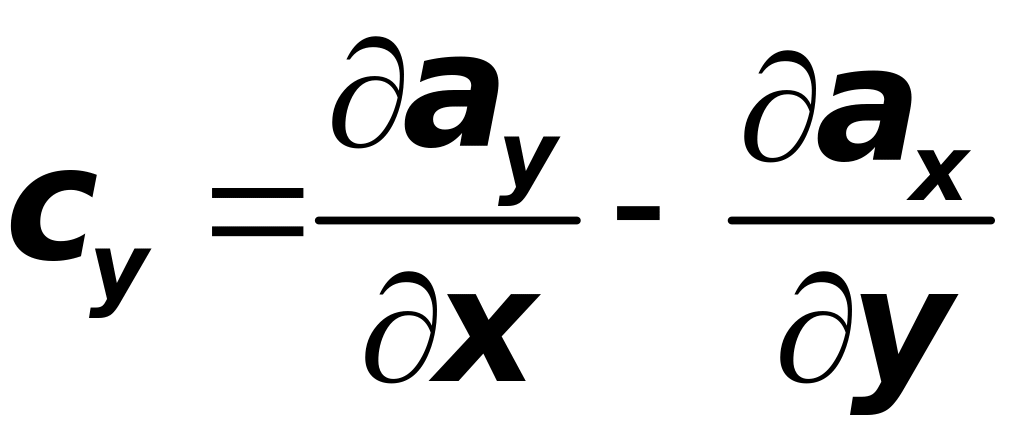Следовательно,
.
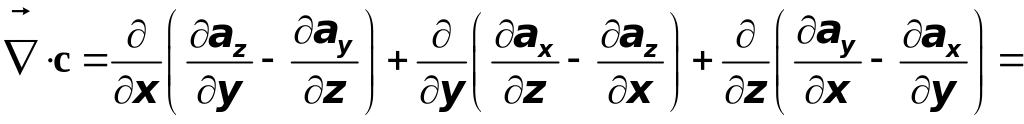
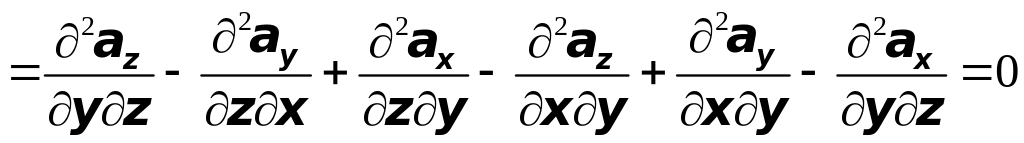Теорема доказана.
Заметим, что при доказательстве теоремы мы предположили существование вторых смешанных производных от проекций вектора и их непрерывность.
Допустим, что в поле вектора лежит замкнутый контур , имеющий в каждой своей точке касательную. Перекинем через контур двухстороннюю поверхность , имеющую в каждой своей точке нормаль к поверхности. При таких предположениях о контуре и поверхности справедлива доказанная ранее формула Стокса.
Докажем теперь векторную форму теоремы Стокса.
Теорема Стокса. (векторная форма).
Циркуляция векторного поля по замкнутому контуру равна потоку его вихря через поверхность, натянутую на этот контур.
Доказательство. Итак, пусть через замкнутый контур, обладающий указанными выше свойствами, перекинута (натянута) двухсторонняя поверхность . Рассмотрим циркуляцию векторного поля по замкнутому контуру : Ц= .
Пусть
касательный вектор
образует углы
,
и
с координатными осями
,
и
,
тогда
пр
=
.
Подставим
в выражение циркуляции, тогда получим
Ц=
или, принимая во внимание связь между
криволинейными интегралами первого и
второго рода, получим
Ц=
.
Воспользуемся теперь формулой Стокса:
.
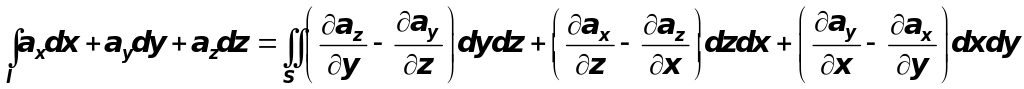При этом предполагается, что наблюдатель, у которого нормаль к поверхности проходит от ног к голове, обходит контур в таком направлении, что поверхность остаётся слева.
Нетрудно заметить, что в правой части последней формулы находится поток вихря векторного поля через поверхность , т.е. имеем
.
Теорема доказана.
Теорема 2. Вихрь векторного поля не зависит от выбора координатных осей.
Доказательство. Рассмотрим в поле вектора произвольное направление, заданное некоторым вектором .
П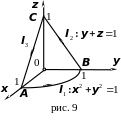
роведём
окружность
радиуса
,
плоскость круга
,
ограниченного контуром
,
перпендикулярна вектору
(рис. 9). По теореме Стокса
,
где
=пр
,
т.е.
.
Тогда по теореме о среднем имеем
,
где - некоторая "средняя точка", лежащая в круге . Тогда
.
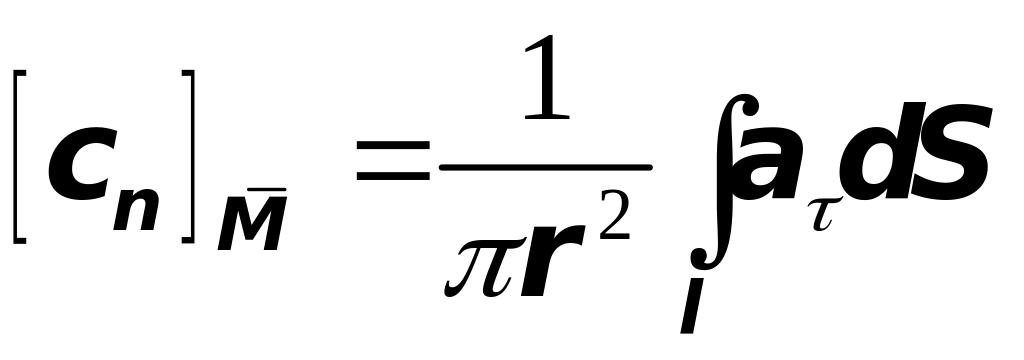Отсюда следует, что
,
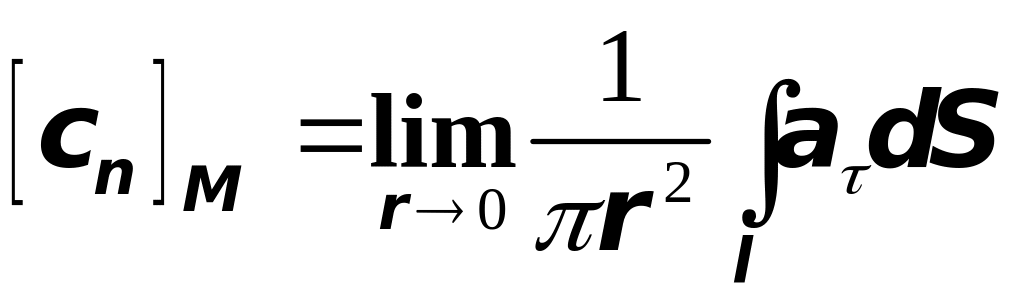где
- центр круга
.
Выражение в правой части равенства не
зависит от выбора координатных осей.
Значит
тоже от них зависит, а так как
- любое направление, то вектор
не зависит от выбора координатных осей.
Пример.
Вычислить циркуляцию векторного поля
по
линии пересечения конуса
с координатными плоскостями, лежащей в первом октанте, непосредственно и по теореме Стокса (рис. 10).
Решение.
1)
Непосредственное вычисление циркуляции.
Контур
можно разбить на три части:
,
и
,
лежащие в координатных плоскостях
,
и
соответственно, таким образом циркуляция
Ц=Ц1+Ц2+Ц3
, где
Ц1=
.
На кривой
:
,
.
Следовательно, Ц1=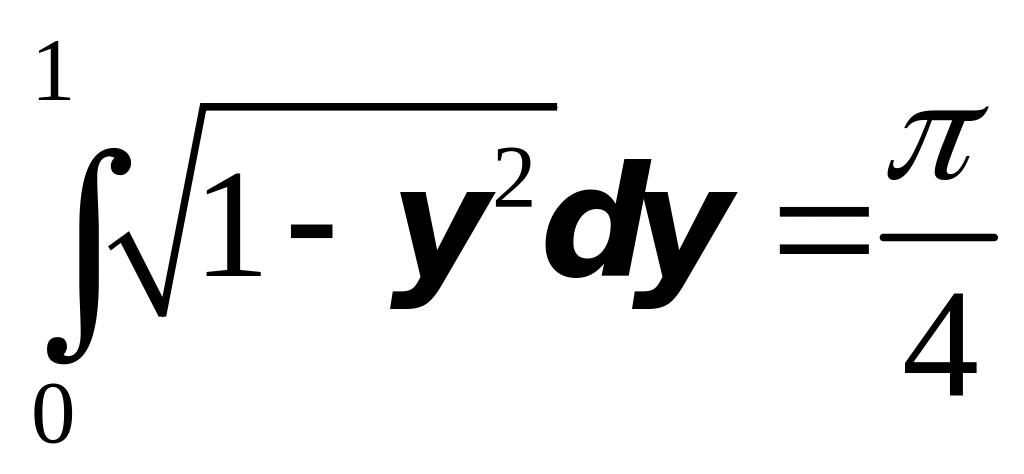
.
Далее
Ц2=
. На кривой
:
,
т.е.
Ц2=
.
И, наконец,
Ц3=
.
На кривой
:
,
,
,
,
следовательно, Ц3=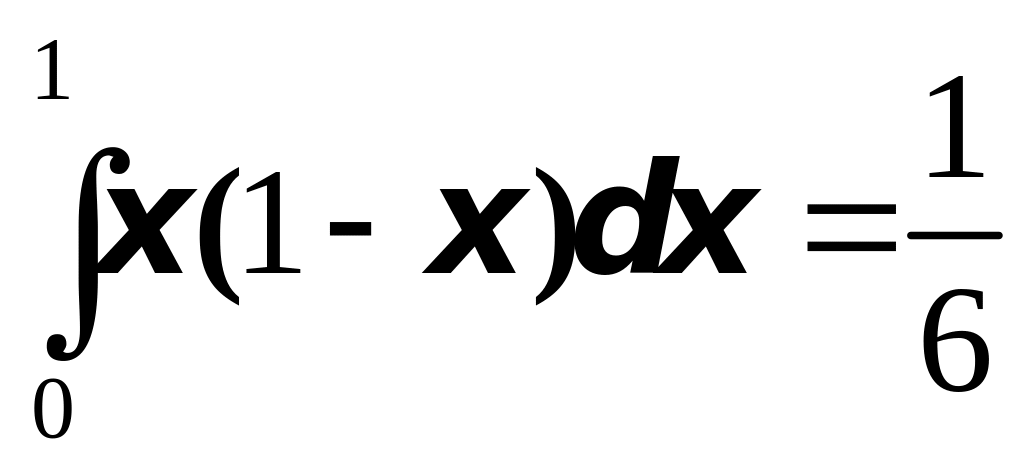
.
Окончательно
Ц=Ц1+Ц2+Ц3
=
.
2) Вычисление циркуляции по теореме Стокса:
Ц=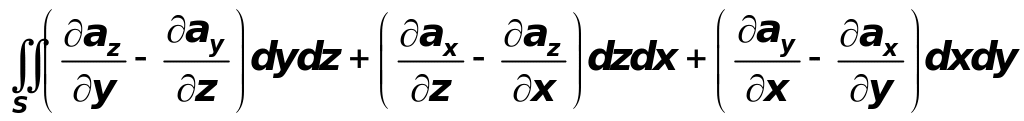
.
Подставим
сюда
,
получим
Ц1=
.
Перейдём в правой части к поверхностному
интегралу первого рода Ц=
,
где интеграл вычисляется по верхней
стороне поверхности
.
Уравнение
поверхности
:
,
следовательно,
,
,
;
;
;
.
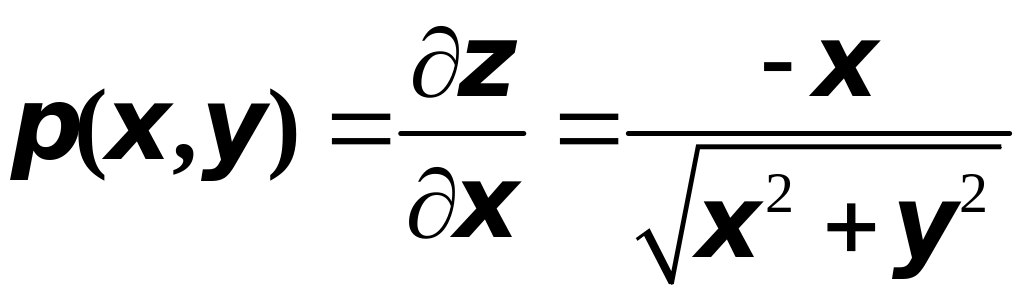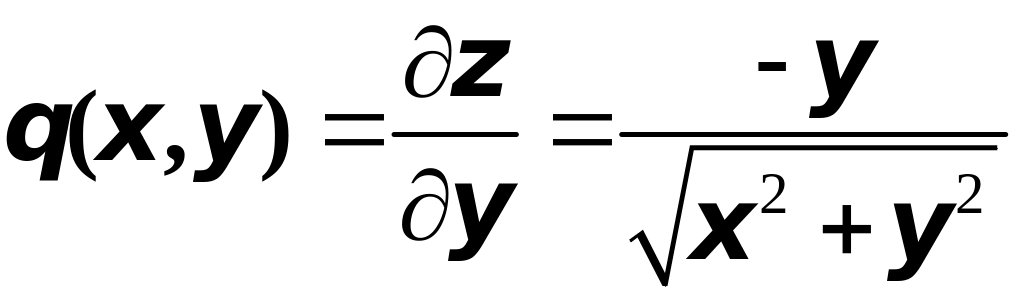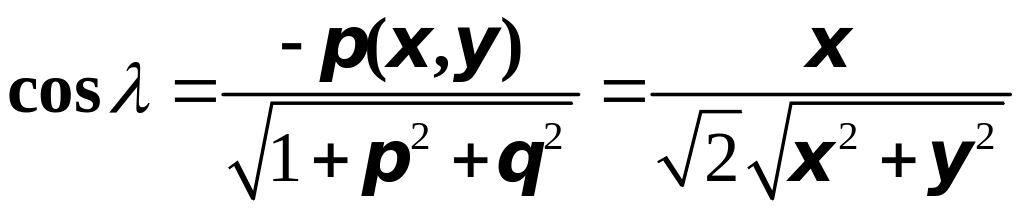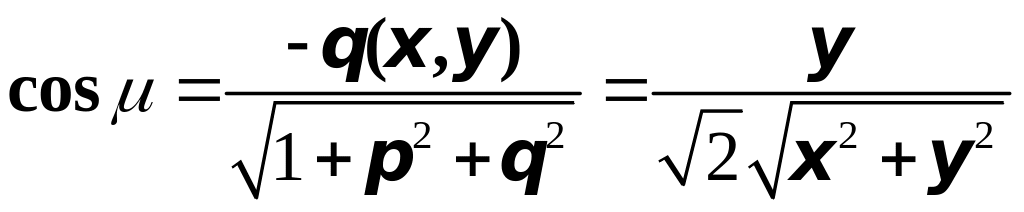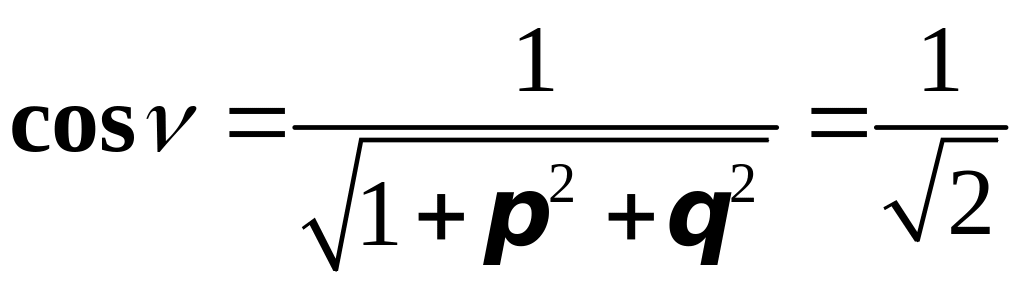Подставляя найденные значения в выражение для циркуляции, получим
Ц=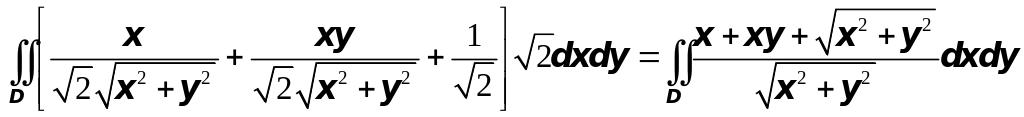
.
Перейдём к полярным координатам:
,
,
,
тогда
Ц=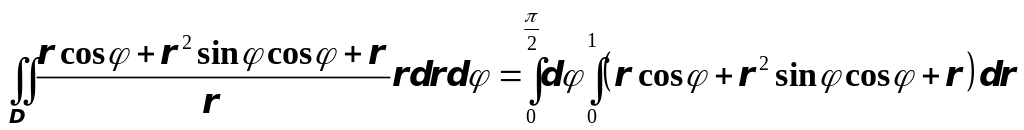
.
В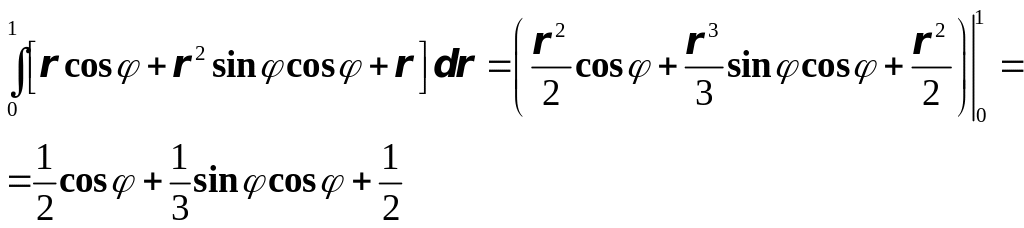
ычислим
внутренний интеграл:
ВН.=
тогда
Ц=
.